第01章 Spring概述

第01章 Spring概述

1.Spring概述

①Spring是一个开源框架

②Spring为简化企业级开发而生，使用Spring，JavaBean就可以实现很多以前要靠EJB才能实现的功能。同样的功能，在EJB中要通过繁琐的配置和复杂的代码才能够实现，而在Spring中却非常的优雅和简洁。

③Spring是一个IOC(DI)和AOP容器框架。

④Spring的优良特性

[1]非侵入式：基于Spring开发的应用中的对象可以不依赖于Spring的API

[2]依赖注入：DI——Dependency Injection，反转控制(IOC)最经典的实现。

[3]面向切面编程：Aspect Oriented Programming——AOP

[4]容器：Spring是一个容器，因为它包含并且管理应用对象的生命周期

[5]组件化：Spring实现了使用简单的组件配置组合成一个复杂的应用。在 Spring 中可以使用XML和Java注解组合这些对象。

[6]一站式：在IOC和AOP的基础上可以整合各种企业应用的开源框架和优秀的第三方类库（实际上Spring 自身也提供了表述层的SpringMVC和持久层的Spring JDBC）。

⑤Spring目前的版本

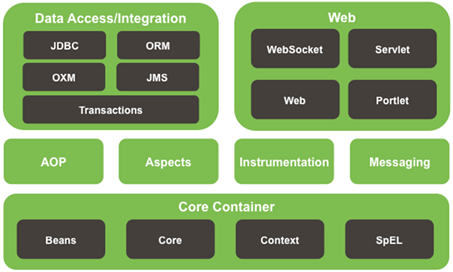
⑥Spring模块

2.安装Spring插件

①插件包：springsource-tool-suite-3.4.0.RELEASE-e4.3.1-updatesite.zip

②操作步骤：参照《参考资料：Spring插件安装图解.pptx》

3.搭建Spring运行时环境

①加入JAR包

[1]Spring自身JAR包：spring-framework-4.0.0.RELEASE\libs目录下

spring-beans-4.0.0.RELEASE.jar

spring-context-4.0.0.RELEASE.jar

spring-core-4.0.0.RELEASE.jar

spring-expression-4.0.0.RELEASE.jar

[2]commons-logging-1.1.1.jar

②根据需要创建Spring配置文件

4.HelloWorld

①目标：使用Spring创建对象，为属性赋值

②创建Student类

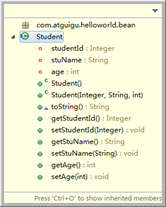
③创建Spring配置文件

<!-- 使用bean元素定义一个由IOC容器创建的对象 -->

<!-- class属性指定用于创建bean的全类名 -->

<!-- id属性指定用于引用bean实例的标识 -->

<bean id="student" class="com.atguigu.helloworld.bean.Student">

<!-- 使用property子元素为bean的属性赋值 -->

<property name="studentId" value="1001"/>

<property name="stuName" value="Tom2015"/>

<property name="age" value="20"/>

</bean>

④测试：通过Spring的IOC容器创建Student类实例

//1.创建IOC容器对象

ApplicationContext iocContainer =

new ClassPathXmlApplicationContext("helloworld.xml");

//2.根据id值获取bean实例对象

Student student = (Student) iocContainer.getBean("student");

//3.打印bean

System.out.println(student);

⑤验证：Spring在创建IOC容器对象时，就已经完成了bean的创建和属性的赋值。