[ZJOI2006]物流运输

题目描述

物流公司要把一批货物从码头A运到码头B。由于货物量比较大，需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线，以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在，有的时候某个码头会无法装卸货物。这时候就必须修改运输路线，让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情，会带来额外的成本。因此物流公司希望能够订一个n天的运输计划，使得总成本尽可能地小。

输入输出格式

输入格式：

第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数，m表示码头总数，K表示每次修改运输路线所需成本，e表示航线条数。接下来e行每行是一条航线描述，包括了三个整数，依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1，码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d，后面的d行每行是三个整数P(1<P<m)，a，b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物（含头尾）。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。

输出格式：

包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。

输入输出样例

输入样例#1：

5 5 10 8

1 2 1

1 3 3

1 4 2

2 3 2

2 4 4

3 4 1

3 5 2

4 5 2

4

2 2 3

3 1 1

3 3 3

4 4 5

输出样例#1：

说明

【样例输入说明】

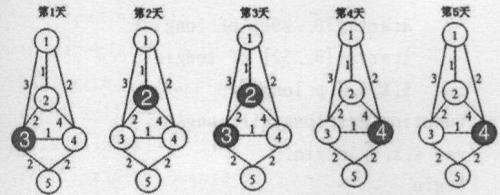
上图依次表示第1至第5天的情况，阴影表示不可用的码头。

【样例输出说明】

前三天走1-4-5，后两天走1-3-5，这样总成本为(2+2)3+(3+2)2+10=32。

_NOI导刊2010提高（01）

居然真的有图论套dp这种东西？？？

最开始觉得是最短路，思考了会儿发现不容易直接确定路径，因为如果每次刚好都是最短路上的点被封锁，那么交换路线的次数会很多，还不如选一条稍远的但是比较“安逸”的路线。

但是我们转眼一看诶$N,M$怎么都这么小？？？那么如果确定了一个时间段不换路径，那么这个时间段的路径就是最短路。对于一个时间点$i$，直接枚举上次交换是哪个时间点，用预处理出来的路径转移一下就行了。这类数据范围比较小的题目，可以多思考怎么通过暴力的枚举简化过程，暴力求解不容易快速求解的东西。

#include<bits/stdc++.h>

using namespace std;

int read()

{

    int x=0,w=1;char ch=getchar();

    while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}

    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();

    return x*w;

}

const int N=110;

int n,m,k,e,d,cnt,x,y,z;

int head[N],dis[N],p[110],a[110],b[110],c[110][110],dp[110];

bool vis[N];

struct node{

    int v,to,next;

}edge[N*N*2];

void add(int x,int y,int z)

{

    cnt++;edge[cnt].to=y;edge[cnt].v=z;edge[cnt].next=head[x];head[x]=cnt;

}

priority_queue<pair<int,int> >q;

void init(int l,int r)

{

    memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis));

    for(int i=1;i<=d;i++)

        if(l>b[i]||r<a[i]);else vis[p[i]]=1;

    q.push(make_pair(0,1));dis[1]=0;

    while(!q.empty())

    {

        int u=q.top().second;q.pop();

        if(vis[u])continue;vis[u]=1;

        for(int i=head[u];i;i=edge[i].next)

        {

            int v=edge[i].to;

            if(dis[v]>dis[u]+edge[i].v)

            dis[v]=dis[u]+edge[i].v,q.push(make_pair(-dis[v],v));

        }

    }

    c[l][r]=dis[m];

}

int main()

{

    n=read();m=read();k=read();e=read();

    for(int i=1;i<=e;i++)

    {

        x=read();y=read();z=read();

        add(x,y,z);add(y,x,z);

    }

    d=read();

    for(int i=1;i<=d;i++) p[i]=read(),a[i]=read(),b[i]=read();

    for(int i=0;i<=n;i++)for(int j=i;j<=n;j++)init(i,j);//,cout<<c[i][j]<<" ";

    memset(dp,0x3f,sizeof(dp));dp[0]=-k;

    for(int i=1;i<=n;i++)

        for(int j=0;j<i;j++)

            if(c[j+1][i]!=1061109567&&dp[j]!=1061109567)

                dp[i]=min(dp[i],dp[j]+(i-j)*c[j+1][i]+k);

    cout<<dp[n];

}