Paper慢慢读 - AB实验人群定向 Double Machine Learning

Hetergeneous Treatment Effect旨在量化实验对不同人群的差异影响，进而通过人群定向/数值策略的方式进行差异化实验，或者对实验进行调整。Double Machine Learning把Treatment作为特征，通过估计特征对目标的影响来计算实验的差异效果。

Machine Learning擅长给出精准的预测，而经济学更注重特征对目标影响的无偏估计。DML把经济学的方法和机器学习相结合，在经济学框架下用任意的ML模型给出特征对目标影响的无偏估计

HTE其他方法流派详见因果推理的春天-实用HTE论文GitHub收藏

核心论文

V. Chernozhukov, D. Chetverikov, M. Demirer, E. Duflo, C. Hansen, and a. W. Newey. Double Machine Learning for Treatment and Causal Parameters. ArXiv e-prints 文章链接

背景

HTE问题可以用以下的notation进行简单的抽象

Y是实验影响的核心指标
T是treatment，通常是0/1变量，代表样本进入实验组还是对照组，对随机AB实验$T \perp X$
X是Confounder，可以简单理解为未被实验干预过的用户特征，通常是高维向量
DML最终估计的是$\theta(x)$，也就是实验对不同用户核心指标的不同影响

\[
\begin{align}
Y &= \theta(x) T + g(X) + \epsilon &\text{where }E(\epsilon |T,X) = 0 \\
T &= f(X) + \eta &\text{where } E(\eta|X) = 0 \\
\end{align}
\]

最直接的方法就是用X和T一起对Y建模，直接估计$\theta(x)$。但这样估计出的$\theta(x)$往往是有偏的，偏差部分来自于对样本的过拟合，部分来自于$\hat{g(X)}$估计的偏差，假定$\theta_0$是参数的真实值，则偏差如下

\[
\sqrt{n}(\hat{\theta}-\theta_0) = (\frac{1}{n}\sum{T_i^2})^{-1}\frac{1}{\sqrt{n}}\sum{T_iU_i} +(\frac{1}{n}\sum{T_i^2})^{-1}(\frac{1}{\sqrt{n}}\sum{T_i(g(x_i) -\hat{g(x_i)})})
\]

DML模型

DML模型分为以下三个步骤

步骤一. 用任意ML模型拟合Y和T得到残差$\tilde{Y},\tilde{T}$

\[
\begin{align}
\tilde{Y} &= Y - l(x) &\text{ where } l(x) = E(Y|x)\\
\tilde{T} &= T - m(x) &\text{ where } m(x) = E(T|x)\\
\end{align}
\]

步骤二. 对$\tilde{Y},\tilde{T}$用任意ML模型拟合$\hat{\theta}$

$\theta(X)$的拟合可以是参数模型也可以是非参数模型，参数模型可以直接拟合。而非参数模型因为只接受输入和输出所以需要再做如下变换，模型Target变为$\frac{\tilde{Y}}{\tilde{T}}$, 样本权重为$\tilde{T}^2$

\[
\begin{align}
& \tilde{Y} = \theta(x)\tilde{T} + \epsilon \\
& argmin E[(\tilde{Y} - \theta(x) \cdot \tilde{T} )^2]\\
&E[(\tilde{Y} - \theta(x) \cdot \tilde{T} )^2] = E(\tilde{T}^2(\frac{\tilde{Y}}{\tilde{T}} - \theta(x))^2)
\end{align}
\]

步骤三. Cross-fitting

DML保证估计无偏很重要的一步就是Cross-fitting，用来降低overfitting带来的估计偏差。先把总样本分成两份：样本1，样本2。先用样本1估计残差，样本2估计$\hat{\theta}^1$，再用样本2估计残差，样本1估计$ \hat{\theta}^2$，取平均得到最终的估计。当然也可以进一步使用K-Fold来增加估计的稳健性。
\[
\begin{align}
sample_1, sample_2 &= \text{sample_split} \\
\theta &= \hat{\theta}^1 + \hat{\theta}^2 \\
\end{align}
\]

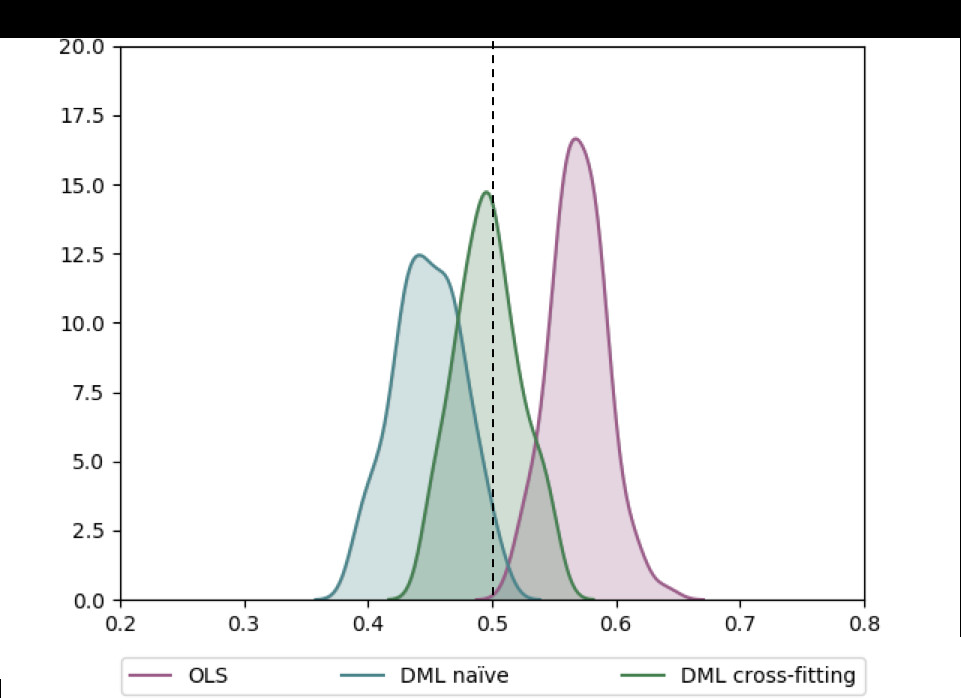
Jonas在他的博客里比较了不使用DML，使用DML但是不用Cross-fitting，以及使用Cross-fitting的估计效果如下

从GMM的角度来理解

Generalized Method of Moments广义矩估计 (GMM)在经济学领域用的更多，在论文里乍一看到moment condition琢磨半天也没想起来，索性在这里简单的回顾下GMM的内容。

啥是矩估计呢？可以简单理解是用样本的分布特征来估计总计分布，分布特征由$E((x-a)^K)$，样本的K阶矩来抽象，一阶矩就是均值，二阶原点矩就是方差。举几个例子吧～

例如，总体样本服从$N(\mu, \sigma^2)$就有两个参数需要估计，那么就需要两个方程来解两个未知数，既一阶矩条件$\sum{x_i}-\mu=0$和二阶矩条件$\sum{x_i^2} - \mu^2 - \sigma^2=0$。

再例如OLS，$Y=\beta X$可以用最小二乘法来求解$argmin (Y-\beta X)^2$，但同样可以用矩估计来求解$E(X(Y-\beta X))=0$。实则最小二乘只是GMM的一个特例。

那针对HTE问题，我们应该选择什么样的矩条件来估计$\theta$呢？
直接估计$\theta$的矩条件如下
$E(T(Y-T\theta_0-\hat{g_0(x)}))=0$
DML基于残差估计的矩条件如下
$E([(Y-E(Y|X))-(T-E(T|X))\theta_0](T-E(T|X)))=0$

作者指出DML的矩条件服从Neyman orthogonality条件，因此即便$g(x)$估计有偏，依旧可以得到无偏的$\theta$的估计。

参考材料&开源代码

V. Chernozhukov, M. Goldman, V. Semenova, and M. Taddy. Orthogonal Machine Learning for Demand Estimation: High Dimensional Causal Inference in Dynamic Panels. ArXiv e-prints, December 2017.
V. Chernozhukov, D. Nekipelov, V. Semenova, and V. Syrgkanis. Two-Stage Estimation with a High-Dimensional Second Stage. 2018.
Microsoft 因果推理开源代码 EconML
Double Machine Learning 开源代码 MLInference
https://www.linkedin.com/pulse/double-machine-learning-approximately-unbiased-jonas-vetterle/
https://www.zhihu.com/question/41312883