[总结]一些 DP 优化方法

目录

• 写在前面
• 矩阵快速幂优化
• 前缀和优化
• two-pointer 优化
• 决策单调性对一类 1D/1D DP 的优化
  • \(w(i,j)\) 只含 \(i\) 和 \(j\) 的项——单调队列优化
    • 单调队列优化多重背包
  • \(w(i,j)\) 只含 \(i,j\) 和 \(ij\) 的项——斜率优化
  • 决策单调性适用的原理——四边形不等式与决策单调性
  • \(w(i,j)\) 满足四边形不等式的更一般的情形——分治/二分数据结构
    • 分治
    • 二分+数据结构
  • 四边形不等式的一点补充
• 四边形不等式的另一单调性优化
• 不满足决策单调性的斜率优化
• 带权二分优化（DP 凸优化）
• 数据结构优化
• 参考文献

写在前面

1. ACM 训练（复习）的时候重新学习了一下常见的 DP 转移的优化技巧，在学习的同时也有一些自己的理解，便一并总结在这。
2. 本文成文前阅读或参照了许多大佬的博客，这些将附在文末参考文献中。
3. 若文章中出现错误，烦请告知。感谢您的造访。

矩阵快速幂优化

主要是利用矩阵快速幂来优化一些线性递推问题。高维 DP 如果某一维状态较少也可以用矩乘优化。

这个比较普及不细讲，但是注意图的邻接矩阵也是可以用来矩阵加速的。

例题

• [HNOI 2011]数学作业
• [POJ 3233]Matrix Power Series
• [USACO 07NOV]Cow Relays

前缀和优化

当转移碰到类似于 \(f_i=\sum\limits_{l\leq j\leq r}g_j\) 时，我们可以对 \(g\) 做一个前缀和，之后两端点差分即可。同时，其中求和式可换成 \(\min\) 或 \(\max\)，不过优化的适用条件更为苛刻。

另外多维 DP 有时也能用到前缀和优化，关键就是找到转移式有哪一个部分是只随着一个枚举变量变化而变化的，通过交换枚举顺序可以做到用前缀和优化。另外，要注意取的究竟是“前缀”还是“后缀”或是中间某两个端点，计算端点的值的时候要考虑交换 for 对循环范围的影响。[HEOI 2013]SAO这题可能会让你对这部分有充分了解。

例题

• [HAOI 2009]逆序对数列
• [HEOI 2013]SAO

two-pointer 优化

也就是双指针优化。最常见的双指针优化是“尺取法”。双指针优化，大概就是一个端点移动时，取最优值时另一个端点是单调移动的。

例如，我想在一个有序数组 \(a\) 中找到两个数 \(a_i,a_j(i<j)\)，使得 \(a_j-a_i\leq C\) 且 \(a_j-a_i\) 最大。那么我们移动左端点 \(i\) 时，只需找到 \(a_j\leq C+a_i\) 的最大值即可。因为数组单调，\(j\) 也可以单调移动。当然根据题目不同，指针移动的方向是不同的，但是本质上就是固定其中一个端点，最优性地移动另一个端点。

这样我们就能省去其中一维的枚举，起到优化复杂度的目的。

例题

• [HNOI 2017]大佬
• [NOI 2011]NOI 嘉年华

决策单调性对一类 1D/1D DP 的优化

这里 xD/yD DP 意思是状态数有 \(n^x\) 种，每个状态的转移有 \(n^y\) 种的 DP。而 1D/1D DP 通常长这样
\[
f_i = \min(\max)\{f_j+w(i,j)\}
\]

而决策单调性是指，对于两个决策点 \(j\) 与 \(k(j<k)\)，如果对于状态 \(i\)，决策 \(​k\) 优于 \(​j\)，那么对于 \(​\forall i′(i′>i)\) 都有 \(k\) 优于 \(j\)，即从 \(k\) 转移一定更优，\(j\) 一定不再会成为最优决策，决策是单调的，和上文提到的双指针优化有点类似。

未经优化的 1D/1D DP 通常复杂度是 \(O(n^2)\)。这部分将围绕 \(w(i,j)\) 不同的性质分情况来讨论不同的优化方法。注意多维 DP 中某一维可能也是 1D/1D 的，那么这一维也是可以单独拿出优化的，因此下面只讨论纯粹的 1D/1D DP。

在这里，笔者叙述的思路是先讨论几个常见的优化方法，之后再引出其共同点以及一些拓展。内容有一定连续性，不建议跳跃阅读。

\(w(i,j)\) 只含 \(i\) 和 \(j\) 的项——单调队列优化

我们不妨将转移写成 \(f_i = \min(\max)\{f_j+a[i]+b[j]\}\)，以 \(\min\) 为例。

因为 \(a[i]\) 与 \(j\) 无关，实际上转移就是 \(f_i = \min\{f_j+b[j]\}+a[i]\)。那么我们只要找到 \(\min\) 括号内最小的即可。

若 \(1\leq j<i\)，请移步前缀和优化。而一般来说 \(j\) 都是在一个移动的区间取值的，并且随 \(i\) 移动而移动，我们设为 \([l_i,r_i]\)，\(l_i,r_i\) 单调不减。

那么我们就只需维护一个单调递增的单调队列，单调队列中存放 \(f_j+b[j],j\in[l_i,r_i]\)，并且对应的下标也单调递增。对于每一个 \(i\)，我们先将新增区间部分从队尾加入单调队列，因为需要维护单调性，如果尾部的元素大于需要加入的元素直接舍弃，因为它不可能成为最优决策点。接着考虑队首元素是否在可转移区间内，若不满足就一直出队直到找到一个满足条件的队首。那么此时的队首是 \([l_i,r_i]\) 中的最小值，更新 \(f_i\)。

例题

• [Codeforces 922E]Birds
• [POI 2014]PTA-Little Bird
• [SCOI 2010]股票交易
• [NOI 2005]瑰丽华尔兹

单调队列优化多重背包

一般的多重背包方程式通常是 \(f_{i}\) 表示容积为 \(i\) 时的最大价值。转移大概是（其中物品种数 \(n\)，容积 \(v\)，第 \(i\) 个物品有 \(c_i\) 个，体积 \(v_i\)，价值 \(w_i\)）

for (int i = 1; i <= n; i++)
    for (int k = 1; k <= c[i]; k++)
        for (int j = v; j >= v[i]*k; j--)
            f[j] = max(f[j], f[j-v[i]*k]+w[i]*k);

显然复杂度是 \(O(v\sum c_i)\)。一种可行的优化方法是二进制分解，大致思路是将每种物品的个数基于二进制分解为 \(O(\log c_i)\) 个不同的物品，再用这些分解后的物品做 01 背包，复杂度 \(O(vn\log c)\)。

另一种方案就是利用单调队列来优化。大致思路就是考虑放第 \(i\) 种物品时，我们将 \(f\) 中模 \(v_i\) 同余 \(x,x\in[0,v_i)\) 的下标拿出来拼在一起记作 \(g\)，即 \(g_j=f_{(j-1)v_i+x}\) 。那么实际上，原方程 \(f_j = \max\limits_{1\leq k\leq c_i}\{f_{j-v_i\times k}+w_i\times k\}\) 等价于 \(g_j = \max\limits_{1\leq k\leq c_i}\{g_{j-k}+w_i\times k\}=\max\limits_{j-c_i\leq a<j}\{g_a+w_i\times (j-a)\}\)。这个是可以单调队列优化的。综上复杂度变成了 \(O(vn)\)。

例题就不给了，随便找个多重背包模板改了交上去就好了。

\(w(i,j)\) 只含 \(i,j\) 和 \(ij\) 的项——斜率优化

将转移写成 \(f_i = \min(\max)\{a[i]\times b[j]+c[i]+d[j]\}\)，式子中不含 \(f_j\) 是因为 \(f_j\) 可能参与了 \(b[j]\) 和 \(d[j]\) 的运算，为了方便表达就直接将 \(f_j\) 隐去了，不过这是不影响后续讨论的。同时，这种形式的决策单调性的优化 \(a,b\) 需要满足一些条件，这里以 \(a\) 单调递减，\(b\) 单调递增为例，至于原因以及其他适用条件，在之后的讨论会给出。还是以 \(\min\) 为例。

那么现在需要的就是对于每个 \(i\)，找到最优决策点 \(j\)。对于每个 \(i\)，只有跟 \(j\) 有关的是变量。于是我们将原式子变形
\[
-d[j]=a[i]\times b[j]+c[i]-f_i
\]

我们用线性规划来解决这个问题。用一次函数 \(y=kx+b\) 来描述这个方程。那么 \(y=-d[j],x=b[j]\)，并且 \(k=a[i],b=c[i]-f_i\)。我们现在需要 \(f_i\) 尽可能小，显然就是要 \(b=c[i]-f_i\) 尽可能大，也就是在 \(y\) 轴上的截距尽可能大。于是我们对于 \(1\sim i-1\) 间所有的 \(j\)，把 \((b[j],-d[j])\) 刻画在坐标轴上，再用 \(y=a[i]x+b\) 去做线性规划，如图。

显然需要截距最大时，直线必切于这些点的上凸包，于是我们只需要维护这一个上凸包即可。

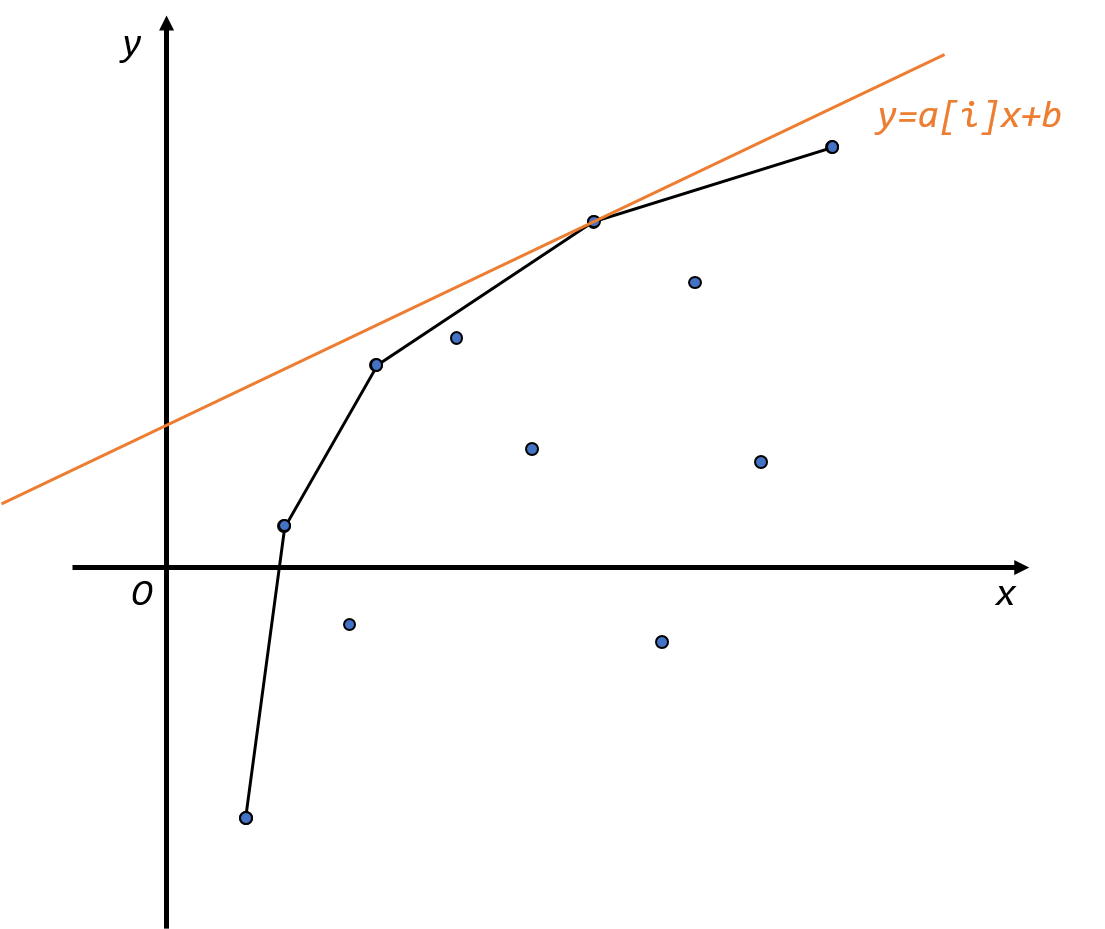
而如何在 \(i\) 不断枚举时，在不断有新的点加入的情况下去维护这一个上凸包呢？之前在提出问题的时候说明了，\(b[j]\) 是单调递增的，也就是说当我的循环变量 \(i\) 往右枚举时，新增的点会出现在所有之前的点的右边。我们开一个单调队列，单调队列中相邻的两点斜率是单调递减的。显然如果新加入的点会导致出现下图的情况，那么就把队尾的点删掉，因为它不可能再成为最优决策点。

而即使维护了这个上凸包，若还是用遍历凸包上的点来找最优决策点的话依旧是不可以的。于是这里需要决策单调性优化，之前也保证了 \(a[i]\) 是单调递减的，如图。那么显然若 \(i\) 的最优决策点为 \(j\)，那么 \(\forall i'\geq i\)，\(i'\) 的最优决策点 \(k\) 一定满足 \(k\geq j\)。

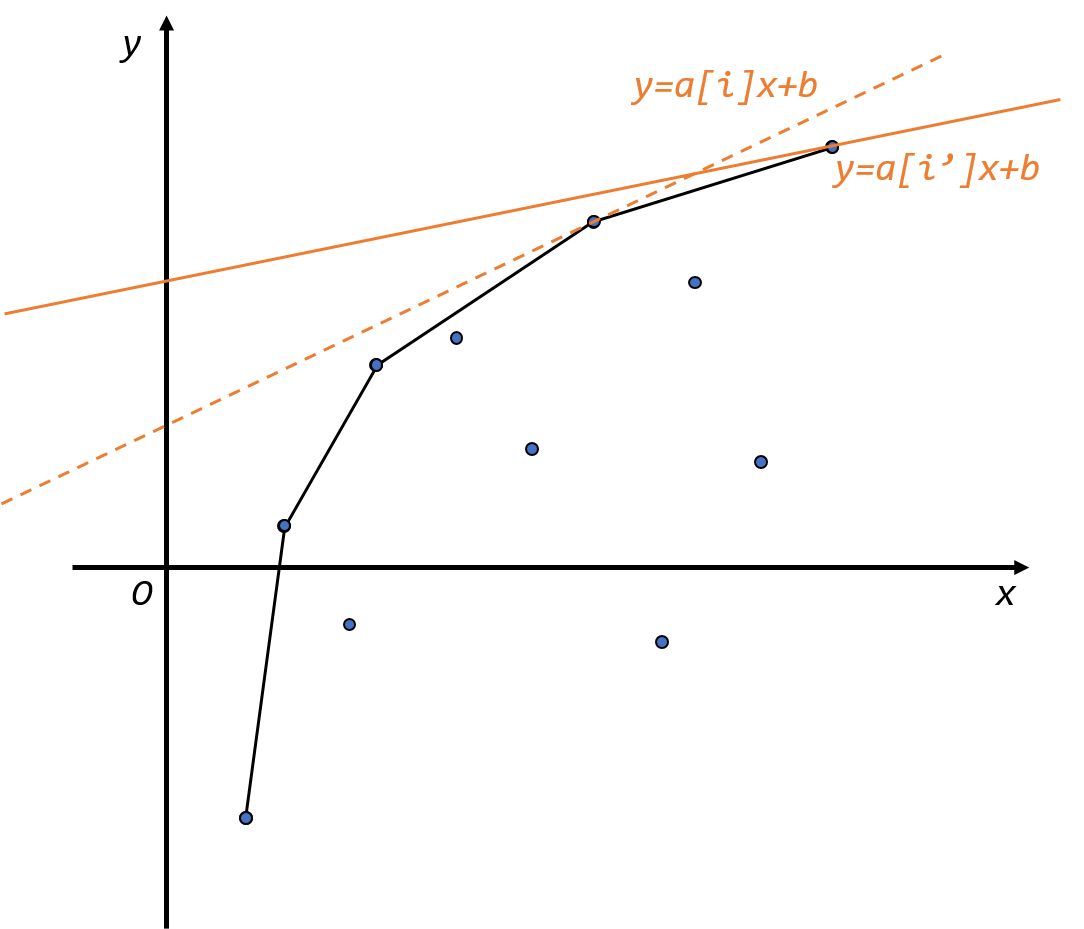
并且对于最优决策点，记它与之前的一个点斜率为 \(k_1\)，它与之后的一个点斜率为 \(k_2\)，是满足 \(k_1> a[i]> k_2\)。因此每当做决策前，我们先判断队首与次队首的斜率是否 \(>a[i]\)，若是，出队，直至队首与次队首的斜率 \(<a[i]\)。至此，队首元素就是对于 \(i\) 时的最优决策点。因此我们就可以 \(O(n)\) 解决这一问题了。

回到这一部分的最初的问题，究竟那些性质的 \(a,b\) 可以用决策单调性的斜率优化，并且原因又是什么呢？当然你可以通过画图来解释，但是下文将给出一个更加普适的原理。

决策单调性适用的原理——四边形不等式与决策单调性

在解释斜率优化那部分的遗留问题前，我们需要先对决策单调性这一整个部分进行归纳总结。

四边形不等式：对于任意 \(a\leq b\leq c\le d\)，有 \(w(a,d)+w(b,c)\geq w(a,c)+w(b,d)\)。

注意，四边形不等式不同于代数上的不等式。它只是一些 \(w\) 的二元函数具备的某种特殊性质。

定理：若 \(w(i,j)\) 满足四边形不等式，那么 1D/1D DP 是可以用决策单调性优化的。

实际上某些情况下不等号是 \(\leq\) 而不是 \(\geq\)。并且这两者适用的 DP 以及单调性是有些许差别的，具体地

• 当四边形不等式不等号取 \(\geq\) 时，若转移方程是取 \(\min\) 值，那么最优决策点与 \(i\) 的移动方向相同，并且单调；
• 当四边形不等式不等号取 \(\geq\) 时，若转移方程是取 \(\max\) 值，那么最优决策点与 \(i\) 的移动方向相反，并且单调；
• 当四边形不等式不等号取 \(\leq\) 时，若转移方程是取 \(\min\) 值，那么最优决策点与 \(i\) 的移动方向相反，并且单调；
• 当四边形不等式不等号取 \(\leq\) 时，若转移方程是取 \(\max\) 值，那么最优决策点与 \(i\) 的移动方向相同，并且单调。

注意，这四种不同的单调性差别值得注意，由于下文为了行文方便，均以第一种情况为例，千万不要以偏概全，对于题目要具体问题具体分析。

证明：以上述优化的第一种情形为例，即 \(f_i = \min\{f_j+w(i,j)\}\)，并且 \(w\) 要满足 \(w(a,d)+w(b,c)\geq w(a,c)+w(b,d)\)。
设 \(p_i\)​ 表示 \(i\) 的最优决策点是 \(p_i\)。那么有
\[f_{p_i}+w(p_i,i)\leq f_j+w(j,i)\tag{1}\]
同时，我们需要证明的式子是
\[f_{p_{i+1}}+w(p_{i+1},i+1)\leq f_j+w(j,i+1)\tag{2}\]
将 \((2)\) 式中 \(j\) 变为 \(p_i\)
\[f_{p_{i+1}}+w(p_{i+1},i+1)\leq f_{p_i}+w(p_i,i+1)\tag{3}\]
下面需要分情况讨论
1. \(p_{i+1}=i\)，那么显然 \(p_{i+1}=i\geq p_i\) 的，满足决策单调性；
2. \(p_{i+1}\neq i\)，将 \((1)\) 式中 \(j\) 变为 \(p_{i+1}\)，那么
\[f_{p_i}+w(p_i,i)\leq f_{p_{i+1}}+w(p_{i+1},i)\tag{4}\]
\((3)+(4)\) 得
\[w(p_{i+1},i+1)+w(p_i,i)\leq w(p_i,i+1)+w(p_{i+1},i)\]
因为 \(w\) 满足四边形不等式，因此 \(p_i\leq p_{i+1}\leq i\leq i+1\)。
综上满足 \(p_i\leq p_{i+1}\)，即满足决策单调性。
其余三种情况可以用同种方式证明，这里从简略去。读者可以自行证明。

既然如此，前文的单调队列优化以及斜率优化均利用到了决策单调性。那它们的 \(w\) 函数都是满足四边形不等式的，下面给出证明。为了方便下面默认四边形不等式是 \(\geq\) 的，并且 DP 值是取 \(\min\) 的。

对于单调队列优化来说，\(w(i,j)=a[i]+b[j]\)。那么对于 \(i\leq j\leq p\leq q\)
\[\begin{aligned}
w(i,q)+w(j,p)&=a[i]+b[q]+a[j]+b[p]\\
w(i,p)+w(j,q)&=a[i]+b[p]+a[j]+b[q]
\end{aligned}\]
由于 \(a[i]+b[q]+a[j]+b[p]=a[i]+b[p]+a[j]+b[q]\)。显然 \(w(i,q)+w(j,p)\geq w(i,p)+w(j,q)\)，满足四边形不等式。

对于斜率优化来说，\(w(i,j)=a[i]\times b[j]+c[i]+d[j]\)。那么对于 \(i\leq j\leq p\leq q\)
\[\begin{aligned}
w(i,q)+w(j,p)&=a[i]\times b[q]+c[i]+d[q]+a[j]\times b[p]+c[j]+d[p]\\
w(i,p)+w(j,q)&=a[i]\times b[p]+c[i]+d[p]+a[j]\times b[q]+c[j]+d[q]
\end{aligned}\]
要使其满足四边形不等式，即 \(a[i]\times b[q]+c[i]+d[q]+a[j]\times b[p]+c[j]+d[p]\geq a[i]\times b[p]+c[i]+d[p]+a[j]\times b[q]+c[j]+d[q]\)。等价于
\[a[i]\times b[q]+a[j]\times b[p]\geq a[i]\times b[p]+a[j]\times b[q]\]
那么至此，\(a,b\) 适用于决策单调性的斜率优化需满足的条件也迎刃而解了，即满足上式即可。

通过对 \(w\) 的符号的讨论，并且由排序不等式，对于上面的式子，更进一步的推论是，决策单调性的斜率优化需要满足的条件就是

• 当 \(w\) 符号取 \(\geq\)，DP 取 \(\min(\max)\) 值时，\(a\) 与 \(b\) 的单调性相反即可，只不过要根据决策点向左/向右移动来选择单调栈/单调队列维护。
• 当 \(w\) 符号取 \(\leq\)，DP 取 \(\min(\max)\) 值时，\(a\) 与 \(b\) 的单调性相同即可，同上。

其实本质上就是使得 \(w\) 有四边形不等式的性质。

因为内容编排的原因，至此给出决策单调性斜率优化的例题。

例题

• [APIO 2010]特别行动队
• [CEOI 2004]锯木厂选址
• [USACO 08MAR]土地购买
• [JSOI 2011]柠檬

\(w(i,j)\) 满足四边形不等式的更一般的情形——分治/二分数据结构

由上面的分析，我们可以得出对于 1D/1D 类 DP 的决策单调性优化是需要 \(w\) 满足四边形不等式的。不过之前举例的单调队列优化和斜率优化对于 \(w\) 的要求比较特殊，那么能不能有一种普适的做法使得让 \(w\) 只要满足四边形不等式就可以优化呢。

举例来说当 \(w(i,j)=\sqrt{j-i}\)，这个式子是满足 \(\forall a\leq b\leq c\leq d,w(a,d)+w(b,c)\leq w(a,c)+w(b,d)\)。不过式子中的 \(i,j\) 是不能像之前的情况一样独立出来的。于是我们考虑用别的方法来解决。

同样，为了行文方便，均以决策点向右移动为例。

分治

当 DP 方程满足
\[
f_i = \min(\max)\{g_j+w(i,j)\}
\]

其中 \(g\) 与 \(f\) 无关。这时，可以用分治的方法来解决。

例如，考虑我们需要得到 \([L,R]\) 这个区间的 DP 值，并且备选的决策区间是 \([l,r]\)。若对于 \(MID\left(MID=\frac{L+R}{2}\right)\) 这个位置的 DP 值取最优时的决策点是 \(loc\)，那么由决策单调性，\([L,MID-1]\) 的备选区间就是 \([l,loc]\)，而 \([MID+1,R]\) 的备选区间是 \([loc,r]\)。这样把问题分成两个子问题分治递归下去。

而如何找到 \(loc\)，方法是直接暴力扫 \([l,r]\) 中所有点作为决策点去转移到 \(MID\) 上，找到其中的最优值。以 CDQ 分治的思想，整个算法时间复杂度是 \(O(n\log n)\) 的。

由于转移时的 \(f\) 取值是不会受其他位置的 \(f\) 值的影响的，这样就保证了每个 \(f\) 的计算不需要先决条件，这样就能保证分治的正确性。

例题

• [POI 2011]Lightning Conductor
• [Codeforces 868F]Yet Another Minimization Problem

二分+数据结构

而当 DP 方程满足
\[
f_i = \min(\max)\{f_j+w(i,j)\}
\]

也就是说 \(f\) 的取值是受前面别的 \(f\) 的取值的影响的，这样分治的方法就不奏效了，这时有另外一个方法来解决——二分数据结构，通常使用二分+单调队列/单调栈来实现。

在方法讲解之前，我们需要给出一个引理。

引理：对于 \(w\) 满足四边形不等式的 DP 中 \(\forall i<j\)，如果在 \(i\) 处决策点 \(n\) 比 \(m\) 优秀（\(m<n\)），那么在 \(j\) 处 \(n\) 同样比 \(m\) 优秀。

证明：还是以 \(\geq\) 的四边形不等式以及取 \(\min\) 的 DP 方程为例。
由含义 \(m<n<i<j\)，那么满足四边不等式
\[w(m,j)+w(n,i)\geq w(m,i)+w(n,j)\tag{1}\]
又由于 \(n\) 在 \(i\) 点作为决策比 \(m\) 优，即
\[f_m+w(m,i)\geq f_n+w(n,i)\tag{2}\]
\((1)+(2)\) 得
\[f_m+w(m,j)\geq f_n+w(n,j)\]
得证。

在这之前我们所有的 DP 方法都是对于每个位置，考虑最优决策点。不过这个方法是对于每个位置，考虑其能成为哪些 DP 值的最优决策点。

由于满足决策单调性，显然最终每个位置的最优决策点是单调递增的，例如（数字表示每个位置的最优决策点，下标从 0 开始）
00112222234444666

在整个算法最开始时，由于考虑的决策点只有最初的 0，因此此时每个位置的最优决策都是 0，即
00000000000000000

对于 1 这个点由于只能从 0 这个点转移，因此 0 就是 1 的最优决策点，计算出 \(f_1\)。之后考虑 1 作为决策点对于哪些点来说能比 0 的决策更优。由之前引理，1 一定会是连续的一段后缀（也可能不存在），例如
00111111111111111

而如何找到最左端这个 1，我们可以二分来解决。对于二分的位置，如果它用 1 更新更优，那么把右端点左移，查找是否有更靠左的位置，否则左端点右移。找到最优点之后，那么右边这一段就全是 1 了。我们可以开一个三元组 \((i,l_i,r_i)\) 表示 \(i\) 这个决策点控制范围为 \([l_i,r_i]\) 用队列维护，这样就不用额外地赋值了。

以此类推，2 这个点从 1 转移，更新后续的决策点。循环把 \(1\sim n\) 做完即可。这其中，一共有三种不同的更新情形

1. 队尾区间未被完全覆盖，这个时候显然二分出最左端的更新位置之后，把当前队尾的右端点更新，再把新的这个三元组加进队尾。
2. 新的元素不比任何一个更优，我们只需要在二分前做一次特判，看新的元素更新 \(n\) 这个位置是否比之前的更优，若否，那么显然这个元素不可能成为后续的最优决策，舍掉。
3. 队尾区间能被完全覆盖，也就是说，例如原来的最优决策点是
   00112222234444666
   新加入的 7 这个点能完整地覆盖 6，如
   00112222234477777
   那么这时，我们只需在二分前把这种能被完全覆盖的区间去掉就可以了，操作方法是比较队尾元素作为决策点以及新的元素作为决策点转移到队尾元素控制的左端点哪一个更优，若新的元素能更优，把队尾弹出。重复操作后就可以按照 1. 的情形二分了。

几个要注意的小细节：

1. 二分的区间的左端点是经过第三种情形处理后的队尾元素的左端点，二分的右端点是 \(n\)。
2. 情形 3 是可以边二分边弹出队尾的。不过若这样做，一定要注意计算 DP 值的时候千万不要用后面的元素视作前面元素的决策。几个例子
   00112222234444666
   当你计算 4 这个区间的 DP 值时，千万不要拿 6 作为最优决策点来算，因为这样就不满足决策单调性了。所以还是建议先弹出不合法的队尾再进行二分。
3. 对于每个位置 \(i\)，它的最优决策点就是队首元素，不过如果队首元素控制范围的右端点在 \(i\) 前面，记得把这个队首弹出再取新的队首作为最优决策点。

同样，若决策点单调向左移动，可以用单调栈维护这个过程。

其实，适用于分治的 DP 式子也可以用这个方法做，不过这个方法同样也有一些缺陷，也就是单个 \(w\) 计算复杂度较高时，二分的复杂度会退化，也就起不到优化的目的了。

但是分治法中有一个暴力扫的过程，如果 \(w\) 可以通过上一个计算出的 \(w'\) 简易地推导出，那么分治法就可以解决这一类问题（当然前提还是 \(g\) 和 \(f\) 互不影响）。例如[Codeforces 868F]Yet Another Minimization Problem这题就只能分治法做。

例题

• [NOI 2009]诗人小G

小总结：

• \(f\) 与 \(g\) 无关，或者与此同时 \(w\) 不能简易计算出，选择分治法；
• \(w\) 能简易计算出，选择二分+数据结构的方法。

四边形不等式的一点补充

这里对四边形不等式做一些补充，以 \(\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)+w(b,c)\geq w(a,c)+w(b,d)\) 这样的四边形不等式为例。

我们取其中的一种特殊情况：取 \(i\leq i+1\leq j\leq j+1\)，那么 \(w(i,j+1)+w(i+1,j)\geq w(i,j)+w(i+1,j+1)\ (*)\)。

同时若 \(w\) 满足 \((*)\)，那么 \(w\) 也是满足四边形不等式的。即四边形不等式与 \((*)\) 式是等价条件。具体证明这里从略，感兴趣的读者可以自行证明。

另外，如果我们把 \((*)\) 式移项，得到 \(w(i+1,j)-w(i,j)\geq w(i+1,j+1)-w(i,j+1)\)。也就是说，随着决策点的右移 \(j+1\)，此时 \(w\) 的增长速率是小于 \(j\) 处的速率的。并且如果此时转移方程取 \(\min\)，显然如果某时 \(j+1\) 比 \(j\) 优秀，那么之后不可能会有 \(j\) 比 \(j+1\) 优秀。这样对应了之前总结的单调性规律，可以视为另一种证明。

四边形不等式的另一单调性优化

上文说到，如果对于 1D/1D DP，如果转移的代价函数 \(w\) 满足四边形不等式，如 \(\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)+w(b,c)\geq w(a,c)+w(b,d)\)，那么 \(f\) 的决策点是满足单调性的。除此之外，四边形不等式的一些性质在优化区间 DP 也有一定的作用。

问题引出：假设有区间 DP 的转移方程是 \(f_{l,r}=\min(\max)\{f_{l,k}+f_{k+1,r}+w(l,r)\}\)，如果 \(w\) 满足四边形不等式以及区间单调性，那么这个式子是可以利用某些单调性优化到 \(O(n^2)\) 的。

• 四边形不等式，还是以 \(\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)+w(b,c)\geq w(a,c)+w(b,d)\) 为例。
• 区间单调性，即 \(\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)\geq w(b,c)\)，即小区间的函数值不超过包含其的大区间。并且式中的不等号应时刻与四边形不等式的不等号方向一致。

对于不等号的方向和取 \(\min\) 还是取 \(\max\) 之间的关系，这里要说明的是当上述不等号取 \(\geq\) 时，对应的 DP 方程是要取 \(\min\) 的，并且单调性于枚举顺序相同。其余的可以参考上文决策单调性优化得出结论。下面还是以这一种为例。

先不加证明地引出两个引理。（不证明是考虑到引理证出来意义不大，并且没有必要。如果你感兴趣可以参考《动态规划加速原理之四边形不等式(赵爽)》这篇文章）

引理一 对于 DP 方程，\(f_{l,r}=\min\{f_{l,k}+f_{k+1,r}+w(l,r)\}\)，若 \(w\) 满足四边形不等式和区间单调性，那么 DP 函数 \(f\) 同样满足四边形不等式。

引理二 设 \(s_{l,r}\) 是 \(f_{l,r}\) 的最优决策点。如果 \(f\) 满足四边形不等式，那么会有 \(s_{i,j}\leq s_{i,j+1}\leq s_{i+1,j+1}\)。

四边形不等式定理 若利用引理二的单调性，即 \(s_{i,j-1}\leq s_{i,j}\leq s_{i+1,j}\)，来优化该区间 DP，其复杂度是可以降低至 \(O(n^2)\) 的。

证明：从区间 DP 的本质入手，我们考虑当区间长度为 \(\delta\) 时枚举的量。对于每个左端点：
\(l=1\)，\((l,l+\delta-1)\) 枚举长度是 \(s_{l+1,l+\delta-1}-s_{l,l+\delta-2}=s_{2,\delta}-s_{1,\delta-1}\)；
\(l=2\)，枚举长度是 \(s_{3,1+\delta}-s_{2,\delta}\)；
\(l=3\)，枚举长度是 \(s_{4,2+\delta}-s_{3,1+\delta}\)；
\(\vdots\)
\(l=n+1-\delta\)，枚举长度是 \(s_{n+2-\delta,n}-s_{n+1-\delta,n-1}\)。
把上式相加，总长度是 \(s_{n+2-\delta,n}-s_{1,\delta-1}\leq n\)。又由于总共有 \(n\) 个不同的 \(\delta\)，因此总复杂度为 \(O(n^2)\)。

事实上，更多的方程并不是长 \(f_{l,r}=\min(\max)\{f_{l,k}+f_{k+1,r}+w(l,r)\}\) 这个样子，更多的会是 \(f_{i,j}=\min(\max)\{f_{k,j-1}+w(k+1,i)\}\)。大致意思是前 \(i\) 元素分为 \(j\) 个区间得到的最小/大价值。这里值得补充的是如果 \(w\) 满足四边形不等式，可以证明 \(f\) 同样满足四边形不等式，同样可以优化。

容易发现，这个方程和前文所述 1D/1D 类 DP 决策单调性优化是一样的，因此这些 DP 会有多种优化方式。不过不同的方式优化还是有些许复杂度上的差异，请读者自行思考。

例题

• [IOI 2000]邮局

不满足决策单调性的斜率优化

咕

带权二分优化（DP 凸优化）

咕

数据结构优化

咕

参考文献

• FlashHu，博客园，『DP的各种优化（动态规划，决策单调性，斜率优化，带权二分，单调栈，单调队列）』
• grannychan，博客园，『「算法总结」DP常用优化』
• ww3113306，洛谷题解，『题解 - [NOI2009]诗人小G』
• XDU_Skyline，CSDN，『动态规划专题小结：四边形不等式优化』
• 罗勇军，CSDN，『算法竞赛专题解析（10）：DP优化(1)--四边形不等式』