NOIp2018集训test-9-17(am)

这是一套去年在长沙考过的题，但是我当时就没理清楚＋没写题解(我以前很多博客都写得跟shi一样，完全没有意义，看到就想打当时的我)，所以又考得稀烂。

T1.star way to heaven

容易想到二分＋并查集，二分距离所有星星和边界的最小距离r，也就是距离这些点r以内的范围不能走，也就是看以每个点为圆心r为半径的圆能不能把上下都堵满。

这个做法会被卡成80分。正解是用最小生成树代替二分的过程。答案一定是两个点间的距离，最小生成树相当于是从小到大的枚举答案，可以满足当连接一条边权为w的边时，距离小于w的点都联通了，最后答案就是从上边界走到下边界的树上路径上的最大边权（去掉这条边就能不连通啦）。我写成了整颗树上的最大边权然后爆0了。

 //Achen
 #include<bits/stdc++.h>
 #define For(i,a,b) for(int i=(a);i<=(b);i++)
 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
 #define Formylove return 0
 const int N=;
 using namespace std;
 typedef long long LL;
 typedef double db;
 int n,m,k;
 db ans;

 template<typename T>void read(T &x) {
     char ch=getchar(); T f=; x=;
     while(ch!='-'&&(ch<''||ch>'')) ch=getchar();
     if(ch=='-') f=-,ch=getchar();
     for(;ch>=''&&ch<='';ch=getchar()) x=x*+ch-''; x*=f;
 }

 struct node {
     int x,y;
 }p[N];

 LL pf(LL x) { return x*x; }

 LL get_dis(int a,int b) {
     if(a>b) swap(a,b);
     if(a<=n&&b<=n) return pf(p[a].x-p[b].x)+pf(p[a].y-p[b].y);
     else if(a<=n&&b==n+) return pf(m-p[a].y);
     else if(a<=n&&b==n+) return pf(p[a].y);
     else if(a==n+&&b==n+) pf(m);
 }

 int ecnt,fir[N],nxt[N<<],to[N<<];
 LL val[N<<];
 void add(int u,int v,LL w) {
     nxt[++ecnt]=fir[u]; fir[u]=ecnt; to[ecnt]=v; val[ecnt]=w;
     nxt[++ecnt]=fir[v]; fir[v]=ecnt; to[ecnt]=u; val[ecnt]=w;
 }

 LL dfs(int x,int fa,LL mx) {
     if(x==n+) return mx;
     for(int i=fir[x];i;i=nxt[i]) if(to[i]!=fa) {
         LL tp=dfs(to[i],x,max(mx,val[i]));
         if(tp!=) return tp;
     }
     return ;
 } 

 LL dis[N];
 int pr[N];
 int vis[N];
 void prim() {
     memset(dis,/,sizeof(dis));
     dis[n+]=;
     For(i,,n+) {
         int kk=;
         For(j,,n+) if(!vis[j]) {
             if(!kk||dis[j]<dis[kk]) kk=j;
         }
         add(pr[kk],kk,dis[kk]);
         dis[kk]=;
         vis[kk]=;
         For(j,,n+) if(!vis[j]) {
             LL d=get_dis(j,kk);
             if(dis[kk]+d<dis[j]) {
                 pr[j]=kk;
                 dis[j]=dis[kk]+d;
             }
         }
     }
 }

 #define ANS
 int main() {
 #ifdef ANS
     freopen("starway.in","r",stdin);
     freopen("starway.out","w",stdout);
 #endif
     read(n); read(m); read(k);
     n=k;
     For(i,,k) {
         read(p[i].x);
         read(p[i].y);
     }
     prim();
     ans=dfs(n+,,);
     ans=sqrt(ans)/2.0;
     printf("%.8lf\n",ans);
     Formylove;
 }

T2.God knows

这题好神啊。当年我在长沙看了一天才看懂（大概只是当时以为懂？）， 然后现在根本不知道我当时在想/写些啥子。。

一句话题解就是，线段树维护单调栈优化dp。

把p[i]看成高度，删除一个点就是删掉所有它前面比它高的和它后面比他矮的，那么删除的一定是一个高度单增的序列，且满足不在序列里的数一定存在它前面高度比它高或者它后面高度比它矮的数在序列中，也就是说这是一个极长上升序列。f[i]表示选以i结尾的极长上升序列的答案，f[i]就是通过i之前的一个高度小于i的j，且j是j~i中比i矮的中最高的一个，这样的j来更新i,这样的j所在的是一个由i之前的比i矮的数组成的单调降的单调队列。

考虑如何维护这个单调队列？保证在i之前只要按i从小到大扫就好，要比i矮可以用线段树维护（一开始是标号从小到大对应高度从大到小的单调队列，现在线段树上高度从小到大，那么对应的就是一个标号从大到小的单调队列），那么现在只要在线段树一个区间内维护单降队列就ok了。

线段树如何维护单调队列，参考楼房重建一题。还是解释一下代码以免以后看来想打自己，按高度建线段树，线段树上每个节点维护s[x],sl[x]两个pr，s[x]表示以当前区间做单调队列，(队列中的最大值，队列中的数的最小f值)，sl[x]表示当前区间的左子区间在合并右子区间（合并后左边队列会在队尾上弹一些元素对吧）后的s的情况，用一个函数calc(l,r,x)表示l,r的区间做单调队列，最后入队的元素是x时队列的情况，这样就可以做了，具体参考代码。

 //Achen
 #include<bits/stdc++.h>
 #define For(i,a,b) for(int i=(a);i<=(b);i++)
 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
 #define Formylove return 0
 #define inf 0x7777777
 const int N=2e5+;
 using namespace std;
 typedef long long LL;
 typedef double db;
 int n,p[N],c[N],f[N];

 template<typename T>void read(T &x) {
     char ch=getchar(); T f=; x=;
     while(ch!='-'&&(ch<''||ch>'')) ch=getchar();
     if(ch=='-') f=-,ch=getchar();
     for(;ch>=''&&ch<='';ch=getchar()) x=x*+ch-''; x*=f;
 }

 #define pr pair<int,int>
 #define fi first
 #define se second
 #define lc (x<<1)
 #define rc ((x<<1)|1)
 #define mid ((l+r)>>1)
 #define mp make_pair
 pr s[N<<],sl[N<<];

 pr operator +(const pr&A,const pr&B) {
     if(A.fi==) return B; if(B.fi==) return A;
     return mp(max(A.fi,B.fi),min(A.se,B.se));
 }

 void build(int x,int l,int r) {
     s[x]=sl[x]=mp(,inf); //A1
     if(l==r) return;
     build(lc,l,mid); build(rc,mid+,r);
 }

 pr calc(int x,int l,int r,int last) {
     if(l==r) { return s[x].fi>last?s[x]:mp(,inf); }
     if(s[rc].fi>last) return sl[x]+calc(rc,mid+,r,last);
     else return calc(lc,l,mid,last);
 }

 void upd(int x,int l,int r) {
     s[x]=s[lc]+s[rc];
     sl[x]=calc(lc,l,mid,s[rc].fi);
 }

 void update(int x,int l,int r,int pos,pr t) {
     if(l==r) { s[x]=t; return ; }
     if(pos<=mid) update(lc,l,mid,pos,t);
     else update(rc,mid+,r,pos,t);
     upd(x,l,r);
 }

 pr rs; //(0,inf)
 void qry(int x,int l,int r,int ql,int qr) {
     if(l>=ql&&r<=qr) { rs=rs+calc(x,l,r,rs.fi); return; }
     if(qr>mid) qry(rc,mid+,r,ql,qr);
     if(ql<=mid) qry(lc,l,mid,ql,qr);
 }

 #define ANS
 int main() {
 #ifdef ANS
     freopen("knows.in","r",stdin);
     freopen("knows.out","w",stdout);
 #endif
     read(n);
     For(i,,n) read(p[i]);
     For(i,,n) read(c[i]);
     build(,,n);
     For(i,,n) {
         rs=mp(,inf);
         qry(,,n,,p[i]);
         f[i]=rs.fi==?c[i]:rs.se+c[i];
         update(,,n,p[i],mp(i,f[i]));
     }
     rs=mp(,inf);
     qry(,,n,,n);
     printf("%d\n",rs.se);
     Formylove;
 }
 /*
 5
 3 1 4 5 2
 3 4 3 4 1
 */

T3.Lost my music

代码十分短小优美，用大佬的写题解方式就是：这是一道可持久化栈维护凸包的裸题。

我记得这题是可持久化栈维护凸包，但是并打不来。

题目要求的是一个斜率形式，画到图上就是求前面的点到我的斜率的最小值，

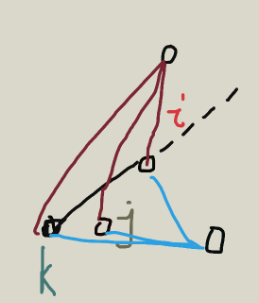如图，中间的j点无论如何都不优，所以维护的这样一个上凸壳

并且我和我在凸壳上的前一个点的斜率就是我的答案（我考场上竟然写了在凸包上三分，我到底在想些什么？？？)

凸壳是用单调栈维护的，这个在树上就得搞个可持久化栈了。可持久化栈用倍增实现，f[x][i]表示凸壳上我前面的2^i个点，弹栈的时候就可以倍增地弹，就相当于回溯到那个点所维护的凸壳的状态。

Rep(i,18,0) if(f[tx][i]&&f[f[tx][i]][0]&&dcmp(xl(f[tx][i],x)-xl(f[tx][i],f[f[tx][i]][0])>=0)) {
		tx=f[f[tx][i]][0];
}
if(f[tx][0]&&dcmp(xl(tx,x)-xl(tx,f[tx][0])>=0)) tx=f[tx][0];

因为我弹的时候是从我前面的前面开始弹的，相当于没考虑只弹一个的情况，所以要有下面那句等于特判。

 //Achen
 #include<bits/stdc++.h>
 #define For(i,a,b) for(int i=(a);i<=(b);i++)
 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
 #define Formylove return 0
 const int N=5e5+;
 using namespace std;
 typedef long long LL;
 typedef double db;
 int n,c[N],f[N][];
 db ans[N];

 template<typename T>void read(T &x) {
     char ch=getchar(); T f=; x=;
     while(ch!='-'&&(ch<''||ch>'')) ch=getchar();
     if(ch=='-') f=-,ch=getchar();
     for(;ch>=''&&ch<='';ch=getchar()) x=x*+ch-''; x*=f;
 }

 int ecnt,fir[N],nxt[N<<],to[N<<];
 void add(int u,int v) {
     nxt[++ecnt]=fir[u]; fir[u]=ecnt; to[ecnt]=v;
 }

 int d[N];
 #define eps 1e-10
 int dcmp(db x) { return fabs(x)<eps?:(x>?:-); }
 db xl(int a,int b) {
     return (-c[a]+c[b])/((db)d[a]-d[b]);
 }

 void DFS(int x,int p) {
     d[x]=d[p]+;
     int tx=p;
     Rep(i,,) if(f[tx][i]&&f[f[tx][i]][]&&dcmp(xl(f[tx][i],x)-xl(f[tx][i],f[f[tx][i]][])>=)) {
         tx=f[f[tx][i]][];
     }
     if(f[tx][]&&dcmp(xl(tx,x)-xl(tx,f[tx][])>=)) tx=f[tx][];
     f[x][]=tx;
     if(x!=) ans[x]=xl(tx,x);
     For(i,,) f[x][i]=f[f[x][i-]][i-];
     for(int i=fir[x];i;i=nxt[i])
         DFS(to[i],x);
 }

 #define ANS
 int main() {
 #ifdef ANS
     freopen("lost.in","r",stdin);
     freopen("lost.out","w",stdout);
 #endif
     read(n);
     For(i,,n) read(c[i]);
     For(i,,n) {
         int fx;
         read(fx);
         add(fx,i);
     }
     DFS(,);
     For(i,,n) printf("%.10lf\n",ans[i]);
     Formylove;
 }