poj-1511

从1节点到所有节点的最短路和，加上所有节点返回1节点的最短路和，刚开始的方法时间复杂度有毒啊

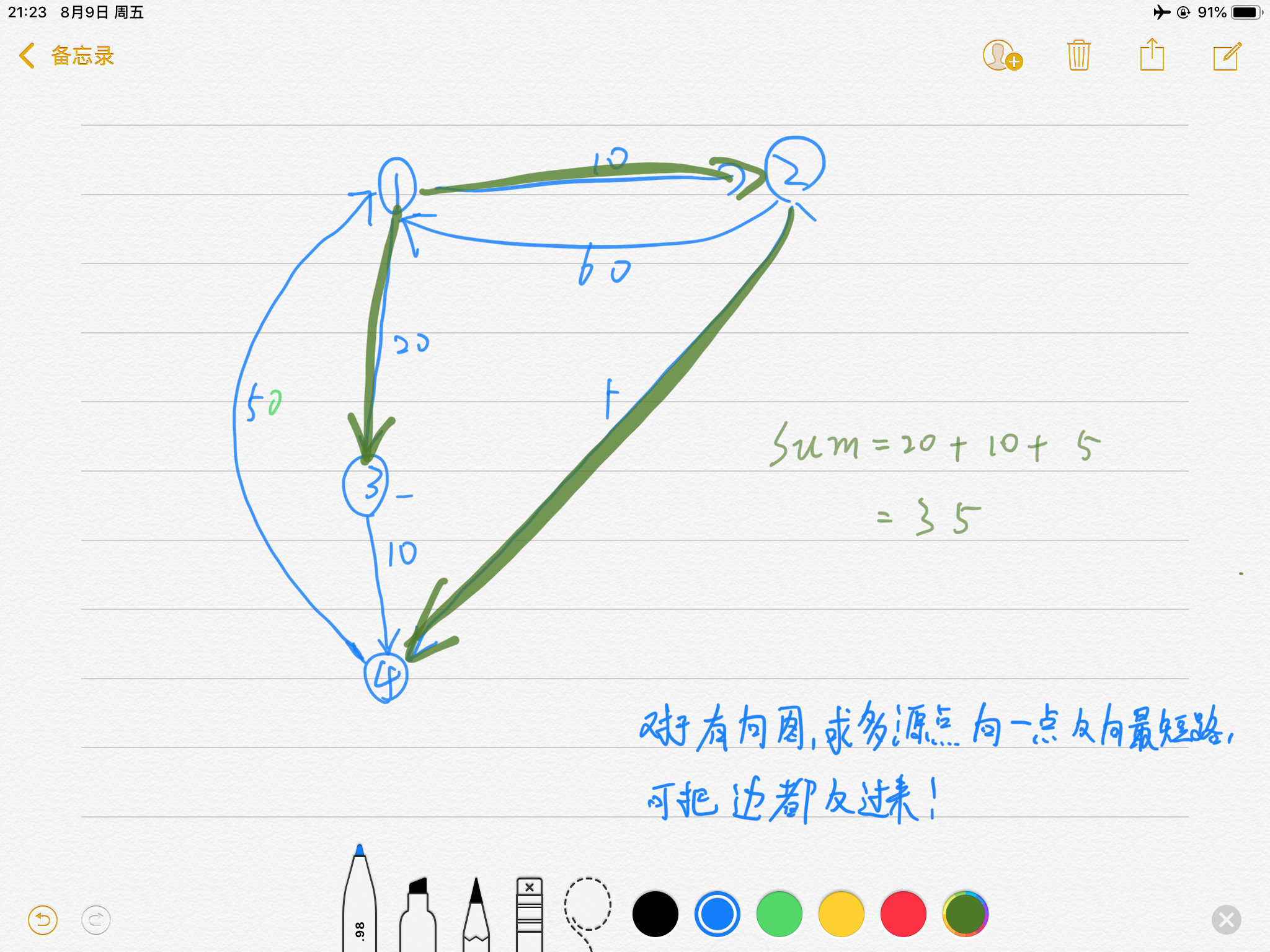
其实只要把边全反向重装一次就好了哈哈哈

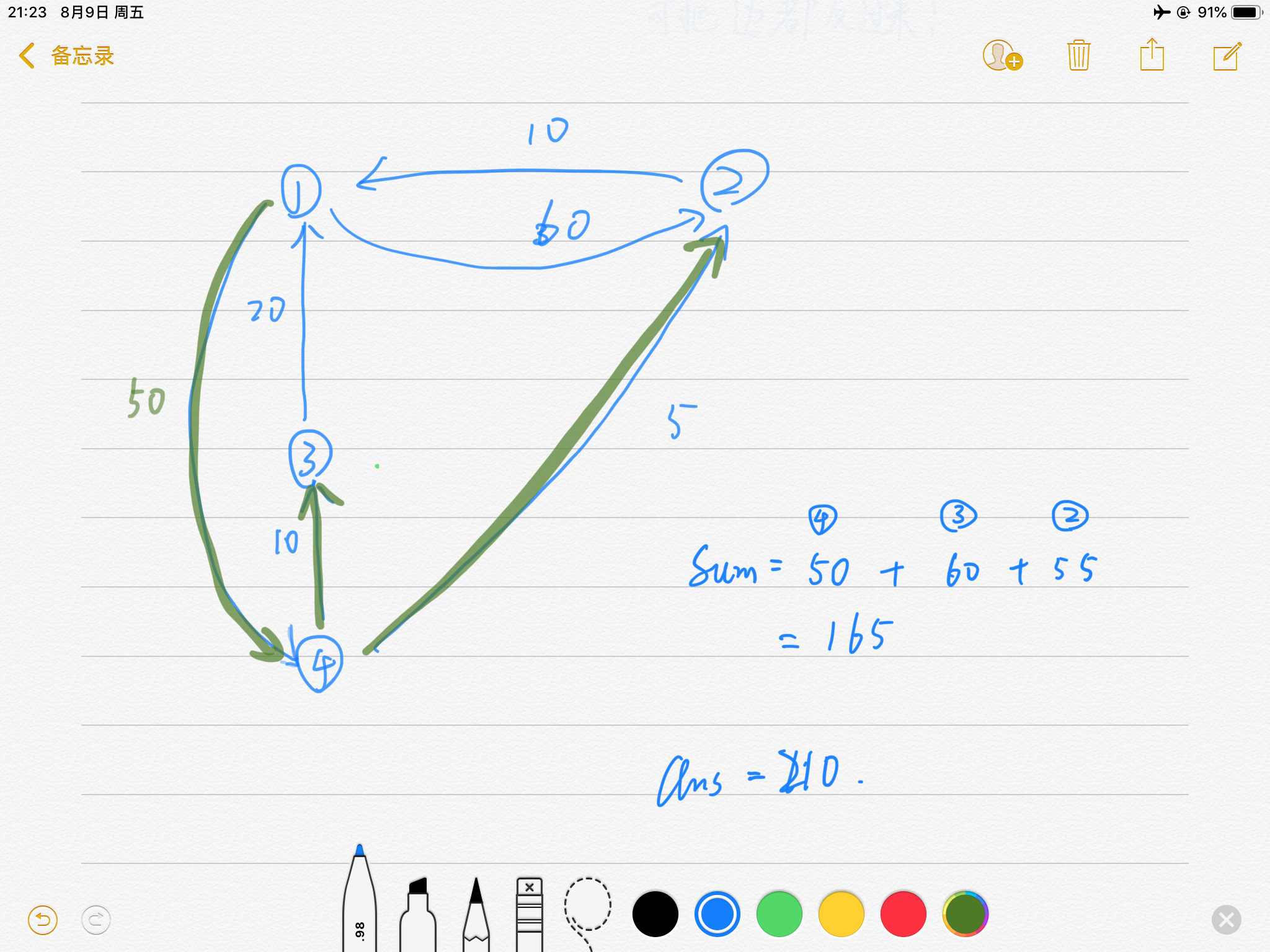
好了就是这样，套路了一个dijkstra+优先队列

#include<cstdio>
#include<queue>
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 1000000 + 100;
typedef long long ll;
int n, m;
int dis[maxn];
int vis[maxn];
int head[maxn];

struct Node {
	int to;
	int len;
	int next;
}G[maxn];

bool operator < (const Node a, const Node b) {
	if (a.len > b.len) return true;
	else return false;
}
int cnt = 1;

void insert(int be, int en, int len) {
	G[cnt].to = en; G[cnt].next = head[be]; head[be] = cnt; G[cnt].len = len;//头插法
	cnt++;
}

int dijstra(int be) {
	memset(vis, 0, sizeof(vis));
	for (int i = 0; i <= n; i++) dis[i] = INF;
	dis[be] = 0;
	priority_queue<Node>que;
	Node a;
	a.to = be;
	a.len = 0;
	que.push(a);
	while (!que.empty()) {
		Node ans = que.top();
		que.pop();
		if (vis[ans.to] == 0) {
			vis[ans.to] = 1;
			for (int i = head[ans.to]; i; i = G[i].next) {
				int p = G[i].to;
				if (!vis[p] && dis[p] > dis[ans.to] + G[i].len) {
					dis[p] = dis[ans.to] + G[i].len;
					Node ac;
					ac.len = dis[p];
					ac.to = p;
					que.push(ac);
				}
			}
		}
	}
	return 0;
}
int T;
int list_be[maxn];
int list_en[maxn];
int list_val[maxn];
int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d %d", &n, &m);
		memset(head, 0, sizeof(head));
		cnt = 1;
		int a, b, c;
		for (int i = 0; i < m; i++) {
			scanf("%d %d %d", &a, &b, &c);
			list_be[i] = a;
			list_en[i] = b;
			list_val[i] = c;
			insert(a, b, c);
		}
		dijstra(1);
		ll ans = 0;
		for (int i = 1; i <= n; i++) {
			ans += dis[i];
		}
		memset(head, 0, sizeof(head));
		cnt = 1;
		for (int i = 0; i < m; i++) {
			insert(list_en[i], list_be[i], list_val[i]);
		}
		dijstra(1);
		for (int i = 1; i <= n; i++) {
			ans += dis[i];
		}
		printf("%lld\n", ans);
	}
	return 0;
}