@总结 - 1@ 多项式乘法 —

@0 - 参考资料@
@1 - 一些概念@
@2 - 傅里叶正变换@
@3 - 傅里叶逆变换@
@4 - 迭代实现 FFT@
@5 - 参考代码实现@
@6 - 快速数论变换 NTT@
@7 - 任意模数 NTT@
- @三模数 NTT@
- @拆系数 fft (mtt)@
@8 - 例题与应用@

@0 - 参考资料@

@1 - 一些概念@

多项式的系数表示法：形如 $A(x)=a_0+a_1x+...+a_{n-1}x^{n-1}$。

多项式的点值表示法：对于 n-1 次多项式 $A(x)$，我们选取 n 个不同的值 $x_0, x_1, ... , x_{n-1}$ 代入 $A(x)$，得到 $y_i=A(x_i)$。则 $(x_0, y_0),...,(x_{n-1},y_{n-1})$ 称为多项式的点值表示。

把多项式系数当作 n 个变量，n 个点当作 n 个线性方程，可以用高斯消元求得唯一解。因此，我们可以用这 n 个点唯一表示 A(x) 。

注意，一个多项式的点值表示法并不是唯一的。

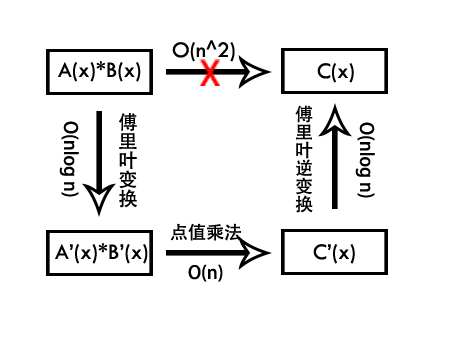
如果用点值表示法的多项式作乘法，可以直接把纵坐标相乘，在 O(n) 的时间实现多项式乘法。

FFT（快速傅里叶变换）可以实现 O(nlog n) 的点值表示与系数表示之间的转换。

一个解释多项式乘法原理的图：

复数：复数简单来说就是 $a + bi$，其中$i^2=-1$。可以发现复数 $a + bi$ 与二维平面上的向量 $(a, b)$ 一一对应。

复数的乘法可以直接(a + bi)(c + di)展开相乘。但是几何上复数乘法还有另一种解释：

这样定义下，复数的乘法为模长相乘，幅角相加。

单位根：定义 n 次单位根为使得 $z^n=1$ 成立的复数 $z$。一共 n 个，在单位圆上且 n 等分单位圆。

可以发现 n 次单位根模长都为 1，幅角依次为$0*\frac{2\pi}{n},1*\frac{2\pi}{n},...,(n-1)*\frac{2\pi}{n}$。

我们记 n 次单位根依次为$w_n^0,w_n^1,...w_n^{n-1}$。

有以下几个性质：

（1）$w_{n}^{i}*w_{n}^{j}=w_{n}^{i+j}$

（2）$w_{dn}^{dk}=w_n^k$，有点类似于分数的约分。

（3）$w_{2n}^k=-w_{2n}^{k+n}$。

以上几个性质都可以从幅角的方面去理解。

@2 - 傅里叶正变换@

FFT 的正变换实现，是基于对多项式进行奇偶项分开递归再合并的分治进行的。

对于 n-1 次多项式，我们选择插入 n 次单位根求出其点值表达式。

记多项式$A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}$。

再记$A_o(x)=a_1+a_3x+a_5x^2+...$。

再记$A_e(x)=a_0+a_2x+a_4x^2+...$。

有$A(x)=x*A_o(x^2)+A_e(x^2)$。

令 $n = 2*p$。则有：

$A(w_n^k)=w_n^k*A_o[(w_{n/2}^{k/2})^2]+A_e[(w_{n/2}^{k/2})^2]=w_n^k*A_o(w_p^k)+A_e(w_p^k)$；

$A(w_n^{k+p})=w_n^{k+p}*A_o(w_p^{k+p})+A_e(w_p^{k+p})=-w_n^k*A_o(w_p^k)+A_e(w_p^k)$

在已知 $A_o(w_p^k)$ 与 $A_e(w_p^k)$ 的前提下，可以 O(1) 算出 $A(w_n^k)$ 与 $A(w_n^{k+p})$。

因此，假如我们递归求解 $A_o(x),A_e(x)$ 两个多项式 p 次单位根的插值，就可以在O(n)的时间内算出 $A(x)$ n 次单位根的插值。

时间复杂度是经典的 $T(n)=2*T(n/2)+O(n)=O(n\log n)$。

@3 - 傅里叶逆变换@

观察我们刚刚的插值过程，实际上就是进行了如下的矩阵乘法。

$\begin{bmatrix} (w_n^0)^0 & (w_n^0)^1 & \cdots & (w_n^0)^{n-1} \\ (w_n^1)^0 & (w_n^1)^1 & \cdots & (w_n^1)^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (w_n^{n-1})^0 & (w_n^{n-1})^1 & \cdots & (w_n^{n-1})^{n-1} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \begin{bmatrix} A(w_n^0) \\ A(w_n^1) \\ \vdots \\ A(w_n^{n-1}) \end{bmatrix}$

我们记上面的系数矩阵为 $V$。

对于下面定义的 $D$：

$D = \begin{bmatrix} (w_n^{-0})^0 & (w_n^{-0})^1 & \cdots & (w_n^{-0})^{n-1} \\ (w_n^{-1})^0 & (w_n^{-1})^1 & \cdots & (w_n^{-1})^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (w_n^{-(n-1)})^0 & (w_n^{-(n-1)})^1 & \cdots & (w_n^{-(n-1)})^{n-1} \end{bmatrix}$

考虑 $D*V$的结果：

$(D*V)_{ij}=\sum_{k=0}^{k<n}d_{ik}*v_{kj}=\sum_{k=0}^{k<n}w_n^{-ik}*w_{n}^{kj}=\sum_{k=0}^{k<n}w_n^{k(j-i)}$

当 i = j 时，$(D*V)_{ij}=n$；

当 i ≠ j 时，$(D*V)_{ij}=1+w_n^{j-i}+(w_n^{j-i})^2+...=\frac{1-(w_n^{j-i})^n}{1-w_n^{j-i}}$=0；

【根据定义，n 次单位根的 n 次方都等于 1】

所以：$\frac1n*D=V^{-1}$

因此将这个结果代入最上面那个公式里面，有：

$\begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \frac1n \begin{bmatrix} (w_n^{-0})^0 & (w_n^{-0})^1 & \cdots & (w_n^{-0})^{n-1} \\ (w_n^{-1})^0 & (w_n^{-1})^1 & \cdots & (w_n^{-1})^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (w_n^{-(n-1)})^0 & (w_n^{-(n-1)})^1 & \cdots & (w_n^{-(n-1)})^{n-1} \end{bmatrix}\begin{bmatrix} A(w_n^0) \\ A(w_n^1) \\ \vdots \\ A(w_n^{n-1}) \end{bmatrix}$

“这样，逆变换就相当于把正变换过程中的 $w_n^k$ 换成 $w_n^{-k}$，之后结果除以 n 就可以了。”——摘自某博客。

……

还是有点难理解。比如为什么我们不直接把$w_n^k$ 换成 $\frac1n*w_n^{-k}$ 算了。

实际上，因为$w_n^{-k}=w_n^{n-k}$，也就是说它 TM 还是一个 n 次单位根。所以我们插值还是正常的该怎么插怎么插。如果换成 $\frac1n*w_n^{-k}$ 它就不是一个单位根，以上性质就不满足了。

@4 - 迭代实现 FFT@

递归版本的 FFT 虽好，可奈何常数太大。

我们考虑怎么迭代实现 FFT。观察奇偶分组后各数的位置。

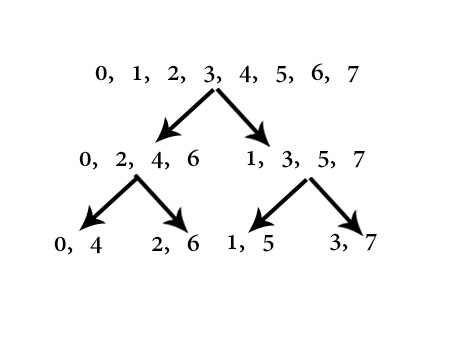
原序列：0,1,2,3,4,5,6,7。

终序列：0,4,2,6,1,5,3,7。

转换为二进制再来看看。

原序列：000,001,010,011,100,101,110,111。

终序列：000,100,010,110,001,101,011,111。

可以发现终序列是原序列每个元素的翻转。

于是我们可以先把要变换的系数排在相邻位置，从下往上迭代。

这个二进制翻转过程可以自己脑补方法，只要保证时间复杂度O(nlog n)，代码简洁就可以了。

在这里给出一个参考的方法：

我们对于每个 i，假设已知 i-1 的翻转为 j。考虑不进行翻转的二进制加法怎么进行：从最低位开始，找到第一个为 0 的二进制位，将它之前的 1 变为 0，将它自己变为 1。因此我们可以从 j 的最高位开始，倒过来进行这个过程。

@5 - 参考代码实现@

本代码为 uoj#34 的AC代码。在代码中有些细节可以关注一下。

#include<cmath>

#include<cstdio>

#include<algorithm>

using namespace std;

const int MAXN = 400000;

const double PI = acos(-1);

struct complex{

	double r, i;

	complex(double _r=0, double _i=0):r(_r), i(_i){}

};//C++ 有自带的复数模板库，但很显然我并不会。

typedef complex cplx;

cplx operator +(cplx a, cplx b){return cplx(a.r+b.r, a.i+b.i);}

cplx operator -(cplx a, cplx b){return cplx(a.r-b.r, a.i-b.i);}

cplx operator *(cplx a, cplx b){return cplx(a.r*b.r-a.i*b.i, a.r*b.i+b.r*a.i);}

void FFT(cplx *A, int n, int type) {

	for(int i=0,j=0;i<n;i++) {

		if( i < j ) swap(A[i], A[j]);

		for(int k=(n>>1);(j^=k)<k;k>>=1);//这个地方读不懂就背吧。。。

	}

	for(int s=2;s<=n;s<<=1) {

		int t = (s>>1);

		cplx u = cplx(cos(type*PI/t), sin(type*PI/t));

//这个地方需要注意一点：如果题目中需要反复用到 FFT，则可以预处理出所有单位根以减小常数。

		for(int i=0;i<n;i+=s) {

			cplx r = cplx(1, 0);

			for(int j=0;j<t;j++,r=r*u) {

				cplx e = A[i+j], o = A[i+j+t];

				A[i+j] = e + r*o; A[i+j+t] = e - r*o;

			}

		}

	}

}

cplx A[MAXN + 5], B[MAXN + 5], C[MAXN + 5];

int main() {

	int n, m;

	scanf("%d%d", &n, &m); n++, m++;

	for(int i=0;i<n;i++)

		scanf("%lf", &A[i].r);

	for(int i=0;i<m;i++)

		scanf("%lf", &B[i].r);

	int len = 1;

	while( len < (n+m-1) ) len <<= 1;

//此处重点：由于我们每一次都要奇偶分组，所以长度必须为2的整数次幂，高位补0就好了。

//还有一点：A 与 B 的乘积最高次数为 n+m-1，而不是 n 也不是 m。

	FFT(A, len, 1); FFT(B, len, 1);

	for(int i=0;i<len;i++)

		C[i] = A[i] * B[i];

	FFT(C, len, -1);

	for(int i=0;i<n+m-1;i++)

		printf("%d ", int(round(C[i].r/len)));//记得，一定要记得除以len。

}

@6 - 快速数论变换 NTT@

实际上这可以算是 FFT 的一个优化。

FFT虽然跑得快，但是因为是浮点数运算，终究还是有精度、常数等问题。

然而问题来了：我们多项式乘法都是整数在那里搞来搞去，为什么一定要扯到浮点数。是否存在一个在模意义下的，只使用整数的方法？

想一想我们用了哪些单位根的性质：

（1）$w_{n}^{i}*w_{n}^{j}=w_{n}^{i+j}$

（2）$w_{dn}^{dk}=w_n^k$

（3）$w_{2n}^k=-w_{2n}^{k+n}$

（4） n 个单位根互不相同，且 $w_n^0=1$

我们能否找到一个数，在模意义下也满足这些性质？

引入原根的概念：对于素数 p，p 的原根 G 定义为使得 $G^0,G^1,...,G^{p−2}(\mod p)$ 互不相同的数。

再定义 $g_n^k = (G^{\frac{p-1}{n}})^k$。验证一下这个东西是否满足单位根的以上性质。

（1），由幂的运算立即可得。

（2），由幂的运算立即可得。

（3），$g_{2n}^{k+n}=(G^{\frac{p-1}{2n}})^{k+n}=(G^{\frac{p-1}{2n}})^k*(G^{\frac{p-1}{2n}})^n=G^{\frac{p-1}{2}}*g_{2n}^k=-g_{2n}^k(\mod p)$。

【因为$G^{p-1}=1(\mod p)$且由原根定义$G^{\frac{p-1}{2}}\not=G^{p-1}(\mod p)$，故$G^{\frac{p-1}{2}}=-1(\mod p)$】

（4），由原根的定义立即可得。

所以我们就可以搞 NTT 了。直接把代码中涉及单位根的换成原根即可。

然而，可以发现 NTT 适用的模数 m 十分有限。它应该满足以下性质：

（1）令 $m = 2^p*k+1$，k 为奇数，则多项式长度必须 $n \le 2^p$。

（2）方便记忆，方便记忆，与方便记忆。（其实我后来发现记不住可以直接现场暴力求。。。）

这里有一些合适的模数【来源：miskcoo】。

NTT 参考代码，一样是 uoj 的那道题。

#include<cstdio>

#include<algorithm>

using namespace std;

const int MOD = 998244353;

const int MAXN = 400000;

const int G = 3;

int pow_mod(int b, int p) {

	int ret = 1;

	while( p ) {

		if( p & 1 ) ret = 1LL*ret*b%MOD;

		b = 1LL*b*b%MOD;

		p >>= 1;

	}

	return ret;

}

void NTT(int *A, int n, int type) {

	for(int i=0,j=0;i<n;i++) {

		if( i > j ) swap(A[i], A[j]);

		for(int l=(n>>1);(j^=l)<l;l>>=1);

	}

	for(int s=2;s<=n;s<<=1) {

		int t = (s>>1), u = (type == 1) ? pow_mod(G, (MOD-1)/s) : pow_mod(G, (MOD-1)-(MOD-1)/s);

		for(int i=0;i<n;i+=s) {

			for(int j=0,p=1;j<t;j++,p=1LL*p*u%MOD) {

				int e = A[i+j], o = 1LL*A[i+j+t]*p%MOD;

				A[i+j] = (e + o)%MOD, A[i+j+t] = (e + MOD - o)%MOD;

			}

		}

	}

}

int A[MAXN + 5], B[MAXN + 5], C[MAXN + 5];

int main() {

	int n, m;

	scanf("%d%d", &n, &m); n++, m++;

	for(int i=0;i<n;i++)

		scanf("%d", &A[i]);

	for(int i=0;i<m;i++)

		scanf("%d", &B[i]);

	int len = 1; while( len < n+m-1 ) len <<= 1;

	NTT(A, len, 1); NTT(B, len, 1);

	for(int i=0;i<len;i++)

		C[i] = 1LL*A[i]*B[i]%MOD;

	NTT(C, len, -1);

	int inv = pow_mod(len, MOD-2);

	for(int i=0;i<n+m-1;i++)

		printf("%d ", 1LL*C[i]*inv%MOD);

}

@7 - 任意模数 NTT@

假如题目中规定了模数怎么办？还卡 FFT 的精度怎么办？

有两种方法：

@三模数 NTT@

我们可以选取三个适用于 NTT 的模数 M1，M2，M3 进行 NTT，用中国剩余定理合并得到 x mod (M1*M2*M3) 的值。只要保证 x < M1*M2*M3 就可以直接输出这个值。

之所以是三模数，因为用三个大小在 10^9 左右模数对于大部分题目来说就足够了。

但是 M1*M2*M3 可能非常大怎么办呢？难不成我还要写高精度？其实也可以。

我们列出同余方程组：

\[\begin{cases}
x \equiv a_1&\mod m_1\\
x \equiv a_2&\mod m_2\\
x \equiv a_3&\mod m_3\\
\end{cases}\]

先中国剩余定理（这个不会……我真的帮不了 qwq）合并前两个方程组：

\[\begin{cases}
x \equiv A&\mod M\\
x \equiv a_3&\mod m_3\\
\end{cases}
\]

其中 M = m1*m2 < 10^18。

然后将第一个方程变形得到 $x = kM + A$ 代入第二个方程：

\[kM+A \equiv a_3\mod m_3\\
k \equiv (a_3-A)*M^{-1} \mod m_3\\
\]

令 $Q = (a_3-A)*M^{-1} $，则 $k = Pm_3 + Q$。

再将上式代入回 $x = kM + A$，得 $x = (Pm_3 + Q)M+ A = Pm_3M+QM+A$。

又因为 $M = m_1m_2$，所以 $x = Pm_1m_2m_3 + QM + A$。

也就是说 $x \equiv QM + A \mod m_1m_2m_3$。

然后……然后就这样啊。

一份 luoguP4243 的 AC 代码：

#include<cstdio>

#include<algorithm>

using namespace std;

typedef long long ll;

const ll G = 3;

const int MAXN = 400000;

const ll MOD[3] = {469762049, 998244353, 1004535809};

//模数记不住怎么办？身为一名 OIer 啊，就要做自己最擅长的事情（指暴力打表）。

ll pow_mod(ll b, ll p, ll mod) {

	ll ret = 1;

	while( p ) {

		if( p & 1 ) ret = ret*b%mod;

		b = b*b%mod;

		p >>= 1;

	}

	return ret;

}

ll mul_mod(ll a, ll b, ll mod) {

	ll ret = 0;

	while( a ) {

		if( a & 1 ) ret = (ret + b)%mod;

		b = (b + b)%mod;

		a >>= 1;

	}

	return ret;

}

ll inv[3][3], M, k1, k2, Inv;

void init() {

	for(int i=0;i<3;i++)

		for(int j=0;j<3;j++)

			if( i != j ) inv[i][j] = pow_mod(MOD[i], MOD[j]-2, MOD[j]);

	M = MOD[0]*MOD[1];

	k1 = mul_mod(MOD[1], inv[1][0], M);

	k2 = mul_mod(MOD[0], inv[0][1], M);

	Inv = inv[0][2]*inv[1][2]%MOD[2];

}

ll CRT(ll a1, ll a2, ll a3, ll mod) {

	ll A = (mul_mod(a1, k1, M) + mul_mod(a2, k2, M))%M;

	ll K = (a3 + MOD[2] - A%MOD[2])%MOD[2]*Inv%MOD[2];

	return ((M%mod)*K%mod + A)%mod;

}

//27 ~ 40 行，三模数 NTT 的精华 owo

ll f[3][MAXN + 5], g[3][MAXN + 5];

void ntt(ll *A, int n, int m, int type) {

	for(int i=0, j=0;i<n;i++) {

		if( i < j ) swap(A[i], A[j]);

		for(int l=(n>>1);(j^=l)<l;l>>=1);

	}

	for(int s=2;s<=n;s<<=1) {

		int t = (s>>1);

		ll u = (type == -1) ? pow_mod(G, (MOD[m]-1)/s, MOD[m]) : pow_mod(G, (MOD[m]-1) - (MOD[m]-1)/s, MOD[m]);

		for(int i=0;i<n;i+=s) {

			ll p = 1;

			for(int j=0;j<t;j++,p=p*u%MOD[m]) {

				ll x = A[i+j], y = A[i+j+t]*p%MOD[m];

				A[i+j] = (x + y)%MOD[m], A[i+j+t] = (x + MOD[m] - y)%MOD[m];

			}

		}

	}

	if( type == -1 ) {

		ll inv = pow_mod(n, MOD[m]-2, MOD[m]);

		for(int i=0;i<n;i++)

			A[i] = A[i]*inv%MOD[m];

	}

}

ll h[3][MAXN + 5];

int main() {

	int n, m; ll p; init();

	scanf("%d%d%lld", &n, &m, &p); n++, m++;

	for(int i=0;i<n;i++) {

		scanf("%lld", &f[2][i]);

		f[1][i] = f[2][i] % MOD[1];

		f[0][i] = f[2][i] % MOD[0];

	}

	for(int i=0;i<m;i++) {

		scanf("%lld", &g[2][i]);

		g[1][i] = g[2][i] % MOD[1];

		g[0][i] = g[2][i] % MOD[0];

	}

	int len; for(len = 1;len < n+m-1;len <<= 1);

	for(int i=0;i<3;i++) {

		ntt(f[i], len, i, 1); ntt(g[i], len, i, 1);

		for(int j=0;j<len;j++)

			h[i][j] = f[i][j]*g[i][j]%MOD[i];

		ntt(h[i], len, i, -1);

	}

	for(int i=0;i<n+m-1;i++)

		printf("%lld ", CRT(h[0][i], h[1][i], h[2][i], p));

}

@拆系数 fft (mtt)@

对于题目所给定的模数 M，我们求出其平方根 $S = \lfloor\sqrt{M}\rfloor$。如果 M 在 10^9 范围内，则 S 在 3*10^4 左右。

然后我们将需要进行 fft 的系数 ai 拆成 $a_i = \lfloor\frac{a_i}{S}\rfloor*S + (a_i\mod S) = b_i*S + c_i$ 的形式。

于是将两个多项式 A1, A2 作卷积可以转化为 B1, C1 与 B2, C2 之间分别作卷积，再通过上面的式子合并起来。

因为 B 和 C 的系数值域都在 3*10^4 的范围以内，所以 double 产生的误差不大会影响结果（看运气，建议还是用 long double）。

这样一共需要 7 次 fft（比上面那个三模数要少 2 次）

上面是拆系数 fft 的基本思路，但我们还可以进行进一步地优化。

这个优化的起始点在于观察到 fft 时我们只传了实数进去，而 fft 时我们运用的是复数进行运算，这样直观上就会产生一些“浪费”。

利用复数的虚数部分，我们可以将两个实系数多项式通过一次 fft 进行插值。

具体而言，假如我们要插值的是 n 项的多项式 A 和 B。

令 P = A + B*i, Q = A - B*i。再令 A'[k], B'[k], P'[k], Q'[k] 表示插值后第 k 位上的数。

然后我们开始推式子（其中 conj 是复数的共轭）：

\[Q'[k]
= \sum_{p=0}^{n-1}(a_p - b_p*i)*\omega_{n}^{k*p} \\
= \sum_{p=0}^{n-1}(a_p - b_p*i)*conj(\omega_{n}^{(n-k)*p}) (由单位根的性质)\\
= \sum_{p=0}^{n-1}conj(a_p + b_p*i)*conj(\omega_{n}^{(n-k)*p})\\
= \sum_{p=0}^{n-1}conj((a_p + b_p*i)*\omega_{n}^{(n-k)*p})\\
= conj(P'[n-k])
\]

又因为 A'[k] = (P + Q)/2, B'[k] = (P - Q)/(2*i) = i*(Q - P)/2，所以就实现了我们最初的目的。

由此可以将 7 次 fft 降为 5 次。

可以将还原的过程也两个合成一个，但是因为插完值过后的系数变为了复数，所以上述结论不再适用。

不过有更为简单的结论：令 R'[k] = A'[k] + B'[k]*i，则 R = A + B*i（但我好像不会证。。。打表试验搞出来的）（update in 2020/02/12：这个显然的。。。。）。

这样 5 次又少一次，变为了 4 次。

可以发现这是一个足够优秀的算法，因为我们的 ntt 至少也需要 3 次插值。

一样是 luoguP4243 的 AC 代码：

（double 误差过不了.jpg）

#include<cstdio>

#include<cmath>

#include<algorithm>

using namespace std;

const int MAXN = 100000;

const long double PI = acos(-1);

typedef long long ll;

struct complex{

    long double r, i;

    complex(long double _r=0, long double _i=0):r(_r), i(_i){};

    friend complex conj(complex x) {

        return complex(x.r, -x.i);

    }

    friend complex operator +(complex x, complex y) {

        return complex(x.r + y.r, x.i + y.i);

    }

    friend complex operator -(complex x, complex y) {

        return complex(x.r - y.r, x.i - y.i);

    }

    friend complex operator *(complex x, complex y) {

        return complex(x.r*y.r - x.i*y.i, x.r*y.i + y.r*x.i);

    }

    friend complex operator /(complex x, long double k) {

        return complex(x.r/k, x.i/k);

    }

};

void fft(complex *A, int n, int type) {

    for(int i=0,j=0;i<n;i++) {

        if( i < j ) swap(A[i], A[j]);

        for(int k=(n>>1);(j^=k)<k;k>>=1);

    }

    for(int s=2;s<=n;s<<=1) {

        int t = (s>>1);

        complex u = complex(cos(PI/t), sin(type*PI/t));

        for(int i=0;i<n;i+=s) {

            complex p = complex(1, 0);

            for(int j=0;j<t;j++,p=p*u) {

                complex x = A[i+j], y = p*A[i+j+t];

                A[i+j] = (x + y), A[i+j+t] = (x - y);

            }

        }

    }

    if( type == -1 ) {

        for(int i=0;i<n;i++)

            A[i] = A[i] / n;

    }

}

int length(int x) {

    int len; for(len = 1; len < x; len <<= 1);

    return len;

}

complex a1[4*MAXN + 5], a2[4*MAXN + 5];

complex b1[4*MAXN + 5], b2[4*MAXN + 5];

complex Q[4*MAXN + 5], P[4*MAXN + 5];

int main() {

    int n, m, p; scanf("%d%d%d", &n, &m, &p), n++, m++;

    int len = length(n + m - 1), sq = sqrt(p);

    for(int i=0;i<n;i++) {

        int x; scanf("%d", &x), x %= p;

        P[i] = complex(x/sq, x%sq);

    }

    for(int i=0;i<m;i++) {

        int x; scanf("%d", &x), x %= p;

        Q[i] = complex(x/sq, x%sq);

    }

    fft(P, len, 1), fft(Q, len, 1);

    for(int i=0;i<len;i++) {

        a1[i] = (conj(P[(len-i)%len]) + P[i])/2;

        a2[i] = (conj(P[(len-i)%len]) - P[i])/2*complex(0, 1);

        b1[i] = (conj(Q[(len-i)%len]) + Q[i])/2;

        b2[i] = (conj(Q[(len-i)%len]) - Q[i])/2*complex(0, 1);

    }

    for(int i=0;i<len;i++) {

    	P[i] = a1[i]*b2[i] + a2[i]*b1[i];

        Q[i] = a1[i]*b1[i] + complex(0, 1)*a2[i]*b2[i];

    }

    fft(Q, len, -1), fft(P, len, -1);

    for(int i=0;i<len;i++)

        if( i < n + m - 1 )

            printf("%lld ", (ll(Q[i].r+0.5)%p*sq%p*sq%p + ll(P[i].r+0.5)%p*sq%p + ll(Q[i].i+0.5)%p)%p);

}

@8 - 例题与应用@

@分治 FFT@

算是 FFT 的一个简单的扩展吧。。。

其问题大致可以描述为：

$C$ 是 $A,B$ 的卷积，其中 $B$ 是一开始就已知的。依次给出 $a_0, a_1,\dots$ 的值，当给出 $a_i$ 的值时，需要立即算出 $c_i$ 的值。

解决方法就是使用 cdq 分治 + FFT。如果你不知道 cdq 分治是什么也没关系，只需要知道它是个分治就 OK。

假如我们已知 $[le, mid]$ 内所有的 $A[i]$，则 $[le, mid]$ 对 $[mid+1, ri]$ 的贡献为：

\[C[i] += \sum_{le \le j\le mid}^{j+k=i}A[j]*B[k]（mid+1 \le i \le ri）
\]

可以求出 k 的范围为 1 <= k <= ri-le。这是一个长度为 ri - le 的卷积，可以用 FFT 来优化。

我们递归时先递归左边，再卷积计算左边那一半对右边那一半的贡献，最后递归右边。

注意分治的区间长度不一定要是 2 的幂。

@例题@ ： @codeforces - 553E@ Kyoya and Train

我写的题解（可能比较冗长……）

@多维卷积@

对于含有多个变量的多项式，比如 $f(x, y) = a_{00}x^0y^0 + a_{01}x^0y^1 + ...+ a_{0m}x^0y^m + a_{10}x^1y^1 + ... + a_{nm}x^ny^m$。

考虑怎么快速将它们相乘。

我们一样转为点值形式，通过代入单位根的二元组 $(w_n^i, w_m^j)$（即令 $x = w_n^i, y = w_m^j$ 得到的多项式的值）求出共 n * m 个点值，再对应位置相乘。

可以理解为将第一维相同的项放在一起，对第二维进行代入单位根；再将第二维相同的项放在一起，对第一位进行代入单位根。

逆变换同理。

也可以把 $x^iy^j$ 看成 $z^{i*(2*m+1)+j}$ 转为一维卷积来做。

一般运用在二维矩阵中的卷积问题，或是将二进制看成多维卷积 + 循环卷积来做。

@例题@ ： @codechef - BUYLAND@ Buying Land。

这里有一份题解

这种卷积题居然在 5, 6 年前就有人研究了……真可怕。

@循环卷积@

有一类特殊的卷积长这样：

\[c_{(i+j)\mod n} = \sum_{0\le i<n,0\le j<n}a_i*b_j
\]

我们将这类卷积称为循环卷积。

一般而言，循环卷积有两种解决方案。

一是使用正常的卷积，再把大于等于 n 的部分加到前面去。

二是将循环卷积转为点值表示，逐位相乘，再逆变换回去。

但是这个时候我们不能随便把卷积的长度变长变短，必须让它保持长度为 n。

注意到如果 $x^n = 1$ 则 $x^{n+i} = x^i$，相当于指数取模。这个取模和循环卷积的取模非常的相似。

因此，可以通过代入 n 次单位根将循环卷积转换为点值表示。但是如果 n 不是 2 的幂就无法使用分治解决了。

因为无法使用分治，这个方法是 $O(n^2)$。但是在多次乘法的时候它具有一定的优越性，比如矩阵快速幂。

第二种方案，说明循环卷积与正常卷积具有一定的统一性，或者说正常卷积本就是循环卷积的一种特例。

@例题@ ： @codechef - BIKE@ Chef and Bike，是 2017 冬令营的题。

这里有一份题解

从入门到进阶再到出门已经安排得明明白白了。