Problem B. Harvest of Apples（杭电2018年多校+组合数+逆元+莫队）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6333

题目：

题意：求C(n,0)+C(n,1)+……+C(n,m)的值。

思路：由于t和n数值范围太大，所以此题查询复杂度不能太高，由组合数的将前k项求和可以推出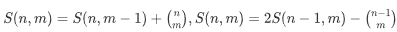，从而可以转换成莫队的区间查询，将n当成l，m当成r即可。此题需要注意，对于求组合数得用o(1)的方法求，也就是阶乘相除的方法，对于分母我们得求逆元，因而借助欧拉定理。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef pair<ll, ll> pll;
 typedef pair<ll, int> pli;
 typedef pair<int, ll> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long ull;

 #define lson i<<1
 #define rson i<<1|1
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = 1e9 + ;
 const int maxn = 1e5 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f;

 int t, block;
 ll sum;
 ll a[maxn], b[maxn];

 struct node {
     int l, r, id;
     ll ans;
     bool operator < (const node & x) const {
         return (l - ) / block == (x.l - ) / block ? r < x.r : l < x.l;
     }
 }ask[maxn];

 ll Mod_Pow(ll x, ll n) {
     ll res = ;
     while(n > ) {
         if(n & ) res = res * x % mod;
         x = x * x % mod;
         n >>= ;
     }
     return res;
 }

 void init() {
     a[] = ;
     for(int i = ; i < maxn; i++) a[i] = a[i-] * i % mod;
     for(int i = ; i < maxn; i++) b[i] = Mod_Pow(a[i], mod - );
 }

 ll C(int n, int m) {
     if(n <  || m <  || m > n) return ;
     if(m ==  || m == n) return ;
     return a[n] * b[n-m] % mod * b[m] % mod;
 }

 int main() {
     //FIN;
     init();
     scanf("%d", &t);
     block = sqrt(maxn);
     sum = ;
     for(int i = ; i <= t; i++) {
         scanf("%d%d", &ask[i].l, &ask[i].r);
         ask[i].id = i;
     }
     sort(ask + , ask + t + );
     for(int i = , l = , r = ; i <= t; i++) {
         while(l < ask[i].l) sum = ( * sum - C(l++, r) + mod) % mod;
         while(l > ask[i].l) sum = ((sum + C(--l, r)) * b[]) % mod;
         while(r < ask[i].r) sum = (sum + C(l, ++r)) % mod;
         while(r > ask[i].r) sum = (sum - C(l, r--) + mod) % mod;
         ask[ask[i].id].ans = sum;
     }
     for(int i = ; i <= t; i++) {
         printf("%lld\n", ask[i].ans);
     }
     return ;
 }