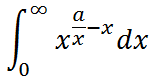洛谷4525 & 4526:【模板】自适应辛普森法——题解
参考:https://phqghume.github.io/2018/05/19/%E8%87%AA%E9%80%82%E5%BA%94%E8%BE%9B%E6%99%AE%E6%A3%AE%E6%B3%95/ 以及洛谷不多的题解。
辛普森推导过程就看参考吧,当然你要想看懂推导需要:
1.会高中导数那点东西,至少知道原函数怎么求。
2.粗略了解定积分。
3.知道微积分第一、第二基本定理(从知乎上找的:https://www.zhihu.com/question/21439225)。
然后推导就很简单了,实际上就是用的是将任意曲线近似转换成二次函数曲线去求。
————————————————————
https://www.luogu.org/problemnew/show/P4525
计算积分
结果保留至小数点后6位。
数据保证计算过程中分母不为0且积分能够收敛。
这就是自适应辛普森的板题了,eps开到1e-12大概就能过了。
(话说为什么要“自适应”?那当然是因为精度的原因啦,我们左右分一下将答案求和和一个区间的答案比较一下没有多少误差就return就行啦。)
#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double dl;
const dl eps=1e-;
dl a,b,c,d,L,R;
inline dl f(dl x){
return (c*x+d)/(a*x+b);
}
inline dl simpson(dl l,dl r){
dl mid=(l+r)/;
return (f(l)+*f(mid)+f(r))*(r-l)/;
}
inline dl asr(dl l,dl r,dl ans){
dl mid=(l+r)/;
dl l1=simpson(l,mid),r1=simpson(mid,r);
if(fabs(l1+r1-ans)<eps)return l1+r1;
return asr(l,mid,l1)+asr(mid,r,r1);
}
int main(){
scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&L,&R);
printf("%lf\n",asr(L,R,simpson(L,R)));
return ;
}
————————————————————
https://www.luogu.org/problemnew/show/P4526
计算积分
保留至小数点后5位。若积分发散,请输出"orz"。
挺吓人的,但思考a<0显然就发散了。
a>=0时a越大收敛得越慢,于是打表,大概得出来x=12时就已经约为0了。
于是L=eps,R=12跑一遍自适应辛普森法即可。
#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double dl;
const dl eps=1e-;
dl a;
inline dl f(dl x){
return pow(x,a/x-x);
}
inline dl simpson(dl l,dl r){
dl mid=(l+r)/;
return (f(l)+*f(mid)+f(r))*(r-l)/;
}
inline dl asr(dl l,dl r,dl ans){
dl mid=(l+r)/;
dl l1=simpson(l,mid),r1=simpson(mid,r);
if(fabs(l1+r1-ans)<eps)return l1+r1;
return asr(l,mid,l1)+asr(mid,r,r1);
}
int main(){
scanf("%lf",&a);
if(a<)puts("orz");
else printf("%.5lf\n",asr(eps,,simpson(eps,)));
return ;
}
+++++++++++++++++++++++++++++++++++++++++++
+本文作者:luyouqi233。 +
+欢迎访问我的博客:http://www.cnblogs.com/luyouqi233/+
+++++++++++++++++++++++++++++++++++++++++++
洛谷4525 & 4526:【模板】自适应辛普森法——题解的更多相关文章
- 洛谷 P4525 & P4526 [模板] 自适应辛普森积分
题目:https://www.luogu.org/problemnew/show/P4525 https://www.luogu.org/problemnew/show/P4526 学习辛普森积分:h ...
- 洛谷P3387 【模板】缩点 题解
背景 今天\(loj\)挂了,于是就有了闲情雅致来刷\(luogu\) 题面 洛谷P3387 [模板]缩点传送门 题意 给定一个\(n\)个点\(m\)条边有向图,每个点有一个权值,求一条路径,使路径 ...
- 洛谷.4525.[模板]自适应辛普森法1(Simpson积分)
题目链接 Simpson积分公式:\[\int_a^bf(x)dx\approx\frac{b-a}{6}\left[f(a)+f(b)+4f(\frac{a+b}{2})\right]\] 推导过程 ...
- 洛谷 P3385 【模板】负环 题解
P3385 [模板]负环 题目描述 暴力枚举/SPFA/Bellman-ford/奇怪的贪心/超神搜索 寻找一个从顶点1所能到达的负环,负环定义为:一个边权之和为负的环. 输入格式 第一行一个正整数T ...
- 洛谷P4526 【模板】自适应辛普森法2
P4526 [模板]自适应辛普森法2 洛谷传送门 题目描述 计算积分 保留至小数点后5位.若积分发散,请输出"orz". 输入格式 一行,包含一个实数,为a的值 输出格式 一行,积 ...
- 洛谷P4525 【模板】自适应辛普森法1与2
洛谷P4525 [模板]自适应辛普森法1 与P4526[模板]自适应辛普森法2 P4525洛谷传送门 P4525题目描述 计算积分 结果保留至小数点后6位. 数据保证计算过程中分母不为0且积分能够收敛 ...
- P4526 【模板】自适应辛普森法2
P4526 [模板]自适应辛普森法2 #include <bits/stdc++.h> using namespace std; ; double a; inline double f(d ...
- P4525 【模板】自适应辛普森法1
P4525 [模板]自适应辛普森法1 #include <bits/stdc++.h> using namespace std; ; double a, b, c, d, l, r; in ...
- FFT/NTT总结+洛谷P3803 【模板】多项式乘法(FFT)(FFT/NTT)
前言 众所周知,这两个东西都是用来算多项式乘法的. 对于这种常人思维难以理解的东西,就少些理解,多背板子吧! 因此只总结一下思路和代码,什么概念和推式子就靠巨佬们吧 推荐自为风月马前卒巨佬的概念和定理 ...
随机推荐
- WeTest功能优化第3期:业内首创,有声音的云真机
第3期功能优化目录 [云真机远程调试]音频同步传输实现测试有声 [兼容性测试报告]新增视频助力动态定位问题 [云真机远程调试]菜单栏优化助力机型选择 本期介绍的新功能,秉承创造用户需求的理念,在云真机 ...
- python学习笔记03 --------------程序交互与格式化输出
1.读取用户输入内容 语法:input() 例: name = input('你的名字是?) print('你好'+name) 程序会等待用户输入名字后打印:你好(用户输入的名字) 注意:input接 ...
- 关于@media不生效的问题和meta总结
1:之前做的是两套页面.现在改成响应式布局.发现加上 @media only screen and (max-width: 500px) { .gridmenu { width:1 ...
- 【转】MMO即时战斗:技能实现
转自 http://blog.csdn.net/cyblueboy83/article/details/41628743 一.前言 基本所有MMO游戏无论是回合制.策略类.即时战斗等等类型都需要有相应 ...
- Skype for Business Server 方案
方案说明: 高可用性的配置屏蔽了单点故障,使得当一个服务器节点失效时,另外的可用的节点能够进行服务的接管.可伸缩性的配置可以保证当即时沟通平台的使用用户增加时,该平台应该具有良好的可伸缩性,能非常方便 ...
- 饥饿的小易(枚举+广度优先遍历(BFS))
题目描述 小易总是感觉饥饿,所以作为章鱼的小易经常出去寻找贝壳吃.最开始小易在一个初始位置x_0.对于小易所处的当前位置x,他只能通过神秘的力量移动到 4 * x + 3或者8 * x + 7.因为使 ...
- 图像质量评价指标之 PSNR 和 SSIM
1. PSNR (Peak Signal-to-Noise Ratio) 峰值信噪比 给定一个大小为 \(m×n\) 的干净图像 \(I\) 和噪声图像 \(K\),均方误差 \((MSE)\) 定义 ...
- [转载]Tensorflow中reduction_indices 的用法
Tensorflow中reduction_indices 的用法 默认时None 压缩成一维
- Python3 Tkinter-Scrollbar
1.创建 from tkinter import * root=Tk() Scrollbar(root).pack() root.mainloop() 2.设置silder的位置 from tkint ...
- C Program进阶-二维数组动态内存开辟
对于二维数组,我们知道可以用Type ArrayName[Row][Colume]的方式来定义,这是一种静态内存开辟的方式,程序在编译的时候就为该数组分配了空间,而且行和列大小也是指定的.这篇文章里我 ...