BZOJ3223：文艺平衡树——超详细题解

http://www.lydsy.com/JudgeOnline/problem.php?id=3223

题面复制于洛谷。

题目背景

这是一道经典的Splay模板题——文艺平衡树。

题目描述

您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作：翻转一个区间，例如原有序序列是5 4 3 2 1，翻转区间是[2,4]的话，结果是5 2 3 4 1

输入输出格式

输入格式：

第一行为n,m n表示初始序列有n个数，这个序列依次是(1,2, \cdots n-1,n)(1,2,⋯n−1,n) m表示翻转操作次数

接下来m行每行两个数 [l,r][l,r] 数据保证 1 \leq l \leq r \leq n1≤l≤r≤n

输出格式：

输出一行n个数字，表示原始序列经过m次变换后的结果

输入输出样例

输入样例#1：

5 3
1 3
1 3
1 4

输出样例#1：

4 3 2 1 5

说明

N,M<=100000

——————————————————————————————————

这里就要用到splay翻转区间的操作了。

我们首先考虑，假设我们翻转整个区间的话，那十分的好办——以根节点为对称轴将其他点全都“对称”过去即可。

比如原图如下

我们变成

这显然是正确的。

该操作可以简述为：交换当前结点的左右儿子，递归左右儿子。

考虑当我们要翻转部分区间的时候，我们这么做显然不对。

但是通过类比的思路，我们能够猜想如果我们对其中一个子树进行如此操作的话是不是就可以了。

那么我们就需要试图找到如此变形后的树：我们要翻转的区间必须全部在一个结点的左儿子侧，且左儿子侧不能有其他多余的点。

为什么这么做呢？思考我们有一个长度为4的区间1 2 3 4，现在要翻转2-3的区间，即变成1 3 2 4

当我们的树变成这样的时候：

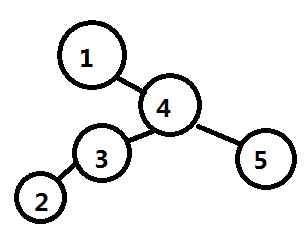
我们以3为对称轴翻转操作得到：

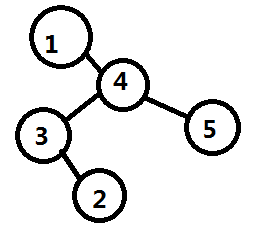
显然我们得到了正确的结果。

所以我们发现当我们要翻转[l,r]的时候，我们只需要通过splay将l-1的点放在root，r+1放在root的儿子处即可。

那么就有一个问题了，假设我们要翻转1-3区间时怎么办？l-1=0，可是我们没有这样的点怎么办？

我们人为添加不就行了？

所以我们加入0结点和n+1结点，这样就可以查询了。

（但是0在splay有很重要的意义，所以本代码将所有的编号往后移动一位）

但是这样的优化远远不够：思考进行了连续多次的修改区间的操作，我们发现后一次修改可能覆盖掉前一次修改，而翻转*2=不翻转，所以我们有了lazy延迟的想法。

我们对于要交换左右儿子的结点打上lazy标记，同时在更新的时候下传即可。

#include<cstdio>
#include<queue>
#include<cctype>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;
const int N=;
inline int read(){
    int X=,w=;char ch=;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch))X=(X<<)+(X<<)+(ch^),ch=getchar();
    return w?-X:X;
}
int fa[N],tr[N][],key[N],size[N];
int root,sz;
bool lazy[N];
inline bool get(int x){
    return tr[fa[x]][]==x;
}
inline void update(int x){
    if(x){
        size[x]=;
        if(tr[x][])size[x]+=size[tr[x][]];
        if(tr[x][])size[x]+=size[tr[x][]];
    }
    return;
}
inline void rotate(int x){
    int old=fa[x],oldf=fa[old],which=get(x);
    tr[old][which]=tr[x][which^];fa[tr[old][which]]=old;
    fa[old]=x;tr[x][which^]=old;fa[x]=oldf;
    if(oldf)tr[oldf][tr[oldf][]==old]=x;
    update(old);update(x);
    return;
}
inline void splay(int x,int y){
    int f=fa[x];
    while(f!=y){
        if(fa[f]!=y)rotate((get(x)==get(f)?f:x));
        rotate(x);f=fa[x];
    }
    if(!y)root=x;
    return;
}
inline void insert(int v){
    sz++;tr[sz][]=tr[sz][]=fa[sz]=;
    key[sz]=v;size[sz]=;
    if(sz==)root=sz;
    else{
        tr[sz-][]=sz;
        fa[sz]=sz-;
        update(fa[sz]);splay(sz,);
    }
    return;
}
inline void pushdown(int x){
    if(!lazy[x])return;
    swap(tr[x][],tr[x][]);
    lazy[tr[x][]]^=;
    lazy[tr[x][]]^=;
    lazy[x]=;
    return;
}
inline int kthmin(int k,int x){
    pushdown(x);
    if(k==+size[tr[x][]])return x;
    else if(k<=size[tr[x][]])return kthmin(k,tr[x][]);
    else return kthmin(k-size[tr[x][]]-,tr[x][]);
}
inline void turn(int l,int r){
    int x=kthmin(l-,root);
    int y=kthmin(r+,root);
    splay(x,);splay(y,x);
    lazy[tr[y][]]^=;
    return;
}
int main(){
    int n=read();
    int m=read();
    for(int i=;i<=n+;i++)insert(i+);
    for(int i=;i<=m;i++){
        int l=read()+;
        int r=read()+;
        turn(l,r);
    }
    for(int i=;i<=n+;i++)printf("%d ",key[kthmin(i,root)]-);
    return ;
}