UVA11951 Area 题解

Content

小 S 想买下一块地。他所在的城市可以看成一个 $n\times m$ 的网格，要购买所处在 $(i,j)$ 的网格需要缴税 $c_{i,j}$ 元，如果一块地里面有多个网格，则所要缴的税为每个网格需要缴税的和。小 S 手头有 $K$ 块钱，他想知道他最多能够买下多大面积的地，并且想知道所有满足要求的地中缴税最少的一块地所要缴的税。注意他能买的一块地只能是一个矩形。

形式化题意： 有一个 $n\times m$ 的矩阵，在 $(i,j)$ 上的元素有一个权值 $c_{i,j}$，你想知道能够选出权值和 $\leqslant K$ 的所有子矩阵中包含最多元素的矩阵的元素个数以及在满足元素个数最大的条件下这个子矩阵中权值和的最小值。

数据范围：$t$ 组数据，$1\leqslant t\leqslant 110$，$1\leqslant n,m\leqslant 10^9$，$1\leqslant K\leqslant 10^9$，$1\leqslant c_{i,j}\leqslant 10^6$。

Solution

思路简单的二维前缀和问题。

我们先通过 $\mathcal O(nm)$ 的复杂度把 $s_{i,j}=\sum\limits_{x=1}^i\sum\limits_{y=1}^j c_{i,j}$ 预处理出来。当然 $\mathcal O(n^2m^2)$ 的暴力计算在本题中貌似也可以，但还是讲讲前缀和怎么处理吧。

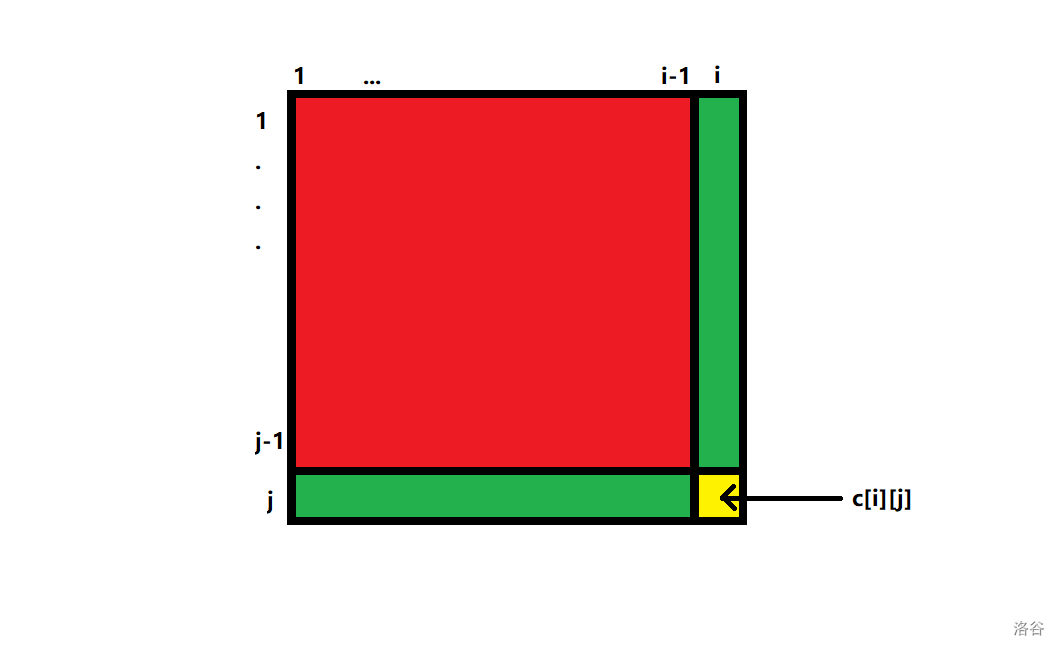
通过这个图我们不难发现，其中红色的部分是 $s_{i-1,j}+s_{i,j-1}$ 而导致的重复的部分，也就是 $s_{i-1,j-1}$，需要减一个。

因此可以很容易推出来 $s_{i,j}=s_{i-1,j}+s_{i,j-1}-s_{i-1,j-1}+c_{i,j}$。

然后我们再直接暴力枚举选取的矩阵的左上角 $(i_1,j_1)$ 和右下角 $(i_2,j_2)$。然后这块地的 $\sum\limits_i\sum\limits_jc_{i,j}$ 的公式推导类似于上面，只不过先要减去两个大的矩阵，再加回去两个矩阵重复减的部分。即为 $s_{i_2,j_2}-s_{i_1-1,j_2}-s_{i_2,j_1-1}+s_{i_1-1,j_1-1}$。面积倒很简单求，就是 $(i_2-i_1+1)(j_2-j_1+1)$。然后拿它和当前的面积最大值进行比较：

如果比当前最大面积小，那就想都不用想，直接跳过。
如果和当前最大面积一样（注意！！！这里如果直接看原题面容易被坑到，这也是我要在翻译里面把要求的东西解释的如此复杂的原因），不要直接跳过，要把这块地的价值和当前的在最大面积下的价值和最小值进行比较，如果比当前的在最大面积下的价值和最小值小的话需要更新！
如果比当前最大面积小，更新面积，并且同时更新价值和最小值（因为现在有了新的最大面积，原来的最大面积下的价值和最小值就得要覆盖）。

最后把求出来的东西输出即可。

Code

int c[107][107];

ll s[107][107];

int main() {

	int t = Rint;

	F(int, test, 1, t) {

		memset(s, 0ll, sizeof(s));

		int n = Rint, m = Rint, ans = 0; ll k = Rll, cost = 0;

		F(int, i, 1, n) F(int, j, 1, m) c[i][j] = Rint;

		F(int, i, 1, n) F(int, j, 1, m) s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + c[i][j];

		F(int, i, 1, n) F(int, j, 1, m) F(int, i2, i, n) F(int, j2, j, m) {

			ll p = s[i2][j2] - s[i - 1][j2] - s[i2][j - 1] + s[i - 1][j - 1];

			if(p <= k) cost = (ans == (i2 - i + 1) * (j2 - j + 1) ? min(cost, p) : (ans < (i2 - i + 1) * (j2 - j + 1) ? p : cost)), ans = max(ans, (i2 - i + 1) * (j2 - j + 1));

		}

		printf("Case #%d: %d %lld\n", test, ans, cost);

	}

    return 0;

}