朴素贝叶斯原理、实例与Python实现

初步理解一下：对于一组输入，根据这个输入，输出有多种可能性，需要计算每一种输出的可能性，以可能性最大的那个输出作为这个输入对应的输出。

那么，如何来解决这个问题呢？

贝叶斯给出了另一个思路。根据历史记录来进行判断。

思路是这样的：

1、根据贝叶斯公式：P（输出|输入）=P（输入|输出）*P（输出）/P（输入）

2、P（输入）=历史数据中，某个输入占所有样本的比例；

3、P（输出）=历史数据中，某个输出占所有样本的比例；

4、P（输入|输出）=历史数据中，某个输入，在某个输出的数量占所有样本的比例，例如：30岁，男性，中午吃面条，其中【30岁，男性就是输入】，【中午吃面条】就是输出。

一、条件概率的定义与贝叶斯公式

二、朴素贝叶斯分类算法

朴素贝叶斯是一种有监督的分类算法，可以进行二分类，或者多分类。一个数据集实例如下图所示：

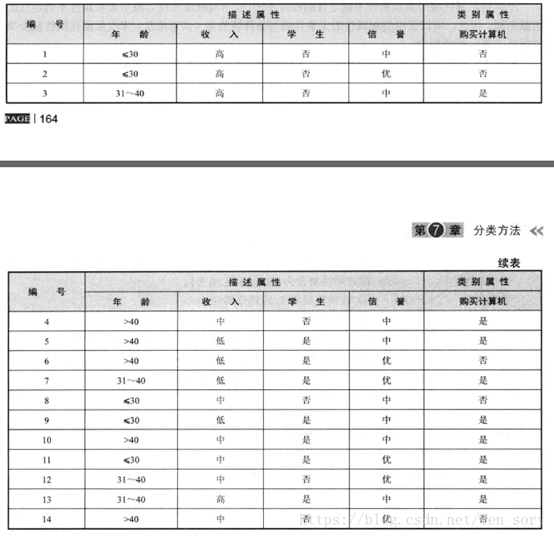
现在有一个新的样本， X = (年龄：<=30, 收入：中， 是否学生：是， 信誉：中)，目标是利用朴素贝叶斯分类来进行分类。假设类别为C(c1=是 或 c2=否)，那么我们的目标是求出P(c1|X)和P(c2|X)，比较谁更大，那么就将X分为某个类。

下面，公式化朴素贝叶斯的分类过程。

三、实例

下面，将下面这个数据集作为训练集，对新的样本X = (年龄：<=30, 收入：中， 是否学生：是， 信誉：中)  作为测试样本，进行分类。

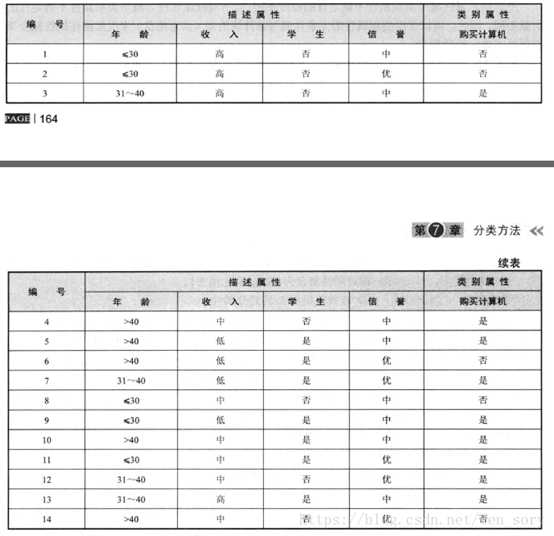
我们可以将这个实例中的描述属性和类别属性，与公式对应起来，然后计算。

参考python实现代码

#coding:utf-8
# 极大似然估计  朴素贝叶斯算法
import pandas as pd
import numpy as np

class NaiveBayes(object):
    def getTrainSet(self):
        dataSet = pd.read_csv('F://aaa.csv')
        dataSetNP = np.array(dataSet)  #将数据由dataframe类型转换为数组类型
        trainData = dataSetNP[:,0:dataSetNP.shape[1]-1]   #训练数据x1,x2
        labels = dataSetNP[:,dataSetNP.shape[1]-1]        #训练数据所对应的所属类型Y
        return trainData, labels

    def classify(self, trainData, labels, features):
        #求labels中每个label的先验概率
        labels = list(labels)    #转换为list类型
        labelset = set(labels)
        P_y = {}       #存入label的概率
        for label in labelset:
            P_y[label] = labels.count(label)/float(len(labels))   # p = count(y) / count(Y)
            print(label,P_y[label])

        #求label与feature同时发生的概率
        P_xy = {}
        for y in P_y.keys():
            y_index = [i for i, label in enumerate(labels) if label == y]  # labels中出现y值的所有数值的下标索引
            for j in range(len(features)):      # features[0] 在trainData[:,0]中出现的值的所有下标索引
                x_index = [i for i, feature in enumerate(trainData[:,j]) if feature == features[j]]
                xy_count = len(set(x_index) & set(y_index))   # set(x_index)&set(y_index)列出两个表相同的元素
                pkey = str(features[j]) + '*' + str(y)
                P_xy[pkey] = xy_count / float(len(labels))
                print(pkey,P_xy[pkey])

        #求条件概率
        P = {}
        for y in P_y.keys():
            for x in features:
                pkey = str(x) + '|' + str(y)
                P[pkey] = P_xy[str(x)+'*'+str(y)] / float(P_y[y])    #P[X1/Y] = P[X1Y]/P[Y]
                print(pkey,P[pkey])

        #求[2,'S']所属类别
        F = {}   #[2,'S']属于各个类别的概率
        for y in P_y:
            F[y] = P_y[y]
            for x in features:
                F[y] = F[y]*P[str(x)+'|'+str(y)]     #P[y/X] = P[X/y]*P[y]/P[X]，分母相等，比较分子即可，所以有F=P[X/y]*P[y]=P[x1/Y]*P[x2/Y]*P[y]
                print(str(x),str(y),F[y])

        features_label = max(F, key=F.get)  #概率最大值对应的类别
        return features_label

if __name__ == '__main__':
    nb = NaiveBayes()
    # 训练数据
    trainData, labels = nb.getTrainSet()
    # x1,x2
    features = [8]
    # 该特征应属于哪一类
    result = nb.classify(trainData, labels, features)
    print(features,'属于',result)

#coding:utf-8
#朴素贝叶斯算法   贝叶斯估计， λ=1  K=2， S=3； λ=1 拉普拉斯平滑
import pandas as pd
import numpy as np

class NavieBayesB(object):
    def __init__(self):
        self.A = 1    # 即λ=1
        self.K = 2
        self.S = 3

    def getTrainSet(self):
        trainSet = pd.read_csv('F://aaa.csv')
        trainSetNP = np.array(trainSet)     #由dataframe类型转换为数组类型
        trainData = trainSetNP[:,0:trainSetNP.shape[1]-1]     #训练数据x1,x2
        labels = trainSetNP[:,trainSetNP.shape[1]-1]          #训练数据所对应的所属类型Y
        return trainData, labels

    def classify(self, trainData, labels, features):
        labels = list(labels)    #转换为list类型
        #求先验概率
        P_y = {}
        for label in labels:
            P_y[label] = (labels.count(label) + self.A) / float(len(labels) + self.K*self.A)

        #求条件概率
        P = {}
        for y in P_y.keys():
            y_index = [i for i, label in enumerate(labels) if label == y]   # y在labels中的所有下标
            y_count = labels.count(y)     # y在labels中出现的次数
            for j in range(len(features)):
                pkey = str(features[j]) + '|' + str(y)
                x_index = [i for i, x in enumerate(trainData[:,j]) if x == features[j]]   # x在trainData[:,j]中的所有下标
                xy_count = len(set(x_index) & set(y_index))   #x y同时出现的次数
                P[pkey] = (xy_count + self.A) / float(y_count + self.S*self.A)   #条件概率

        #features所属类
        F = {}
        for y in P_y.keys():
            F[y] = P_y[y]
            for x in features:
                F[y] = F[y] * P[str(x)+'|'+str(y)]

        features_y = max(F, key=F.get)   #概率最大值对应的类别
        return features_y

if __name__ == '__main__':
    nb = NavieBayesB()
    # 训练数据
    trainData, labels = nb.getTrainSet()
    # x1,x2
    features = [10]
    # 该特征应属于哪一类
    result = nb.classify(trainData, labels, features)
    print(features,'属于',result)

参考链接：

https://blog.csdn.net/ten_sory/article/details/81237169

https://www.cnblogs.com/yiyezhouming/p/7364688.html