Solution -「Gym 102798I」Sean the Cuber

\(\mathcal{Description}\)

  Link.

  给定两个可还原的二阶魔方，求从其中一个状态拧到另一个状态的最小步数。

  数据组数 \(T\le2.5\times10^5\)。

\(\mathcal{Solution}\)

  是这样的，我画了两面草稿纸，顺便手工了一个立体魔方，所以我可以拜访出题人吗？

  先放一张展开图：

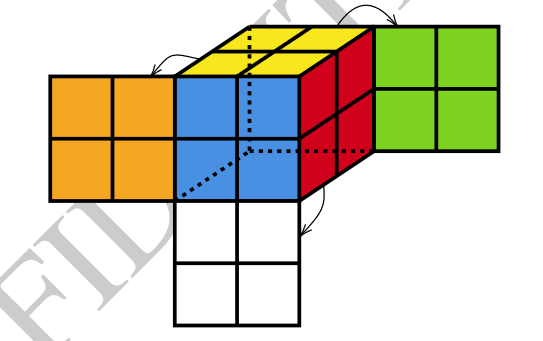
  第一步，给魔方在整体转动的意义下定位。任取一个角块，例如 \((B,R,Y)\)（指由这三种颜色构成的角块，下同），钦定它必须在前方右上角，且蓝色必须朝前。此时能够计算魔方本质不同状态数：其余 \(7\) 个角块任意排列 \(7!\)，每个角块三种状态 \(3^7\)，但当算上 \((B,R,Y)\) 的其中七个角块确定时，剩下的角块只有一种状态能使魔方可还原，所以总状态数为 \(7!\times3^6=3674160\)。这亦提供了一种对已定位魔方的 hash 方法：对于角块排列 Cantor 展开，再算上块的三进制状态。

  第二步，将每个面唯一编号（同色面可以通过所在角块颜色组合确定编号），以还原状态为零元 \(\iota\)，所有可还原状态构成置换群 \((G,\cdot)\)，那么对于两个魔方 \(p,q\)，\(\operatorname{dist}(p,q)=\operatorname{dist}(\iota,p^{-1}q)\)。我们预处理 \(\iota\) 到每种魔方的最短步数就能快速查表求出答案。而由于 \((B,R,Y)\) 固定，可用的转动有 后侧左旋、后侧右旋、左侧左旋、左侧右旋、下侧左旋、下侧右旋六种，分别打出置换表即可。

---

  好吧我来好心地讲一下实现。我对如上图还原魔方的编号方式为：

      20  3
      21  2
19 22 23  0  1  4  5 18
16 13 12 11 10  7  6 17
      14  9
      15  8

总之角块上三个面的编号得连续。设现在输入的魔方置换为 \(p\)，第一步定位过程中，首先若 \(0\) 所在角块不在右侧面，则交换 \(p_i\) 与 \(p_{i+12}\)（整体右旋 \(180°\)）；此后不停整体上旋 \(180°\) 直到 \(0\) 所在角块在右侧上方；最后以右上-左下为轴整体旋转 \(120°\) 直到 \(p_0=0\)，定位完成。

  对于六种转动置换，打三个表，另外三个直接求逆就好√

  其他细节貌似不吓人了，主要是表别打错。

  我所实现的复杂度大概是 \(\mathcal O(3674160\times24\times6+T)\) 叭。

\(\mathcal{Code}\)

/*~Rainybunny~*/

#include <bits/stdc++.h>

#define rep( i, l, r ) for ( int i = l, rep##i = r; i <= rep##i; ++i )
#define per( i, r, l ) for ( int i = r, per##i = l; i >= per##i; --i )

const int MAXS = 3674160;

struct Cube {
    int prm[24];

    Cube() { rep ( i, 0, 23 ) prm[i] = i; }
    Cube( const std::vector<int>& p ) { rep ( i, 0, 23 ) prm[i] = p[i]; }
    Cube( const char* tmp ) {
        static std::map<std::string, int> BLOCK = {
            { "BRY", 0 }, { "YRG", 1 }, { "GRW", 2 }, { "WRB", 3 },
            { "BOW", 4 }, { "WOG", 5 }, { "GOY", 6 }, { "YOB", 7 }
        };
        /* turn into permutation */
        for ( int i = 0; i < 24; i += 3 ) {
            rep ( j, 0, 2 ) {
                std::string cor = { tmp[i + j], tmp[i + ( j + 1 ) % 3],
                  tmp[i + ( j + 2 ) % 3] };
                if ( BLOCK.count( cor ) ) {
                    int v = BLOCK[cor];
                    prm[i + j] = v * 3;
                    prm[i + ( j + 1 ) % 3] = v * 3 + 1;
                    prm[i + ( j + 2 ) % 3] = v * 3 + 2;
                }
            }
        }
        /* adjust it till prm[0]=0 */
        int zpos = 0; while ( prm[zpos] ) ++zpos;
        if ( zpos >= 12 ) { // RR, turn to right side.
            rep ( i, 0, 11 ) prm[i] ^= prm[i + 12] ^= prm[i] ^= prm[i + 12];
            zpos -= 12;
        }
        zpos /= 3; // block id.
        while ( zpos ) { // U till 0 get block 0.
            static int tp[24];
            rep ( i, 0, 11 ) tp[( i + 3 ) % 12] = prm[i];
            rep ( i, 12, 23 ) tp[( i + 9 ) % 12 + 12] = prm[i];
            rep ( i, 0, 23 ) prm[i] = tp[i];
            zpos = ( zpos + 1 ) & 3;
        }
        static const Cube ROT = std::vector<int>{ 1, 2, 0, 23, 21, 22,
            19, 20, 18, 5, 3, 4,
            7, 8, 6, 17, 15, 16,
            13, 14, 12, 11, 9, 10 };
        while ( prm[0] )
            *this = *this * ROT;
    }

    inline int& operator [] ( const int k ) { return prm[k]; }

    inline Cube inv() const {
        static Cube ret;
        rep ( i, 0, 23 ) ret[prm[i]] = i;
        return ret;
    }

    inline Cube operator * ( const Cube& t ) const {
        static Cube ret;
        rep ( i, 0, 23 ) ret[i] = prm[t.prm[i]];
        return ret;
    }

    inline int hash() const {
        static const int fac[7] = { 1, 1, 2, 6, 24, 120, 720 };
        int apr = 127, ret = 0;
        rep ( i, 0, 6 ) { // cantor
            int v = prm[( i + 1 ) * 3] / 3 - 1;
            ret += fac[6 - i] * __builtin_popcount( apr & ( ( 1 << v ) - 1 ) );
            apr ^= 1 << v;
        }
        rep ( i, 1, 6 ) ret = ret * 3 + prm[i * 3] % 3;
        assert( 0 <= ret && ret < MAXS );
        return ret;
    }
};

const Cube TWIST[6] = {
    std::vector<int>{ 0, 1, 2, 7, 8, 6, 17, 15, 16, 9, 10, 11,
      12, 13, 14, 19, 20, 18, 5, 3, 4, 21, 22, 23 }, // BL
    std::vector<int>{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
      21, 22, 23, 12, 13, 14, 15, 16, 17, 18, 19, 20 }, // LD
    std::vector<int>{ 0, 1, 2, 3, 4, 5, 10, 11, 9, 14, 12, 13,
      16, 17, 15, 8, 6, 7, 18, 19, 20, 21, 22, 23 }, // DR
    TWIST[0].inv(),
    TWIST[1].inv(),
    TWIST[2].inv()
};

int dist[MAXS + 5];

inline void init() {
    static std::queue<Cube> que; que.push( Cube() );
    memset( dist, 0xff, sizeof dist ), dist[Cube().hash()] = 0;
    while ( !que.empty() ) {
        Cube u( que.front() ); int hu = u.hash();
        que.pop();
        rep ( i, 0, 5 ) {
            Cube v( u * TWIST[i] ); int hv = v.hash();
            if ( !~dist[hv] ) dist[hv] = dist[hu] + 1, que.push( v );
        }
    }
}

inline void readCubes( Cube& A, Cube& B ) {
    char a[24], b[24], t;
    std::cin >> a[20] >> a[3] >> t >> b[20] >> b[3];
    std::cin >> a[21] >> a[2] >> t >> b[21] >> b[2];
    std::cin >> a[19] >> a[22] >> a[23] >> a[0]
      >> a[1] >> a[4] >> a[5] >> a[18] >> t
      >> b[19] >> b[22] >> b[23] >> b[0]
      >> b[1] >> b[4] >> b[5] >> b[18];
    std::cin >> a[16] >> a[13] >> a[12] >> a[11]
      >> a[10] >> a[7] >> a[6] >> a[17] >> t
      >> b[16] >> b[13] >> b[12] >> b[11]
      >> b[10] >> b[7] >> b[6] >> b[17];
    std::cin >> a[14] >> a[9] >> t >> b[14] >> b[9];
    std::cin >> a[15] >> a[8] >> t >> b[15] >> b[8];
    A = a, B = b;
}

int main() {
    std::ios::sync_with_stdio( false ), std::cin.tie( 0 );

    init();
    std::cerr << "init finished in "
      << double( clock() ) / CLOCKS_PER_SEC << "s\n";
    int T; std::cin >> T;
    while ( T-- ) {
        static Cube u, v; readCubes( u, v );
        std::cout << dist[( u.inv() * v ).hash()] << '\n';
    }
    return 0;
}