Solution Set -「ARC 107」

「ARC 107A」Simple Math

  Link.

  答案为：

\[\frac{a(a+1)\cdot b(b+1)\cdot c(c+1)}{8}
\]

「ARC 107B」Quadruple

  Link.

  枚举 \(i=c+d\)，则 \(a+b=i+k\)，乘法原理计数。

「ARC 107C」Shuffle Permutation

  Link.

  由于矩阵内无相等元素，所以行和列的顺序可以直接乘法原理。以对行的排列方案计数为例，并查集维护所有可以交换位置的行，则行的方案为每个集合大小的阶乘之积。列同理。

「ARC 107D」Number of Multisets

  Link.

  我真的傻了啊这题都想不出来。

  DP，令 \(f(i,j)\) 表示 \(n=i,k=j\) 时的答案。利用当 \(i<j\)，\(f(i,j)=0\) 的边界，有转移：

\[f(i,j)=f(i,2j)+f(i-1,j-1)
\]

  自行理解。复杂度 \(\mathcal O(nk)\)。

「ARC 107E」Mex Mat

  Link.

  结论：\((\forall i,j>4)(a_{ij}=a_{i-1,j-1})\)。手玩一下可以证明。（

  写的时候可以用 std::vector，这样直接在同一个“数组”上二维下标引用会舒服一点。

  复杂度 \(\mathcal O(n)\)。

「ARC 107F」Sum of Abs

  Link.

  首先考虑把绝对值转化一下，对于一个集合 \(\{a\}\)，显然有：

\[|\sum a|=\max\{\sum a,\sum-a\}
\]

  也就是说，一个联通块内的数可以同时取负。

  从数据范围 \(n,m\le300\) 又想到最小割。不妨先获得所有 \(|b_i|\) 的收益，然后建图描述删点的操作。

  一种建图如下（\(b_1\ge 0,b_2<0\)，图中 \(i\) 应为 \(2\)，抱歉 qwq）：

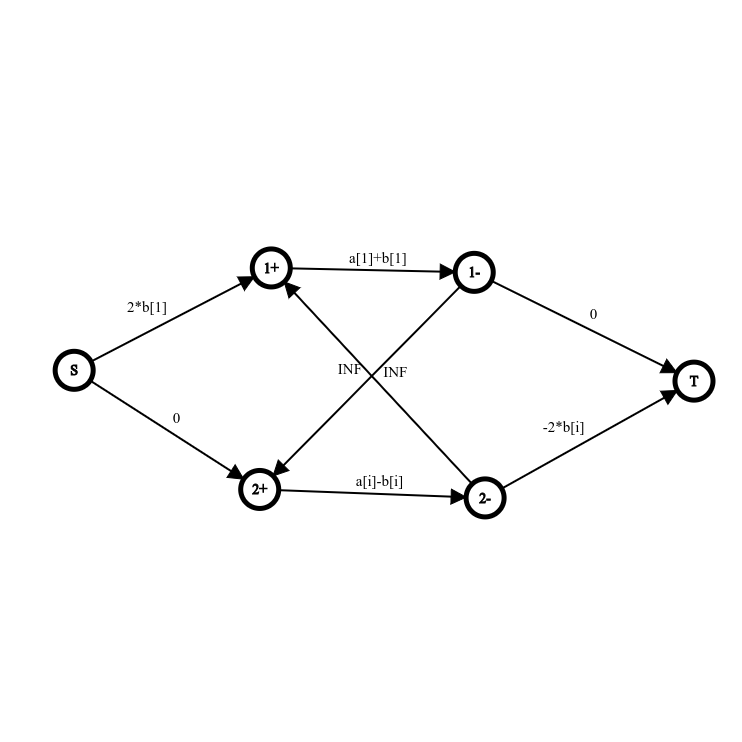
  \(i+\) 表示这个点在联通块中作正贡献，\(i-\) 则相反。割去 \(\langle i+,i-\rangle\) 表示删去点 \(i\)。可以发现，在没有删点的情况下，两个有边相连的点不可能取一正一负，符合要求。