算法打卡|Day1 数组part01

Day1 数组part01

---

今日任务:数组理论基础，704. 二分查找，27. 移除元素

目录

• • Day1 数组part01
  • 今日任务:数组理论基础，704. 二分查找，27. 移除元素
    • Part1: 数组理论基础
    • Problem: 704. 二分查找
• 思路
• 解题方法
• 复杂度
• Code
  • • Problem: 27. 移除元素
• 思路
• 解题方法
• 简单Code
• 暴力Code

---

Part1: 数组理论基础

文章链接：https://programmercarl.com/数组理论基础.html

重点：

1. 数组下标都是从0开始的。
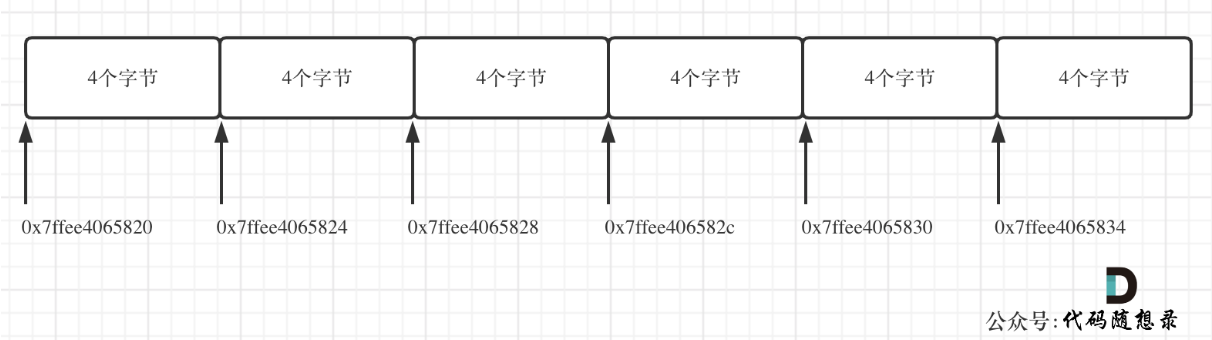
2. 数组内存空间的地址是连续的（在c++中一维数组和二维数组的地址都是连续的）。
   
   

---

Problem: 704. 二分查找

思路

二分法的本质其实就是找两段性质，然后不断更新这两个性质的区间。所以针对二分的的问题我们可以有如下的思路：

解题方法

这里给出一种通用的二分模板解法：

需要特别注意的是，这个代码不适用两个特殊情况，一种就是目标值不在数组中并且比所有值小，一种是目标值步骤数组中并且比所有值大，这两种情况会导致l和r没有更新，因此在输出结果时要检查l，r是否是-1和n（也就是原值），这个在之后的代码叙述。

链接： 1.https://www.bilibili.com/video/BV1d54y1q7k7/?spm_id_from=333.999.0.0&vd_source=90560ea8f1a9d426bcf084887a3f5d66 2.https://blog.csdn.net/WJPnb1/article/details/126360962?spm=1001.2014.3001.5502

复杂度

• 时间复杂度:

时间复杂度的计算并不是计算程序具体运行的时间，而是算法执行语句的次数。

假设总共有n个元素，每次查找的区间大小就是n，n/2，n/4，…，n/2^{k，其中k就是循环的次数，n/2}k >= 1（1最坏的情况，即还剩一个元素），令n/2^k=1，可得k=log2n（以2为底，n的对数），所以时间复杂度可以表示O(log2n)。

• 空间复杂度:

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。

因为变量只创建一次，所以空间复杂度为O(1)。

Code

class Solution {
public:
  int search(vector<int>& nums, int target) {
      int l = -1;
      int r =nums.size();
      while(l + 1 != r){
          int mid = (l+r)/2;
      //以小于等于目标为分界线，搜索第一个不大于目标值的值（代表着有可能是这个值也可能不是）。
          if(nums[mid] <= target) l = mid;
          else r = mid;
      }

      //先过滤掉l为-1的特殊情况，再带入数组下标避免数组越界错误。
      if(l == -1 || nums[l] == target){
          return l;
      } else{
          return -1;
      }
  }
};

---

Problem: 27. 移除元素

思路

1. 首先我们可以用暴力解法，用两个循环遍历整个数组，外层循环找数，每找到一个和目标值相等的数，内层循环就向前移动一位，注意最后要 i--，防止指针越过这一位。

2.我们可以运用快慢指针，慢指针先一个一个移动，目的是保留当前下标，快指针快速移动到非目标值（需要一个判断），并且将非目标值赋值到慢指针处。最后慢指针的下标就是所求数组长度。本题之所以可以用快慢指针，就是因为快指针可以一遍遍历不用回头。

解题方法

快慢双指针算法

简单Code

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
  int removeElement(vector<int>& nums, int val) {
      int slow = 0;
      for(int a :nums){
          if(a!=val){
              nums[slow] = a;
              slow++;
          }
      }
      return slow;
  }
};

暴力Code

class Solution {
public:
  int removeElement(vector<int>& nums, int val) {
      int len = nums.size();
      //数组判空，养成好习惯
      if(len == 0){
          return 0;
      }
      int rlen = len;
      for(int i = 0; i<len; i++){
          if(nums[i] == val){
              for(int j = i+1; j<len; j++){
                  nums[j-1] = nums[j];
              }
              i--;
              rlen--;
          }
      }
      return rlen;
  }
};