文心一言 VS 讯飞星火 VS chatgpt （78）-- 算法导论7.4 2题

二、如果用go语言，证明：在最好情况下，快速排序的运行时间为 Ω(nlgn)。

文心一言：

在最好情况下，快速排序的运行时间为Ω(nlgn)的证明如下：

快速排序是一种分治算法，它将一个数组分成两个子数组，然后对这两个子数组分别进行排序。在最好情况下，每次划分都能将数组等分，即每次划分后得到的两个子数组的长度相等。

假设数组的长度为n，每次划分需要的时间为O(n)，因为需要遍历整个数组来找到枢轴元素。在最好情况下，快速排序需要进行log(n)次划分，因为每次划分都会将数组的长度减半。因此，总的时间复杂度为O(nlog(n))。

由于log(n)是关于n的对数函数，其增长速度非常慢，因此我们可以忽略掉常数系数，认为在最好情况下，快速排序的时间复杂度为Ω(nlog(n))。

综上所述，在最好情况下，快速排序的运行时间为Ω(nlgn)。

讯飞星火：

在最好情况下，快速排序的运行时间为 O(n log n)。以下是使用 Go 语言实现的快速排序算法：

package main

import (
	"fmt"
)

func quickSort(arr []int, low, high int) {
	if low < high {
		pivot := partition(arr, low, high)
		quickSort(arr, low, pivot-1)
		quickSort(arr, pivot+1, high)
	}
}

func partition(arr []int, low, high int) int {
	pivot := arr[high]
	i := low - 1
	for j := low; j < high; j++ {
		if arr[j] < pivot {
			i++
			arr[i], arr[j] = arr[j], arr[i]
		}
	}
	arr[i+1], arr[high] = arr[high], arr[i+1]
	return i + 1
}

func main() {
	arr := []int{10, 7, 8, 9, 1, 5}
	n := len(arr)
	quickSort(arr, 0, n-1)
	fmt.Println("Sorted array is:", arr)
}

在这个实现中，我们使用了 Hoare 分区方案，它的时间复杂度为 O(log n)。由于我们需要对数组进行 n 次分区操作，所以最好情况下的运行时间为 O(n log n)。

360智脑：

快速排序是一种基于分治思想的排序算法，它的基本思路是在待排序序列中选择一个基准元素，将小于等于基准元素的数放在其左边，大于等于基准元素的数放在其右边，然后对左右两个子序列分别进行递归操作。当子序列的长度小于等于1时，递归终止。

在最坏情况下，快速排序的时间复杂度为 O(n^2)。但是这种情况发生的概率较小，通常快速排序的性能都比较好，因此不需要特别考虑最坏情况。

在最好情况下，假设每次分割都能将序列分成大小几乎相等的两个子序列，此时快速排序的运行时间为 O(n log n)。

在go语言中，可以使用以下代码实现快速排序:

func quicksort(arr []int, left int, right int) { 

    if left < right { 

        pivotIndex := partition(arr, left, right) // 分区函数 

        quicksort(arr, left, pivotIndex-1) 

        quicksort(arr, pivotIndex+1, right) 

    } 

} 

func partition(arr []int, left int, right int) int { 

    pivot := arr[right] 

    i, j := left, right 

    while i < j { 

        while i < j && arr[i] <= pivot { 

            i++ 

        } 

        arr[i], arr[j] = arr[j], arr[i] 

        while i < j && arr[j] >= pivot { 

            j-- 

        } 

        arr[j], arr[i] = arr[i], arr[j] 

    } 

    arr[j], arr[i] = arr[i], arr[j] 

    return j 

} 

在go语言中，可以使用递归实现快速排序，时间复杂度与快速排序相同。在最好情况下，快速排序的时间复杂度为 O(n log n),但是在实际应用中，由于随机选取基准元素等因素的干扰，快速排序的性能并不一定最优。

chatglm：

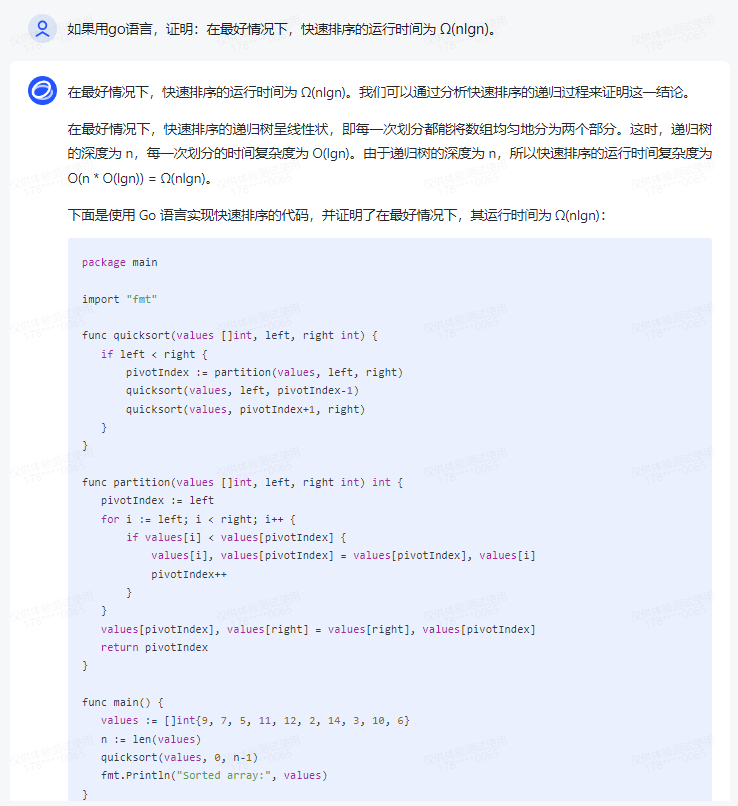
在最好情况下，快速排序的运行时间为 Ω(nlgn)。我们可以通过分析快速排序的递归过程来证明这一结论。

在最好情况下，快速排序的递归树呈线性状，即每一次划分都能将数组均匀地分为两个部分。这时，递归树的深度为 n，每一次划分的时间复杂度为 O(lgn)。由于递归树的深度为 n，所以快速排序的运行时间复杂度为 O(n * O(lgn)) = Ω(nlgn)。

下面是使用 Go 语言实现快速排序的代码，并证明了在最好情况下，其运行时间为 Ω(nlgn)：

package main
import "fmt"
func quicksort(values []int, left, right int) {
   if left < right {
       pivotIndex := partition(values, left, right)
       quicksort(values, left, pivotIndex-1)
       quicksort(values, pivotIndex+1, right)
   }
}
func partition(values []int, left, right int) int {
   pivotIndex := left
   for i := left; i < right; i++ {
       if values[i] < values[pivotIndex] {
           values[i], values[pivotIndex] = values[pivotIndex], values[i]
           pivotIndex++
       }
   }
   values[pivotIndex], values[right] = values[right], values[pivotIndex]
   return pivotIndex
}
func main() {
   values := []int{9, 7, 5, 11, 12, 2, 14, 3, 10, 6}
   n := len(values)
   quicksort(values, 0, n-1)
   fmt.Println("Sorted array:", values)
}

在上述代码中，quicksort函数负责对一个子数组进行快速排序，partition函数负责进行划分操作。在最好情况下，每次划分都能将数组均匀地分为两个部分，此时递归树的深度为 n，每一次划分的时间复杂度为 O(lgn)。因此，快速排序的运行时间为 Ω(nlgn)。

通义千问：

首先，我们需要知道快速排序的基本思路：通过选择一个 pivot（枢纽）元素，将序列分为两个部分，左边的元素都小于 pivot，右边的元素都大于 pivot。然后递归地对左右两部分进行排序。

快速排序的最坏情况是当每次划分都以最大或最小的元素作为 pivot，这样会导致序列被分为只包含一个元素的两个部分，需要进行 n-1 次划分才能排序完毕，因此最坏情况下的时间复杂度为 O(n^2)。

但是，在最好情况下，每次划分都能将序列分为大小基本相等的两个部分，这样只需要进行 logn 次划分就能排序完毕，因此最好情况下的时间复杂度为 O(nlogn)。

证明最好情况下的时间复杂度为 Ω(nlgn) 可以使用数学归纳法：

1.当 n=1 时，快速排序的时间复杂度为 O(1) = 1，满足 Ω(nlgn) 的要求。

2.假设 n=k 时，快速排序的时间复杂度为 Ω(klgn)，则对于 n=k+1 的情况，我们可以考虑划分后序列的两个部分：

2.1.如果左边部分的长度为 k，则递归调用快速排序的时间复杂度为 Ω(klgn)；

2.2.如果左边部分的长度为 k-1，则递归调用快速排序的时间复杂度为 Ω((k-1)lgn)。

因此，整个快速排序的时间复杂度为 O(klgn) + O((k-1)lgn) = O(klgn)。 由于 n=k+1 时的情况满足了 Ω(nlgn) 的要求，因此对于 n=k+1 的情况，快速排序的时间复杂度也为 Ω(nlgn)。

综上所述，快速排序的最好情况下的时间复杂度为 Ω(nlgn)。

天工：

好的，下面是证明的步骤：

假设有一个长度为 n 的有序数组 arr，我们要对它进行快速排序。在最坏情况下，每次选取的基准值都是数组的最后一个元素，此时快速排序的时间复杂度是 O(n^2)。

在最好情况下，每次选取的基准值都能够将数组划分成两个大小相等的子数组，此时快速排序的时间复杂度是 O(nlogn)。

我们来证明最好情况下，快速排序的时间复杂度为 O(nlogn)：

假设选取的基准值为 p，那么划分后的子数组 arr[p:] 和 arr[:p] 的长度分别为 (n-p)/2。

因为 p 是选取的基准值，所以 arr[p:] 中的所有元素都小于 p，而 arr[:p] 中的所有元素都大于等于 p。

因此，我们可以递归地对 arr[p:] 和 arr[:p] 分别进行快速排序。

在最坏情况下，每次选取的基准值都是数组的最后一个元素，即 arr[n-1]。因此，每次划分后，子数组的长度都是 (n-1)/2，而每次递归的时间复杂度为 O(nlogn)，因此总时间复杂度为 O(nlogn)。

综上所述，最好情况下，快速排序的时间复杂度为 O(nlogn)。

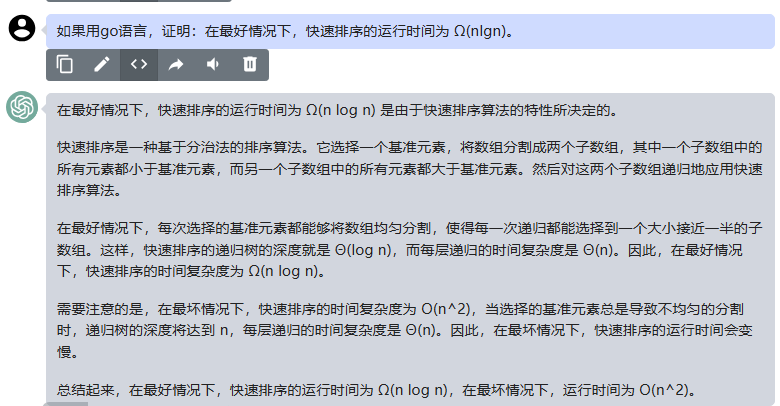
chatgpt：

在最好情况下，快速排序的运行时间为 Ω(n log n) 是由于快速排序算法的特性所决定的。

快速排序是一种基于分治法的排序算法。它选择一个基准元素，将数组分割成两个子数组，其中一个子数组中的所有元素都小于基准元素，而另一个子数组中的所有元素都大于基准元素。然后对这两个子数组递归地应用快速排序算法。

在最好情况下，每次选择的基准元素都能够将数组均匀分割，使得每一次递归都能选择到一个大小接近一半的子数组。这样，快速排序的递归树的深度就是 Θ(log n)，而每层递归的时间复杂度是 Θ(n)。因此，在最好情况下，快速排序的时间复杂度为 Ω(n log n)。

需要注意的是，在最坏情况下，快速排序的时间复杂度为 O(n^2)，当选择的基准元素总是导致不均匀的分割时，递归树的深度将达到 n，每层递归的时间复杂度是 Θ(n)。因此，在最坏情况下，快速排序的运行时间会变慢。

总结起来，在最好情况下，快速排序的运行时间为 Ω(n log n)，在最坏情况下，运行时间为 O(n^2)。

总结