沃罗诺伊图 (Voronoi diagram)

沃罗诺伊图 (Voronoi diagram)

Introduction: what is voronoi diagram?

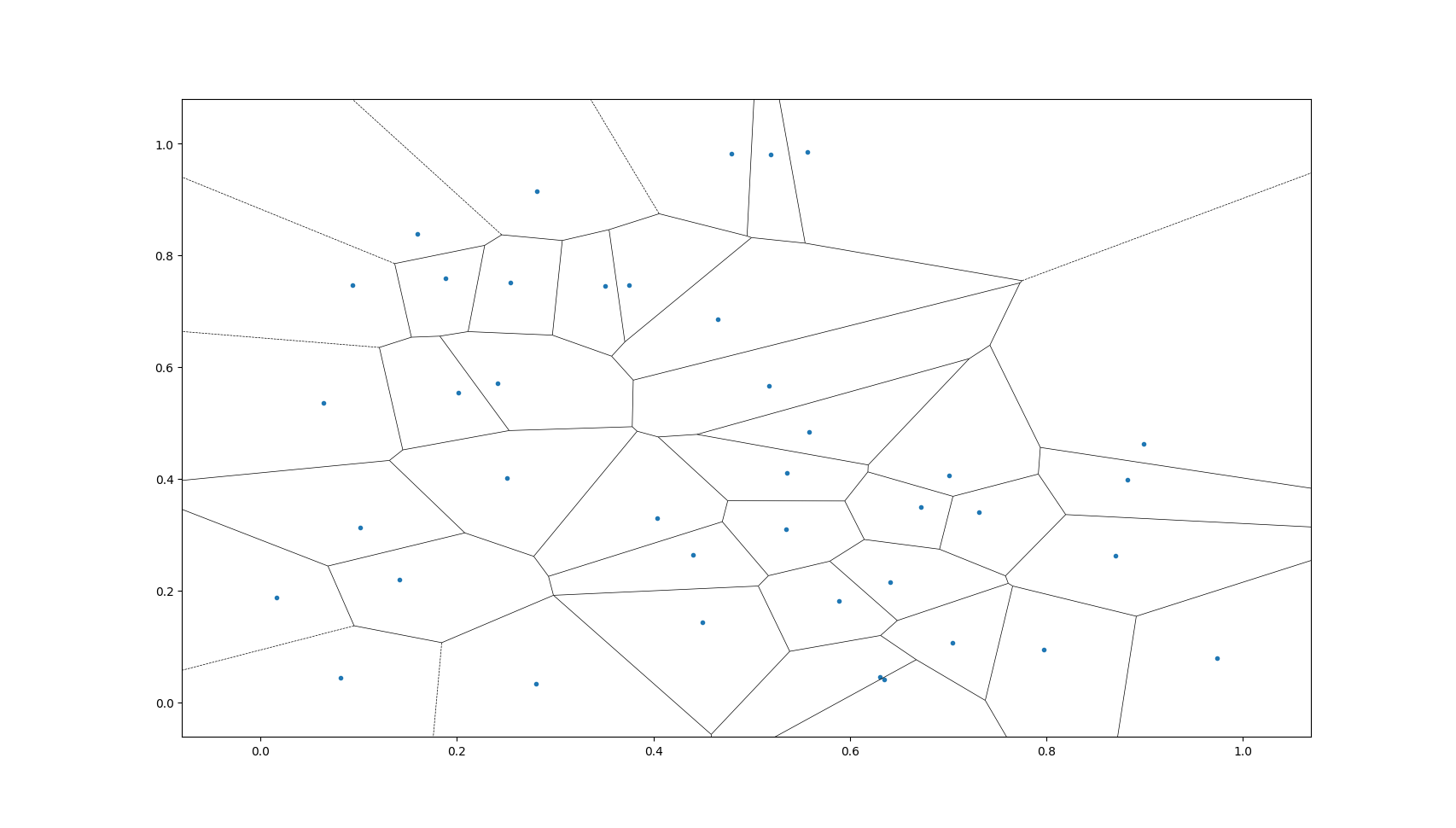
沃罗诺伊图 (Voronoi diagram)，取名自俄罗斯数学家乔治·沃罗诺伊（Georgy Voronoi）。这是一个自然界中经常出现的简单的数学震撼(笑)，在科学技术领域也有许许多多的应用（图像处理、路径规划..好像是）

以上面的Voronoi diagram为例，图上有40个随机放置的核（nucleus），以及围住这些点的区域（Region）.一眼之下，这些图好像杂乱无章，没有什么规律可寻。但是仔细观察可以发现，Region围住的点离各自的核最接近。

Voronoi diagram的特点是：每一个Region围住的点都是离各自Nucleus最近的点。 在图上随便找一个位置，你将会发现这个位置到所属Nucleus的直线距离不会大于到达其余任意一个Nucleus的直线距离。

绘制

现在我们有了Voronoi diagram的明确定义，可以开始绘制它了。然而我们不能直接入手去绘制图像本身，而应该先绘制核的德劳内三角剖分（Delaunay triangulation）。Delaunay triangulation是指用图上的点作为三角形的顶点构造一组三角形，使其满足没有任何一个顶点落在其它三角形的外接圆内

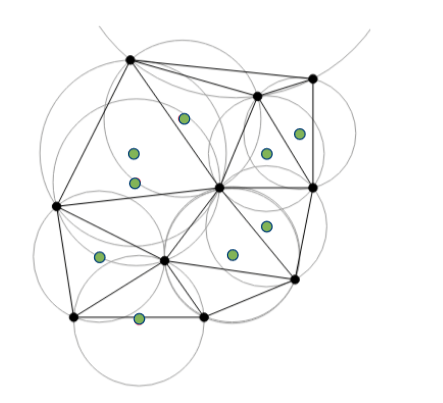
上图中有10个随机分布的黑点，黑色三角即为Delaunay triangulation，绿色点为外接圆的圆心。仔细比对可以发现确实没有任何一个顶点落在别的三角形的外接圆内捏。

那么Delaunay triangulaltion和Voronoi diagram有什么联系呢？我们看同一组随机点的Voronoi diagram和Delaunay triangulation长啥样

仔细观测..脑补右侧图中三角形的外接圆..会发现Voronoi diagram中所有线段交战都恰好对应于Delaunay triangulation外接圆的一个圆心！这就是为什么我们需要先绘制出Delaunay triangulation.

Python

...哇，Python就像是一个究极傻瓜相机

import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import Voronoi,voronoi_plot_2d

np.random.seed()
points=np.random.rand(40,2)

vor=Voronoi(points)

voronoi_plot_2d(vor,show_points=True,show_vertices=False,line_width=0.5)

plt.show()

就画好一个Voronoi diagram了。（具体可参照Scipy官方的Voronoi、voronoi_plot_2d）