Codeforces 711D Directed Roads - 组合数学

ZS the Coder and Chris the Baboon has explored Udayland for quite some time. They realize that it consists of n towns numbered from1 to n.

There are n directed roads in the Udayland. i-th of them goes from town i to some other town ai (ai ≠ i). ZS the Coder can flip the direction of any road in Udayland, i.e. if it goes from town A to town B before the flip, it will go from town B to town A after.

ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns A1, A2, ..., Ak (k > 1) such that for every 1 ≤ i < k there is a road from town Ai to town Ai + 1 and another road from town Ak to town A1. In other words, the roads are confusing if some of them form a directed cycle of some towns.

Now ZS the Coder wonders how many sets of roads (there are 2n variants) in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.

Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.

Input

The first line of the input contains single integer n (2 ≤ n ≤ 2·105) — the number of towns in Udayland.

The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n, ai ≠ i), ai denotes a road going from town i to town ai.

Output

Print a single integer — the number of ways to flip some set of the roads so that the resulting whole set of all roads is not confusing. Since this number may be too large, print the answer modulo 109 + 7.

Examples

input

3
2 3 1

output

6

input

4
2 1 1 1

output

8

input

5
2 4 2 5 3

output

28

Note

Consider the first sample case. There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are , , initially. Number the roads 1 to 3 in this order.

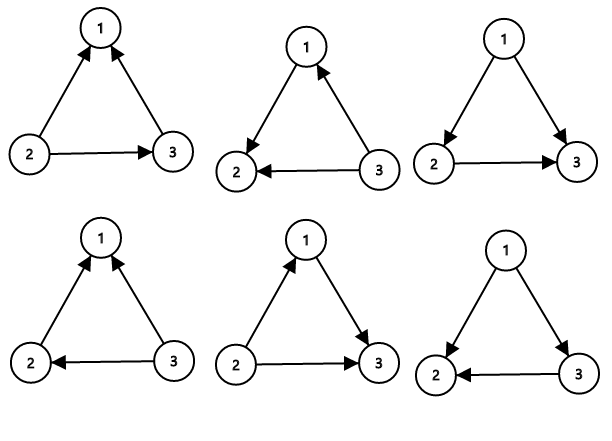
The sets of roads that ZS the Coder can flip (to make them not confusing) are {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Note that the empty set is invalid because if no roads are flipped, then towns 1, 2, 3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.

The sample image shows all possible ways of orienting the roads from the first sample such that the network is not confusing.

---

题目大意

　　给定一个有向图，每个点的出度为1。有一种操作可以将一条边的方向翻转，问有多少种不同的操作方案使得操作后图中不存在点数大于1的强连通分量。

　　因为图很特殊，所以有比较特殊的计算方法。

　　容易发现，对于已经存在的强连通分量，只有全部翻转中间的边和什么都不做的量两种方案不可行，其他都可行。

　　对于不在强连通分量内的边，可翻转也可以不翻转。

　　然后用dfs找环，用乘法原理乘一乘就好。

Code

 /**
  * Codeforces
  * Problem#711D
  * Accepted
  * Time: 62ms
  * Memory: 4376k
  */
 #include <bits/stdc++.h>
 using namespace std;

 const int M = 1e9 + ;

 int n;
 int cnt = ;
 int ric = ;
 int *suf;
 int *vid;
 int *bel;

 int qpow(int a, int pos) {
     int rt = , pa = a;
     for (; pos; pos >>= , pa = pa * 1ll * pa % M)
         if (pos & )
             rt = rt * 1ll * pa % M;
     return rt;
 }

 inline void init() {
     scanf("%d", &n);
     suf = new int[(n + )];
     vid = new int[(n + )];
     bel = new int[(n + )];
     for (int i = ; i <= n; i++)
         scanf("%d", suf + i);
     memset(vid, , sizeof(int) * (n + ));
     memset(bel, , sizeof(int) * (n + ));
 }

 int dfs(int node, int id) {
     vid[node] = ++cnt;
     bel[node] = id;
     int e = suf[node];
     if (vid[e])
         return (bel[e] == id) ? (vid[node] - vid[e] + ) : ();
     return dfs(e, id);
 }

 int ans = ;
 inline void solve() {
     for (int i = , s; i <= n; i++)
         if (!vid[i]) {
             s = dfs(i, i);
             if(s)
                 ans = (ans * 1ll * ((qpow(, s) + M - ) % M)) % M;
             ric += s;
         }
     ans = (ans * 1ll * qpow(, n - ric)) % M;
     printf("%d\n", ans);
 }

 int main() {
     init();
     solve();
     return ;
 }