机器学习笔记——t分布知识点总结

(原创文章，转载请注明地址:http://www.cnblogs.com/wangkundentisy/p/6539058.html )

1.t分布式统计分布的一种，同卡方分布(χ2分布)、F分布并称为三大分布。

2. t分布又叫student-t分布，常常用于根据小样本来估计呈正态分布且方差值为知的样本的均值。（如果总体的方差已知的话，则应该用正态分布来估计总体的均值。）(所以一个前提是：t分布的样本的总体必须符合正态分布)

3.t分布一般用于小样本(样本量比较小)的情形。

4.假设X服从标准正态分布即X~N(0,1)，Y服从自由度n的卡方分布即Y~χ2（n），且X与Y是相互独立的，那么Z=X/sqrt(Y/n)的分布成为自由的为n的t分布，记为Z~t(n).

5.对于Z~t(n)，其数学期望E(Z) = 0，n>1;方差D(Z)=n/n-2 , n>2 。

6.特征：

(1)．以0为中心，左右对称的单峰分布；

(2)．t分布是一簇曲线，其形态变化与n（即其自由度）大小有关。自由度n越小，t分布曲线越低平；自由度n越大，t分布曲线越接近标准正态分布（u分布）曲线，当自由度无限大时，t分布就成了正态分布，如图.

t(n)分布与其密度函数。

(3).随着自由度逐渐增大，t分布逐渐接近标准正态分布。

对应于每一个自由度df，就有一条t分布曲线，每条曲线都有其曲线下统计量t的分布规律，计算较复杂。学生的t分布（或也t分布） ，在概率统计中，在置信区间估计、显著性检验等问题的计算中发挥重要作用。

7.详述：

假设{\displaystyle X}是呈正态分布的独立的随机变量（随机变量的期望值是{\displaystyle \mu }，方差是{\displaystyle \sigma ^{2}}但未知）。 令：

{\displaystyle {\overline {X}}_{n}=(X_{1}+\cdots +X_{n})/n}

为样本均值。

{\displaystyle {S_{n}}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}\left(X_{i}-{\overline {X}}_{n}\right)^{2}}

为样本方差。

它显示了数量

{\displaystyle Z={\frac {{\overline {X}}_{n}-\mu }{\sigma /{\sqrt {n}}}}}

呈正态分布并且均值和方差分别为0和1。

另一个相关数量

{\displaystyle T={\frac {{\overline {X}}_{n}-\mu }{S_{n}/{\sqrt {n}}}}}

T的概率密度函数是：

{\displaystyle f(t)={\frac {\Gamma ((\nu +1)/2)}{{\sqrt {\nu \pi \,}}\,\Gamma (\nu /2)}}(1+t^{2}/\nu )^{-(\nu +1)/2}}

{\displaystyle \nu } 等于n − 1。 T的分布称为t-分布。参数{\displaystyle \nu } 一般被称为自由度。

{\displaystyle \Gamma } 是伽马函数。 如果{\displaystyle \nu }是偶数,

{\displaystyle {\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}={\frac {(\nu -1)(\nu -3)\cdots 5\cdot 3}{2{\sqrt {\nu }}(\nu -2)(\nu -4)\cdots 4\cdot 2\,}}\cdot }

如果{\displaystyle \nu }是奇数,

{\displaystyle {\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}={\frac {(\nu -1)(\nu -3)\cdots 4\cdot 2}{\pi {\sqrt {\nu }}(\nu -2)(\nu -4)\cdots 5\cdot 3\,}}\cdot \!}

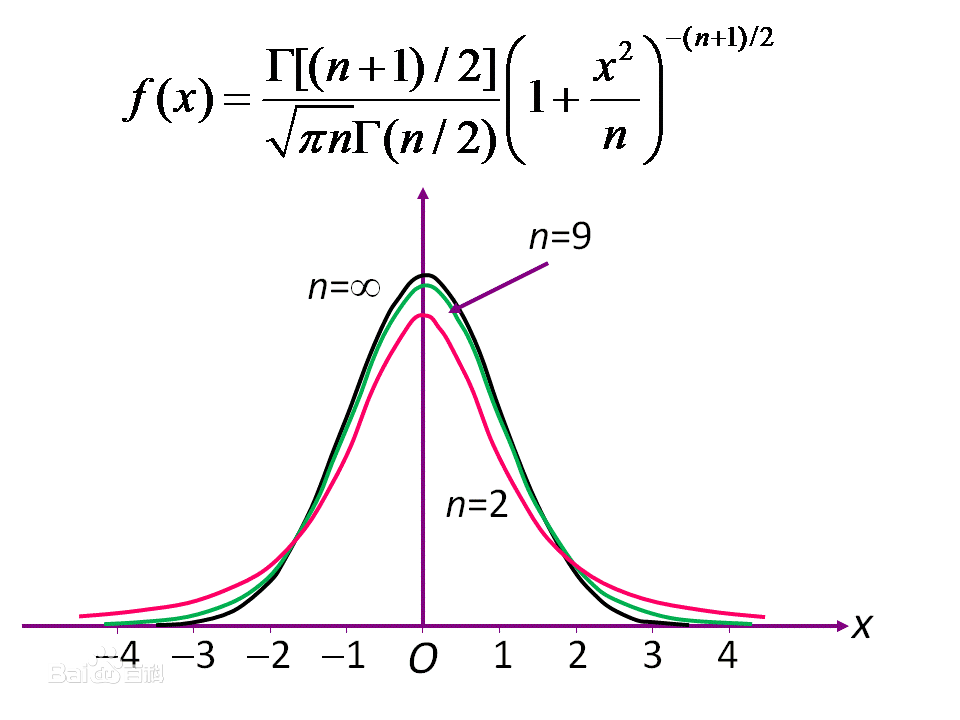
T的概率密度函数的形状类似于均值为0方差为1的正态分布，但更低更宽。随着自由度{\displaystyle \nu }的增加，则越来越接近均值为0方差为1的正态分布。

8.t分布置信区间的推导：

假设数量A在当T呈t-分布（T的自由度为n − 1）满足

{\displaystyle \Pr(-A<T<A)=0.90\,}

这与

{\displaystyle \Pr(T<A)=0.95\,}是相同的

A是这个概率分布的第95个百分点

那么

{\displaystyle \Pr \left(-A<{{\overline {X}}_{n}-\mu \over S_{n}/{\sqrt {n}}}<A\right)=0.9,}

等价于

{\displaystyle \Pr \left({\overline {X}}_{n}-A{S_{n} \over {\sqrt {n}}}<\mu <{\overline {X}}_{n}+A{S_{n} \over {\sqrt {n}}}\right)=0.9}

因此μ的90%置信区间为：

9.分布表格的用法

下表列出了自由度为v 的t-分布的单侧和双侧区间值。例如，当样本数量n=5时，则自由度v=4，我们就可以查找表中以4开头的行。该行第5列值为2.132，对应的单侧值为95%（双侧值为90%）。这也就是说，T小于2.132的概率为95%（即单侧），记为Pr(−∞ < T < 2.132) = 0.95；同时，T值介于-2.132和2.132之间的概率为90%（即双侧），记为Pr(−2.132 < T < 2.132) = 0.9。

这是根据分布的对称性计算得到的，

Pr(T < −2.132) = 1 − Pr(T > −2.132) = 1 − 0.95 = 0.05,

因此，

Pr(−2.132 < T < 2.132) = 1 − 2(0.05) = 0.9.

注意关于表格的最后一行的值：自由度为无限大的t-分布和正态分布等价。

单侧	75%	80%	85%	90%	95%	97.5%	99%	99.5%	99.75%	99.9%	99.95%
双侧	50%	60%	70%	80%	90%	95%	98%	99%	99.5%	99.8%	99.9%
1	1.000	1.376	1.963	3.078	6.314	12.71	31.82	63.66	127.3	318.3	636.6
2	0.816	1.061	1.386	1.886	2.920	4.303	6.965	9.925	14.09	22.33	31.60
3	0.765	0.978	1.250	1.638	2.353	3.182	4.541	5.841	7.453	10.21	12.92
4	0.741	0.941	1.190	1.533	2.132	2.776	3.747	4.604	5.598	7.173	8.610
5	0.727	0.920	1.156	1.476	2.015	2.571	3.365	4.032	4.773	5.893	6.869
6	0.718	0.906	1.134	1.440	1.943	2.447	3.143	3.707	4.317	5.208	5.959
7	0.711	0.896	1.119	1.415	1.895	2.365	2.998	3.499	4.029	4.785	5.408
8	0.706	0.889	1.108	1.397	1.860	2.306	2.896	3.355	3.833	4.501	5.041
9	0.703	0.883	1.100	1.383	1.833	2.262	2.821	3.250	3.690	4.297	4.781
10	0.700	0.879	1.093	1.372	1.812	2.228	2.764	3.169	3.581	4.144	4.587
11	0.697	0.876	1.088	1.363	1.796	2.201	2.718	3.106	3.497	4.025	4.437
12	0.695	0.873	1.083	1.356	1.782	2.179	2.681	3.055	3.428	3.930	4.318
13	0.694	0.870	1.079	1.350	1.771	2.160	2.650	3.012	3.372	3.852	4.221
14	0.692	0.868	1.076	1.345	1.761	2.145	2.624	2.977	3.326	3.787	4.140
15	0.691	0.866	1.074	1.341	1.753	2.131	2.602	2.947	3.286	3.733	4.073
16	0.690	0.865	1.071	1.337	1.746	2.120	2.583	2.921	3.252	3.686	4.015
17	0.689	0.863	1.069	1.333	1.740	2.110	2.567	2.898	3.222	3.646	3.965
18	0.688	0.862	1.067	1.330	1.734	2.101	2.552	2.878	3.197	3.610	3.922
19	0.688	0.861	1.066	1.328	1.729	2.093	2.539	2.861	3.174	3.579	3.883
20	0.687	0.860	1.064	1.325	1.725	2.086	2.528	2.845	3.153	3.552	3.850
21	0.686	0.859	1.063	1.323	1.721	2.080	2.518	2.831	3.135	3.527	3.819
22	0.686	0.858	1.061	1.321	1.717	2.074	2.508	2.819	3.119	3.505	3.792
23	0.685	0.858	1.060	1.319	1.714	2.069	2.500	2.807	3.104	3.485	3.767
24	0.685	0.857	1.059	1.318	1.711	2.064	2.492	2.797	3.091	3.467	3.745
25	0.684	0.856	1.058	1.316	1.708	2.060	2.485	2.787	3.078	3.450	3.725
26	0.684	0.856	1.058	1.315	1.706	2.056	2.479	2.779	3.067	3.435	3.707
27	0.684	0.855	1.057	1.314	1.703	2.052	2.473	2.771	3.057	3.421	3.690
28	0.683	0.855	1.056	1.313	1.701	2.048	2.467	2.763	3.047	3.408	3.674
29	0.683	0.854	1.055	1.311	1.699	2.045	2.462	2.756	3.038	3.396	3.659
30	0.683	0.854	1.055	1.310	1.697	2.042	2.457	2.750	3.030	3.385	3.646
40	0.681	0.851	1.050	1.303	1.684	2.021	2.423	2.704	2.971	3.307	3.551
50	0.679	0.849	1.047	1.299	1.676	2.009	2.403	2.678	2.937	3.261	3.496
60	0.679	0.848	1.045	1.296	1.671	2.000	2.390	2.660	2.915	3.232	3.460
80	0.678	0.846	1.043	1.292	1.664	1.990	2.374	2.639	2.887	3.195	3.416
100	0.677	0.845	1.042	1.290	1.660	1.984	2.364	2.626	2.871	3.174	3.390
120	0.677	0.845	1.041	1.289	1.658	1.980	2.358	2.617	2.860	3.160	3.373
	0.674	0.842	1.036	1.282	1.645	1.960	2.326	2.576	2.807	3.090	3.291

 

 

{\displaystyle {\overline {X}}_{n}\pm A{\frac {S_{n}}{\sqrt {n}}}}