BZOJ.1016.[JSOI2008]最小生成树计数(Matrix Tree定理 Kruskal)

题目链接

最小生成树有两个性质：

1.在不同的MST中某种权值的边出现的次数是一定的。

2.在不同的MST中，连接完某种权值的边后，形成的连通块的状态是一样的。

\(Solution1\)

由这两个性质，可以先求一个MST，再枚举每一组边(权值相同的看做一组边)，对每组边DFS(\(O(2^{10})\))，若某种方案连通性同MST相同(记录连通块个数即可)。则sum++。

最后根据乘法原理，最后的答案即为所有sum相乘。

\(Solution2\)

容易想到MatrixTree定理。

按边权从小到大处理每一组边，在加入这组边之前，之前的边会构成一些连通块，而这组边会一定会将某些连通块连在一起，如下图(我也不知道这图到底是哪的了)：



把之前形成的每个连通块看做一个点，这样又成了一个生成树计数，生成树个数即为该种权值的边的方案数。如下图：



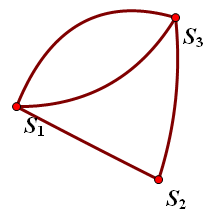
根据乘法原理，我们只要计算出每组边的这个方案，再乘起来就行了。

//920kb	68ms
#include <cstdio>
#include <cctype>
#include <vector>
#include <cstring>
#include <algorithm>
#define gc() getchar()
#define mod (31011)
const int N=102,M=1002;
int n,m,A[N][N],tmp[N][N],fa[N],bel[N],Ans;
bool vis[N];
std::vector<int> v[N];
struct Edge{
	int fr,to,val;
	bool operator <(const Edge &a)const{
		return val<a.val;
	}
}e[M];
inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
int Get_fa(int x,int *f){//两个并查集，一个维护MST中的连通性，一个维护所属连通块。
	return x==f[x]?x:f[x]=Get_fa(f[x],f);
}
void Gauss(int n)
{
	for(int i=1; i<n; ++i)
		for(int j=1; j<n; ++j) (A[i][j]+=mod)%=mod;//!
	bool f=0;
	for(int j=1; j<n; ++j)
	{
		for(int i=j+1; i<n; ++i)
			while(A[i][j])
			{
				int t=A[j][j]/A[i][j];
				for(int k=j; k<n; ++k) A[j][k]=(A[j][k]-t*A[i][k]%mod+mod)%mod;
				for(int k=j; k<n; ++k) std::swap(A[i][k],A[j][k]);
				f^=1;
			}
		if(!A[j][j]) {Ans=0; break;}
		Ans=Ans*A[j][j]%mod;
	}
	if(f) Ans=mod-Ans;//!
}
void Calc()
{
	for(int i=1; i<=n; ++i)
		if(vis[i]) v[Get_fa(i,bel)].push_back(i),vis[i]=0;//处理出每个连通块所含的点(原先连通块的代表元素)。
	for(int x=1; x<=n; ++x)
		if(v[x].size()>1)
		{
			memset(A,0,sizeof A);
			for(int i=0,lim=v[x].size(); i<lim; ++i)
				for(int a=v[x][i],b,j=i+1; j<lim; ++j)
				{
					b=v[x][j];
					if(tmp[a][b]){//tmp[][]作为边矩阵可以不清空，因为这俩连通块不会再同时出现了。
						A[i][j]=A[j][i]=-tmp[a][b];
						A[i][i]+=tmp[a][b], A[j][j]+=tmp[a][b];
					}
				}
			Gauss(v[x].size());
		}
	for(int i=1; i<=n; ++i)
		v[i].clear(), bel[i]=fa[i]=Get_fa(i,bel);//计算完某种边后把同一连通块的缩起来。
}
int main()
{
	n=read(),m=read();
	for(int i=1; i<=m; ++i) e[i].fr=read(),e[i].to=read(),e[i].val=read();
	std::sort(e+1,e+1+m);
	for(int i=1; i<=n; ++i) fa[i]=bel[i]=i;
	e[0].val=e[1].val, Ans=1;
	for(int r1,r2,i=1; i<=m; ++i)
	{
		if(e[i].val!=e[i-1].val) Calc();
		r1=Get_fa(e[i].fr,fa), r2=Get_fa(e[i].to,fa);
		if(r1==r2) continue;
//		fa[r1]=r2;//暂时先不连接。
		vis[r1]=vis[r2]=1;
		++tmp[r1][r2], ++tmp[r2][r1];//, ++tmp[r1][r1], ++tmp[r2][r2];//点的度数矩阵可以之后根据边处理，tmp[][]用来做边矩阵。最好这样，可以不清空。
		bel[Get_fa(e[i].fr,bel)]=Get_fa(e[i].to,bel);//统计出每个连通块。
	}
	Calc();//the last edge
	for(int i=1; i<n; ++i)
		if(bel[i]!=bel[i+1]) {Ans=0; break;}
	printf("%d",Ans);
	return 0;
}