子序列的按位或 Bitwise ORs of Subarrays

2018-09-23 19:05:20

问题描述：

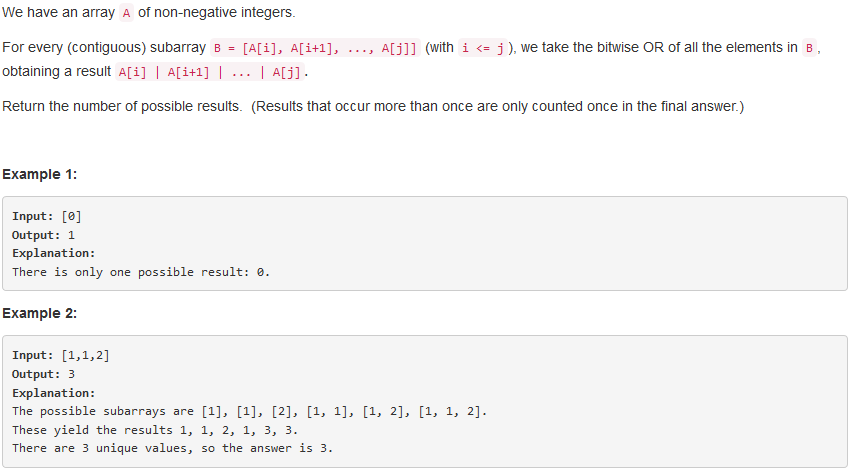
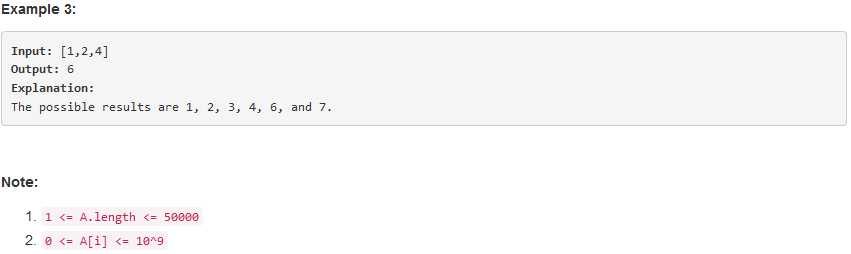
问题求解：

显然的是暴力的遍历所有的区间是不可取的，因为这样的时间复杂度为n^2级别的，对于规模在50000左右的输入会TLE。

然而，最后的解答也可以看作是一个暴力求解，也就是用Set来保存以当前数为结尾的左右可能解，在下一轮中遍历上一轮的所有解并进行或操作。

这里有个难以一下想到的地方就是，乍一看，这个时间复杂度依然是平方级别的，但是实际上，这里的时间复杂度是n级别的，因为Set中后一个数中的1完全覆盖前一个数，因此，最多只有不超过30个数在Set中，因此整个时间复杂度依然是线性的时间复杂度。

    public int subarrayBitwiseORs(int[] A) {
        Set<Integer> res = new HashSet<>();
        Set<Integer> cur = new HashSet<>();
        for (int i : A) {
            Set<Integer> tmp = new HashSet<>();
            tmp.add(i);
            for (Integer j : cur) tmp.add(i | j);
            res.addAll(tmp);
            cur = tmp;
        }
        return res.size();
    }