HDU 6050 17多校2 Funny Function（数学+乘法逆元）

Problem Description

Function Fx,ysatisfies:

For given integers N and M,calculate Fm,1 modulo 1e9+7.

 

Input

There is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.

 

Output

For each given N and M,print the answer in a single line.

 

Sample Input

2

2 2

3 3

 

Sample Output

2

33

数学题，反正我不会。。。数学基础太差了，直接用大佬的数学公式写的

参考博客：http://www.cnblogs.com/Just--Do--It/p/7248089.html

主要是学到了取余和除的话需要求逆元！！可以用费马小定理求，目前我只会这个

继续加油！

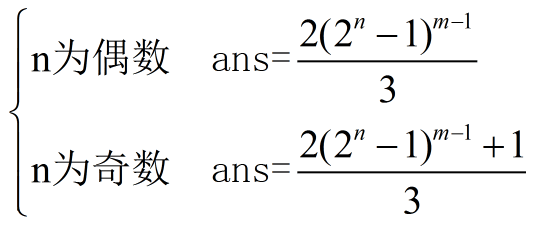
 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<string.h>
 #include<cmath>
 #include<math.h>
 using namespace std;

 #define MOD 1000000000+7

 long long quick_mod(long long a,long long b)//快速幂，复杂度log2n
 {
     long long ans=;
     while(b)
     {
         if(b&)
         {
             ans*=a;
             ans%=MOD;
             b--;
         }
         b/=;
         a*=a;
         a%=MOD;
     }
     return ans;
 }

 long long inv(long long x)
 {
     return quick_mod(x,MOD-);//根据费马小定理求逆元，3*（3^(mod-2)）=1
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     long long n,m,ans;
     while(T--)
     {
         scanf("%lld%lld",&n,&m);
         if(n%==)
             ans=(quick_mod(quick_mod(,n)-,m-)*)*inv();
         else
             ans=(quick_mod(quick_mod(,n)-,m-)*+)*inv();
         ans%=MOD;
         printf("%lld\n",ans);
     }
     return true;
 }