SciPy模块应用

1.图像模糊

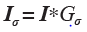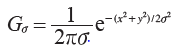 图像的高斯模糊是非常经典的图像卷积例子。本质上，图像模糊就是将（灰度）图像I 和一个高斯核进行卷积操作：，其中是标准差为σ的二维高斯核。高斯模糊通常是其他图像处理操作的一部分，比如图像插值操作、兴趣点计算以及很多其他应用。SciPy 有用来做滤波操作的scipy.ndimage.filters 模块。该模块使用快速一维分离的方式来计算卷积。eg：

from PIL import Image
from numpy import *
from scipy.ndimage import filters
im = array(Image.open('empire.jpg').convert('L'))
im2 = filters.gaussian_filter(im,)    %第二个参数表示标准差

随着σ 的增加，一幅图像被模糊的程度。σ 越大，处理后的图像细节丢失越多。如果打算模糊一幅彩色图像，只需简单地对每一个颜色通道进行高斯模糊：

im = array(Image.open('empire.jpg'))
im2 = zeros(im.shape)
for i in range():
   im2[:,:,i] = filters.gaussian_filter(im[:,:,i],)
im2 = uint8(im2)

原始图像                                       使用σ=5的高斯滤波器

2.图像导数

在很多应用中图像强度的变化情况是非常重要的信息。强度的变化可以用灰度图像I（对于彩色图像，通常对每个颜色通道分别计算导数）的x和y 方向导数I_x 和I_y 进行描述。图像的梯度向量为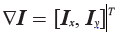。梯度有两个重要的属性，一是梯度的大小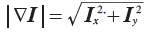：，它描述了图像强度变化的强弱，一是梯度的角度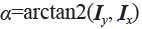：，描述了图像中在每个点（像素）上强度变化最大的方向。NumPy 中的arctan2() 函数返回弧度表示的有符号角度，角度的变化区间为-π...π。可以用离散近似的方式来计算图像的导数。图像导数大多数可以通过卷积简单地实现：。

对于Dx 和Dy，通常选择Prewitt 滤波器：

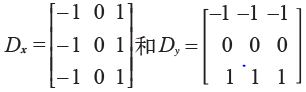
或者Sobel 滤波器：

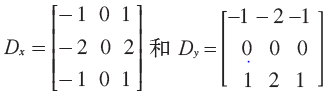
这些导数滤波器可以使用scipy.ndimage.filters 模块的标准卷积操作来简单地实现：

from PIL import Image
from numpy import *
from scipy.ndimage import filters
im = array(Image.open('empire.jpg').convert('L'))  #转化为灰度图像
# Sobel 导数滤波器
imx = zeros(im.shape)
filters.sobel(im,,imx)
imy = zeros(im.shape)
filters.sobel(im,,imy)
magnitude = sqrt(imx**+imy**)

上面的脚本使用Sobel 滤波器来计算x 和y 的方向导数，以及梯度大小。sobel() 函数的第二个参数表示选择x 或者y 方向导数，第三个参数保存输出的变量。在两个导数图像中，正导数显示为亮的像素，负导数显示为暗的像素。灰色区域表示导数的值接近于零。

上述计算图像导数的方法有一些缺陷：在该方法中，滤波器的尺度需要随着图像分辨率的变化而变化。为了在图像噪声方面更稳健，以及在任意尺度上计算导数，可以使用高斯导数滤波器：。

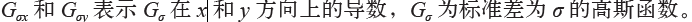
之前用于模糊的filters.gaussian_filter() 函数可以接受额外的参数，用来计算高斯导数。可以简单地按照下面的方式来处理：   

sigma =  # 标准差
imx = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (,), imx)
imy = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (,), imy)

该函数的第三个参数指定对每个方向计算哪种类型的导数，第二个参数为使用的标准差。