topcoder srm 485 div1

problem1 link

枚举第一个数和第二个数即可确定公差。

problem2 link

设高度为$n$,宽度为$m$，且$n \ge m$

如果$m \ge 5$，那么答案为0。这个可以通过抽屉原理来说明。考虑第一行，假设$n=m=5$，那么第一行最后一定有至少3个白色或黑色，不妨设为白色。不妨单独将这3列抽出来，现在就是一个$5*3(n=5)$的矩阵。那么对于第2，3，4，5行来说，不会存在一行有两个白色。对于黑色格子来说有两种情况：

（1）存在一行有三个黑色。那么其他三行不能有两个或者三个黑色，所以只能是一个黑色，这意味有两个白色，这样就和第一行冲突了。

（2）不存在任意一行有三个黑色，因为也不能有两个白色，所以只能是一个白色两个黑色，那么有三种排列方式，黑黑白，黑白黑，白黑黑。这样的话只能满足4行，第五行无论怎么放置都会冲突。如下图所示：

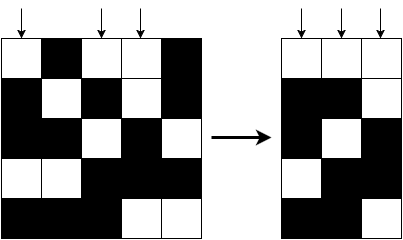
所以只需要考虑$m \le 4$的情况。

假设$m=4$，假设已经放置好了第1行到第$i-1$行，那么对于第$i$行来说，只需要记录一些信息来判断第$i$行的某两列是否可以都是白色或者都是黑色即可（保证不跟上面的某一行的两列形成不合法的情况）。

这样的话只有$C_{4}^{2}=6$种情况，即:0011,0101,1001,0110,1010,1100。将它们编号为0到5.

设dp的数组为$f[n][2^{6}][2^{6}]$

所以可以用一个状态$f[i][wst][bst]$来表示前$i$行放置之后，后面每一行不能出现白色格子的状态为$wst$且黑色格子状态为$bst$的放置方案数。

problem3 link

首先，对于凸包H上任意一点p,H上距离p最远的点一定是H的某个顶点。

其次，距离凸包上p附近的一些点的最远顶点必定跟距离p的最远顶点是同一个顶点。

所以，首先需要对H的边进行一些划分，也就是划分成若干个片段，每个片段的最远点是同一个顶点。划分的方法是枚举H的任意两个顶点$a,b$，线段$ab$的垂直平分线将H分为两半，一半的点到$a$的距离最大，另一半到$b$最大。该垂直平分线与H有两个交点。将所有的这样的交点收集在一起，那么任意两个相邻的交点所划分的一定是满足上面描述的一个片段。

然后就是对每个片段依次进行计算。设片段为$s$，距离$s$的最远点为$L$，其实就是计算假设$L$有一个光源，$s$上有多长的距离被内部凸包遮挡。可以这样计算：枚举内部凸包的每个点$p$，计算由$p,L$确定的直线与线段$s$的交点，那么对于任意两个$s$上的相邻交点$p_{1},p_{2}$,如果$p_{1},p_{2}$的中点与$L$组成的线段与内部凸包有交点，那么线段$p_{1}p_{2}$被遮挡。

code for problem1

import java.util.*;
import java.math.*;
import static java.lang.Math.*;

public class AfraidOfEven {

	final static int MAX = Integer.MAX_VALUE;
	public int[] restoreProgression(int[] seq) {
		final int n = seq.length;
		int[] result = new int[n];
		for (long a = 1; a * seq[0] <= MAX; a <<= 1) {
			for (long b = 1; b * seq[1] <= MAX; b <<= 1) {
				result[0] = (int)(seq[0] * a);
				result[1] = (int)(seq[1] * b);
				if (check(result, seq)) {
					return result;
				}
			}
		}
		return result;
	}
	boolean check(int[] a, int[] b) {
		int d = a[1] - a[0];
		for (int i = 2; i < b.length; ++ i) {
			long t = b[i];
			while (t <= MAX && t - a[i - 1] != d) {
				t <<= 1;
			}
			if (t > MAX) {
				return false;
			}
			a[i] = (int)t;
		}
		return true;
	}
}

　　

code for problem2

import java.util.*;
import java.math.*;
import static java.lang.Math.*;

public class RectangleAvoidingColoring {

	public long count(String[] board) {
		if (board.length >= 5 && board[0].length() >= 5) {
			return 0;
		}
		if (board[0].length() >= 5) {
			String[] board1 = new String[board[0].length()];
			for (int i = 0; i < board[0].length(); ++ i) {
				StringBuilder sb = new StringBuilder();
				for (int j = 0; j < board.length; ++ j) {
					sb.append(board[j].charAt(i));
				}
				board1[i] = sb.toString();
			}
			return count(board1);
		}
		final int n = board.length;
		final int m = board[0].length();

		if (m == 1) {
			long result = 1;
			for (int i = 0; i < n; ++ i) {
				if (board[i].charAt(0) == '?') {
					result <<= 1;
				}
			}
			return result;
		}

		final int K = m * (m - 1) / 2;

		int[] T1 = new int[1 << m];
		for (int i = 0, id = 0; i < (1 << m); ++ i) {
			int num = 0;
			for (int j = 0; j < m; ++ j) {
				if (contains(i, 1 << j)) {
					++ num;
				}
			}
			if (num == 2) {
				T1[i] = id ++;
			}
		}

		int[][] T = new int[1 << m][2];
		for (int i = 0; i < (1 << m); ++ i) {
			int b = 0;
			int w = 0;
			for (int x = 0; x < m; ++ x) {
				boolean bx = contains(i, 1 << x);
				for (int y = x + 1; y < m; ++ y) {
					boolean by = contains(i, 1 << y);
					if (bx != by) {
						continue;
					}
					if (by) {
						b |= 1 << T1[1 << x | 1 << y];
					}
					else {
						w |= 1 << T1[1 << x | 1 << y];
					}
				}
			}
			T[i][0] = w;
			T[i][1] = b;
		}

		long[][][] f = new long[n + 1][1 << K][1 << K];
		f[0][0][0] = 1;
		for (int i = 1; i <= n; ++ i) {
			for (int wst = 0; wst < (1 << K); ++ wst) {
				for (int bst = 0; bst < (1 << K); ++ bst) {
					final long val = f[i - 1][wst][bst];
					if (val == 0) {
						continue;
					}
					for (int st = 0; st < (1 << m); ++ st) {
						if (check(st, board[i - 1])) {
							int w = T[st][0];
							int b = T[st][1];
							if (contains(wst, w) || contains(bst, b)) {
								continue;
							}
							f[i][wst | w][bst | b] += val;
						}
					}
				}
			}
		}
		long result = 0;
		for (int wst = 0; wst < (1 << K); ++ wst) {
			for (int bst = 0; bst < (1 << K); ++bst) {
				result += f[n][wst][bst];
			}
		}
		return result;
	}

	static boolean contains(int st, int sub) {
		return (st & sub) != 0;
	}
	static boolean check(int st, String s) {
		for (int i = 0; i < s.length(); ++ i) {
			int t = (st >> i) & 1;
			if (t == 0 && s.charAt(i) == 'B'
					|| t == 1 && s.charAt(i) == 'W') {
				return false;
			}
		}
		return true;
	}
}

　　

code for problem3

import java.util.*;

public class Deposit {

	static final double EPS = 1e-9;

	static boolean isZero(double x) {
		return -EPS < x && x < EPS;
	}

	static class Point {
		double x;
		double y;

		Point() {}
		Point(double x, double y) {
			this.x = x;
			this.y = y;
		}

		double multiply(Point p) {
			return x * p.y - y * p.x;
		}
		Point multiply(double t) {
			return new Point(x * t, y * t);
		}
		Point divide(double t) {
			return new Point(x / t, y / t);
		}

		Point substract(Point p) {
			return new Point(x - p.x, y - p.y);
		}

		Point add(Point p) {
			return new Point(x + p.x, y + p.y);
		}

		Point vertical() {
			return new Point(-y, x);
		}

		double length() {
			return Math.sqrt(x * x + y * y);
		}

		boolean equals(Point p) {
			return isZero(x - p.x) && isZero(y - p.y);
		}

	}

	static class PointComparator implements Comparator<Point> {

		Point start;

		PointComparator(Point start) {
			this.start = start;
		}

		public int compare(Point o1, Point o2) {
			double d1 = o1.substract(start).length();
			double d2 = o2.substract(start).length();
			if (isZero(d1 - d2)) {
				return 0;
			}
			return d1 < d2? -1 : 1;
		}
	}

	Point[] out = null;
	Point[] inner = null;
	int n;
	int m;

	public double successProbability(int[] siteX, int[] siteY, int[] depositX, int[] depositY) {
		n = siteX.length;
		out = new Point[n];
		for (int i = 0; i < n; ++ i) {
			out[i] = new Point(siteX[i], siteY[i]);
		}
		m = depositX.length;
		inner= new Point[m];
		for (int i = 0; i < m; ++ i) {
			inner[i] = new Point(depositX[i], depositY[i]);
		}
		double sum = 0;
		for (int i = 0; i < n; ++ i) {
			sum += out[i].substract(out[(i + 1) % n]).length();
		}

		double validLength = 0;
		for (int i = 0; i < n; ++ i) {
			Point p = out[i];
			Point q = out[(i + 1) % n];
			validLength += calculate(p, q);
		}
		return validLength / sum;
	}

	double calculate(Point start, Point end) {

		List<Point> allRange = new ArrayList<>();
		allRange.add(start);
		allRange.add(end);
		for (int i = 0; i < n; ++ i) {
			for (int j = i + 1; j < n; ++ j) {
				Point p = out[i].add(out[j]).multiply(0.5);
				Point q = p.add(out[i].substract(out[j]).vertical());
				if (isParallel(start, end, p, q)) {
					continue;
				}
				Point c = getLineCrossLine(start, end, p, q);
				if (isOnSegment(c, start, end)) {
					allRange.add(c);
				}
			}
		}
		Collections.sort(allRange, new PointComparator(start));

		double result = 0;
		for (int i = 0; i + 1 < allRange.size(); ++ i) {
			Point a = allRange.get(i);
			Point b = allRange.get(i + 1);
			if (a.equals(b)) {
				continue;
			}
			Point f = getFarthestPoint(a.add(b).multiply(0.5), out);
			result += checkBlocked(a, b, f, inner);
		}
		return result;
	}

	static boolean isBetween(double a, double L, double R) {
		if (L < R) {
			return L - EPS < a && a < R + EPS;
		}
		return R - EPS < a && a < L + EPS;
	}

	static boolean isOnSegment(Point a, Point p, Point q) {
		return isBetween(a.x, p.x, q.x) && isBetween(a.y, p.y, q.y);
	}

	double checkBlocked(Point start, Point end, Point L, Point[] h) {
		List<Point> list = new ArrayList<>();
		list.add(start);
		list.add(end);
		for (Point hp: h) {
			if (isParallel(start, end, L, hp)) {
				continue;
			}
			Point p = getLineCrossLine(start, end, L, hp);
			if (isOnSegment(p, start, end)) {
				list.add(p);
			}
		}
		Collections.sort(list, new PointComparator(start));

		double result = 0;
		for (int i = 0; i + 1 < list.size(); ++ i) {
			Point p = list.get(i);
			Point q = list.get(i + 1);
			if (p.equals(q)) {
				continue;
			}
			if (isIntersectConvex(p.add(q).multiply(0.5), L, h)) {
				result += p.substract(q).length();
			}
		}
		return result;
	}

	static boolean isIntersectConvex(Point p, Point q, Point[] h) {
		for (int i = 0; i < h.length; ++ i) {
			Point a = h[i];
			Point b = h[(i + 1) % h.length];
			if (isParallel(a, b, p, q)) {
				continue;
			}
			Point c = getLineCrossLine(a, b, p, q);
			if (isOnSegment(c, p, q) && isOnSegment(c, a, b)) {
				return true;
			}
		}
		return false;
	}

	static boolean isParallel(Point a, Point b, Point p, Point q) {
		return isZero(a.substract(b).multiply(p.substract(q)));
	}

	static Point getFarthestPoint(Point p, Point[] h) {
		int id = 0;
		double dmax = 0;
		for (int i = 0; i < h.length; ++ i) {
			Point q = h[i];
			double d = p.substract(q).length();
			if (d > dmax) {
				id = i;
				dmax = d;
			}
		}
		return h[id];
	}

	static Point getLineCrossLine(Point a, Point b, Point p, Point q) {
		double s1 = p.substract(a).multiply(q.substract(a));
		double s2 = q.substract(b).multiply(p.substract(b));
		return a.multiply(s2).add(b.multiply(s1)).divide(s1 + s2);
	}
}