对于一张无边权的DAG图，给定n个起点和对应的n个终点，这n条不相交路径的方案数为

det(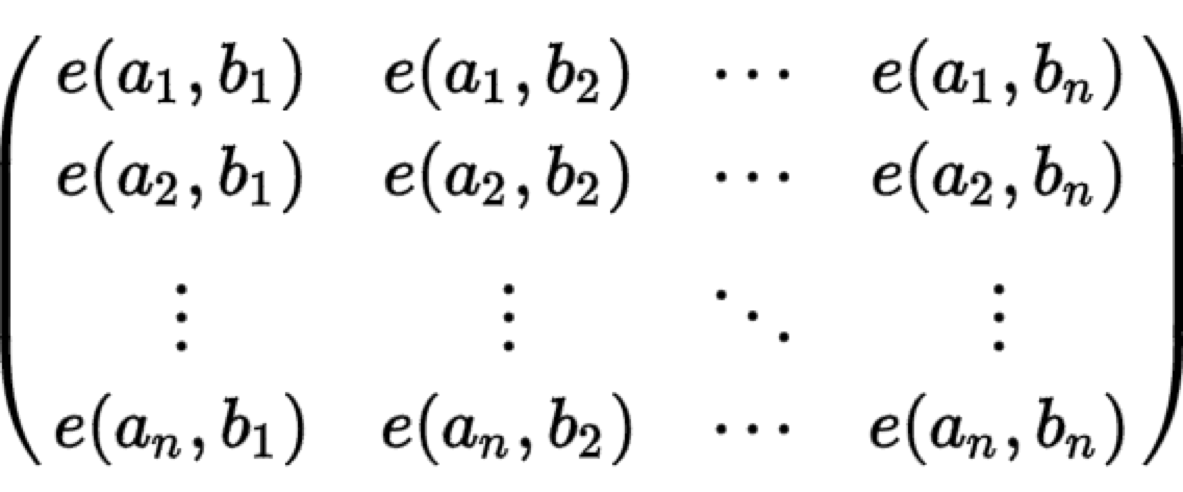) （该矩阵的行列式）

其中e(a,b)为图上a到b的方案数

codeforces 348D

[给定一张n*m带障碍的图，求从左上角到右下角不相交两条路径的方案]

[a1=(1,2) a2=(2,1) b1=(n-1,m) b2=(n,m-1) 应用该定理即可]

HDU 5852

[给一张n*n的图，第一行m个点对应第n行的m个点，求路径不相交的方案数]

[计算对应的行列式，注意高斯消元不要T]

[据说Q神想到是行列式之后在机房大喊一声，结果其他队伍都会做了，自己T了:D]

附录: 该定理wiki

Lindström–Gessel–Viennot lemma 应用两则的更多相关文章

  1. 牛客网多校训练第一场 A - Monotonic Matrix（Lindström–Gessel–Viennot lemma）

    链接: https://www.nowcoder.com/acm/contest/139/A 题意: 求满足以下条件的n*m矩阵A的数量模(1e9+7):A(i,j) ∈ {0,1,2}, 1≤i≤n ...

  2. Nowcoder Monotonic Matrix ( Lindström–Gessel–Viennot lemma 定理 )

    题目链接 题意 : 在一个 n * m 的矩阵中放置 {0, 1, 2} 这三个数字.要求 每个元素 A(i, j) <= A(i+1, j) && A(i, j) <= ...

  3. Lindström–Gessel–Viennot lemma定理 行列式板子

    https://blog.csdn.net/qq_37025443/article/details/86537261 博客 下面是wiki上的讲解,建议耐心地看一遍...虽然看了可能还是不懂 http ...

  4. Lindström–Gessel–Viennot lemma

    解决不相交路径计数 有两个大小为N的点集A,B A上每一个点对应着B的每一个点 求满足条件的路径集合有多少个 图里面可能还有一些障碍 Codeforces 348 D 有一个N*M的网格图 有两个点 ...

  5. LGV 算法 (Lindström–Gessel–Viennot lemma)

    e(ai,bi)为从起点ai到终点bi的方案数.以上矩阵行列式结果就是(a1,a2,...an) 到 (b1,b2,...bn) 的所有不相交路径的种数. 具体证明的话看wiki,比较长.. 这个定理 ...

  6. Codeforces 348 D - Turtles Lindström–Gessel–Viennot lemma

    #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second ...

  7. 排列组合( Lindström–Gessel–Viennot lemma 定理)

    链接:https://www.nowcoder.com/acm/contest/139/A来源:牛客网 Monotonic Matrix 时间限制:C/C++ 1秒,其他语言2秒空间限制:C/C++ ...

  8. 牛客网 暑期ACM多校训练营（第一场）A.Monotonic Matrix-矩阵转化为格子路径的非降路径计数，Lindström-Gessel-Viennot引理-组合数学

    牛客网暑期ACM多校训练营(第一场) A.Monotonic Matrix 这个题就是给你一个n*m的矩阵,往里面填{0,1,2}这三种数,要求是Ai,j⩽Ai+1,j,Ai,j⩽Ai,j+1 ,问你 ...

  9. Codeforces.348D.Turtles(容斥 LGV定理 DP)

    题目链接 \(Description\) 给定\(n*m\)的网格,有些格子不能走.求有多少种从\((1,1)\)走到\((n,m)\)的两条不相交路径. \(n,m\leq 3000\). \(So ...

随机推荐

  1. Codeforces Round #462 (Div. 2) C. A Twisty Movement

    C. A Twisty Movement time limit per test1 second memory limit per test256 megabytes Problem Descript ...

  2. python之随机数random模块

    random模块:用于生成随机数 import random #random模块:用于生成随机数 li = [] for i in range(7): r = random.randrange(0,3 ...

  3. Flask 中蓝图的两种表现形式

    最近在学Flask,特有的@X.route 很适合RESTfuld API, 一般小型应用,在一个py文件中就可以完成,但是维护起来比较麻烦. 想体验Django那样的MVT模式, 看到 Flask提 ...

  4. 【Next Permutation】cpp

    题目: Implement next permutation, which rearranges numbers into the lexicographically next greater per ...

  5. C++文件读写之对象的读写

    这里以一个简单的学生信息管理系统为例. 首先是对象的建立,包括姓名,学号,成绩,学分,等 如下: 这里面包括两个子对象, class Student { public: Student() :scor ...

  6. 踩坑 Uncaught RangeError: Maximum call stack size exceeded

    今天遇到了一个错误, 堆栈溢出,很好奇就是一个简单ajax请求怎么会报这个错误,研究了一下,发现犯了一个很低级的错误,data的参数错误了: passWord是未定义的变量,值为空,然后导致了这个问题 ...

  7. 练习题 - js函数

    代码贴出来 1 function Cat() { 2 getColor = function(){ console.log(1);} 3 return this; 4 } 5 Cat.getColor ...

  8. Git详解之二 Git基础 转

    http://www.open-open.com/lib/view/open1328069733264.html Git 基础 读完本章你就能上手使用 Git 了.本章将介绍几个最基本的,也是最常用的 ...

  9. NSByteCountFormatter

    可以将字节转化为我们需要的Kb或者m + (NSString *)stringFromByteCount:(long long)byteCount countStyle:(NSByteCountFor ...

  10. 使用CoreLocation进行定位（Swift版）

    在应用开发中,很多情况需要我们获取到当前的位置和高度信息,方便搜索周边,查看周边相同应用等,一切与定位有关的都得使用CoreLocation库,而且,系统是不允许第三发定位的,当然可以使用第三方对其封 ...