ACM/ICPC 之 数论-斐波拉契●卢卡斯数列(HNNUOJ 11589)

　　

---

　　看到这个标题，貌似很高大上的样子= =，其实这个也是大家熟悉的东西，先给大家科普一下斐波拉契数列。

• 斐波拉契数列

　　　　又称黄金分割数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……

　　　　在数学上，斐波纳契数列以如下被以递归的方法定义：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*）

　　　　在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

• 斐波拉契数列与黄金分割-----(涉及今天的例题)

　　　　有趣的是：这样一个完全是自然数的数列，通项公式却是用无理数来表达的。而且当n趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割0.618.（或者说后一项与前一项的比值小数部分越来越逼近黄金分割0.618、前一项与后一项的比值越来越逼近黄金分割0.618）

　　　　1÷1=1，1÷2=0.5，2÷3=0.666...，3÷5=0.6，5÷8=0.625，…………，55÷89=0.617977…，…………144÷233=0.618025…46368÷75025=0.6180339886…...

　　　　越到后面，这些比值越接近黄金比.

 

• 斐波拉契数列-部分数学规律

　　　　　　　　　　偶数项求和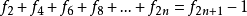

 

　　　　　　　　　　平方求和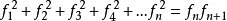

 

 

---

 

　　以下正式入题啦~

• 斐波拉契-卢卡斯数列

　　　　卢卡斯数列1、3、4、7、11、18…，也具有斐波那契数列同样的性质。（我们可称之为斐波那契—卢卡斯递推：从第三项开始，每一项都等于前两项之和f(n) = f(n-1)+ f(n-2）。

　　　　这两个数列还有一种特殊的联系（如下表所示），F（n）*L（n）=F(2n），及L（n）=F（n-1)+F(n+1)

n	1	2	3	4	5	6	7	8	9	10	…
斐波那契数列F(n)	1	1	2	3	5	8	13	21	34	55	…
卢卡斯数列L(n)	1	3	4	7	11	18	29	47	76	123	…
F(n)*L(n)	1	3	8	21	55	144	377	987	2584	6765	…

　　　　类似的数列还有无限多个，我们称之为斐波那契—卢卡斯数列。

　　　　如1，4，5，9，14，23…，因为1，4开头，可记作F[1，4]，斐波那契数列就是F[1，1]，卢卡斯数列就是F[1，3]，斐波那契—卢卡斯数列就是F[a，b]。

　　　　

• 与斐波拉契数列的另一个共同性质：　　
• 中间项的平方数与前后两项之积的差的绝对值是一个恒值

　　　　斐波那契数列：|1*1-1*2|=|2*2-1*3|=|3*3-2*5|=|5*5-3*8|=|8*8-5*13|=…=1

　　　　卢卡斯数列：|3*3-1*4|=|4*4-3*7|=…=5

　　　　F[1，4]数列：|4*4-1*5|=11

　　　　F[2，5]数列：|5*5-2*7|=11

　　　　F[2，7]数列：|7*7-2*9|=31

• 黄金特征-----（与例题有关）

　　　　斐波那契数列这个值是1最小，也就是前后项之比接近黄金比例最快，我们称为黄金特征

　　　　黄金特征1的数列只有斐波那契数列，是独生数列。卢卡斯数列的黄金特征是5，也是独生数列。

　　　　前两项互质的独生数列只有斐波那契数列和卢卡斯数列这两个数列。

 

---

 

　　应用例题：

　　　　

 

　　　　

　　　　题意：大致就是给定一个斐波拉契-卢卡斯数列中的某一项a_n（题目没有说明，但是这其实就是斐波拉契卢卡斯数列），然后让你求出初始的斐波拉契-卢卡斯数列a₁和a₂的值，并使得a₂尽可能小。

 

　　　　我用的是数学规律的思路

• 在一个斐波拉契-卢卡斯数列的无穷大项(记为第m项)，则第m-1项除以m项一定无限接近黄金分割0.618---可以计算倒数第二项的模糊值(设为a)
• 且m足够大时，(m-1)/m>=0.618
• 需要注意：在m值较大时，(m-1)/m即便很接近0.618，但m值太大，因此0.618*m得到的模糊值也会有较大误差，所以需要a++直到找到最适合的前两项
• 上一点注意的详细公式是：小于两倍的sqrt(n)。

 //斐波拉契-卢卡斯数列
 //Memory 1100 K,Time: 234 Ms
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;

 #define INF 0x3f3f3f3f

 int m1,m2;    //让第二项最小的初始两项

 //计算初始两项并刷新最适合的m1，m2
 void compute(int a,int b,int t)
 {
     while(t <= a && t >= )
     {
         b = a;
         a = t;
         t = b - a;
     }
     if(m2 > b)
     {
         m1 = a;
         m2 = b;
     }
 }

 int main()
 {
     int T,n;
     scanf("%d",&T);

     while(T--)
     {
         int a,t;
         scanf("%d",&n);
         a = (int)(0.618*n)-;    //倒数第二项模糊值

         m1 = m2 = INF;
         int i = -;
         while(a+(++i) <= n && i <= (int)*sqrt(n))    //倒数第二项小于最后一项，且次数小于2*sqrt(n)
         {
             compute(a+i,n,n-a-i);
         }

         printf("%d %d\n",m1,m2);
     }

     return ;
 }

　　上述Code的 i <= (int)2*sqrt(n)的不等式是小编试出来的，测试数据在这些次数内可以过，如果不加的话，肯定是TLE的。

　　大家如果有更加合适的Code可以写在评论里面(⊙o⊙)哦~，小编太渣了，没有更加清楚明白的思路= =

　　Fighting~

---