P1033 自由落体

原题链接 https://www.luogu.org/problemnew/show/P1033

不得不说，这个题太坑了！！！主要是题目说得不明确......

先来看图：

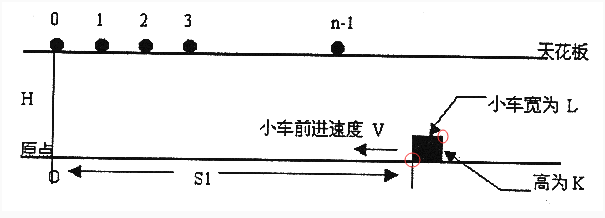
看一下用红圈圈起来的部分，就是说小车运动过程中如果有一个小球在小车的正前方（与小车的距离在0.0001m以内）且这个小球的高度在0～ch（车高），则可以接到这个球（很神奇吧，没被撞飞）

还有就是如果有一个小球在小车的后方（与小车的距离在0.0001m以内）且这个小球的高度为ch，则也可以接到这个球

这样看来，就引出了我的思路：

用for循环从0～n-1来判断当车运动过程中小球是否在车的左下角和右上角的范围内，在的话ans++

那么怎么求是否在车的左下角呢

小球落到左下角的高度为qh（球本来的高度），那么所需时间为t=sqrt(qh/5)，小车与原点的距离为s-sqrt(qh/5)*cv(车速)，所以小球i只要>=s-sqrt(qh/5)*cv-0.0001就能接到

当然也要在小车的右上角范围内： 这时小球落到左上角（与右上角一样）的高度为qh-ch，那么所需时间为t=sqrt((qh-ch)/5)，小车左上角与原点的距离为s-sqrt((qh-ch)/5)*cv，小车右上角与原点的距离为s-sqrt((qh-ch)/5)*cv+ck，所以小球i也要<=s-sqrt((qh-ch)/5)*cv+ck+0.0001

下面给出代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
int main()
{
double qh,ch,ck,cv,s;
int n,sum=;
scanf("%lf%lf%lf%lf%lf%d",&qh,&s,&cv,&ck,&ch,&n);
for(int i=;i<n;i++)
{
if(i>=s-sqrt(qh/)*cv-0.0001&&i<=s-sqrt((qh-ch)/)*cv+ck+0.0001) sum++;              //核心代码，算出小球是否在车的左下角和右上角的范围内
}
cout<<sum;
return ;
}