numpy中的广播

广播的引出 numpy两个数组的相加、相减以及相乘都是对应元素之间的操作。

import numpy as np

x = np.array([[2,2,3],[1,2,3]])

y = np.array([[1,1,3],[2,2,4]])

print(x*y)  #numpy当中的数组相乘是对应元素的乘积，与线性代数当中的矩阵相乘不一样

输入结果如下：

'''

[[ 2  2  9]

 [ 2  4 12]]

'''

当两个数组的形状并不相同的时候，我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播（broadcasting）。

比如，一个二维数组减去列平均值，来对数组的每一列进行距平化处理：

import numpy as np

arr = np.random.randn(4,3)  #shape(4,3)

arr_mean = arr.mean(0)      #shape(3,)

demeaned = arr -arr_mean

很明显上式arr和arr_mean维度并不形同，但是它们可以进行相减操作，这就是通过广播机制来实现的。

广播的原则

广播的原则：如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失和（或）长度为1的维度上进行。

这句话乃是理解广播的核心。广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为1。

数组维度不同，后缘维度的轴长相符

我们来看一个例子：

import numpy as np

arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]])  #arr1.shape = (4,3)

arr2 = np.array([1, 2, 3])    #arr2.shape = (3,)

arr_sum = arr1 + arr2

print(arr_sum)

输入结果如下:

'''

[[1 2 3]

 [2 3 4]

[3 4 5]

[4 5 6]]

'''

上例中arr1的shape为（4,3），arr2的shape为（3，）。可以说前者是二维的，而后者是一维的。但是它们的后缘维度相等，arr1的第二维长度为3，和arr2的维度相同。arr1和arr2的shape并不一样，但是它们可以执行相加操作，这就是通过广播完成的，在这个例子当中是将arr2沿着0轴进行扩展。

上面程序当中的广播如下图所示：

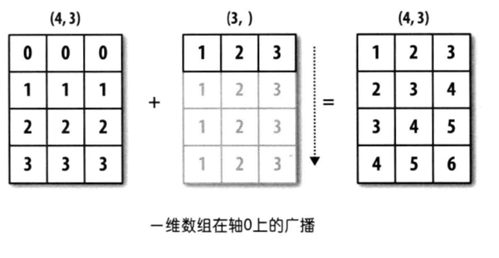
同样的例子还有：

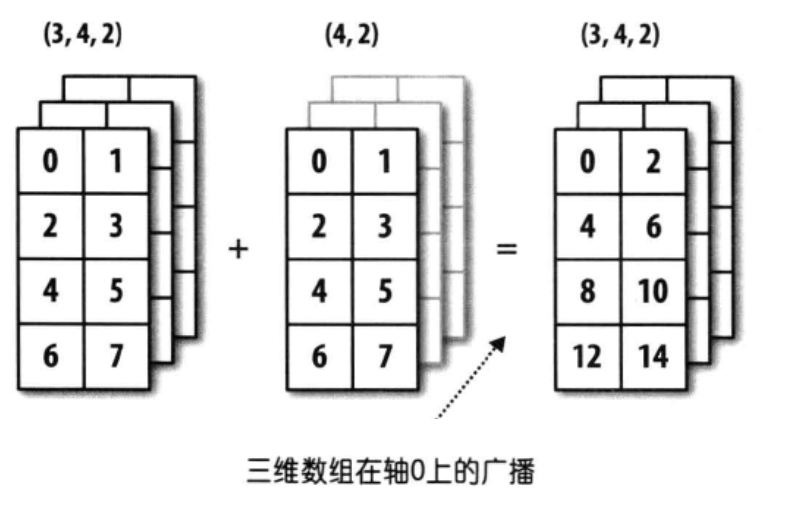
从上面的图可以看到，（3,4,2）和（4,2）的维度是不相同的，前者为3维，后者为2维。但是它们后缘维度的轴长相同，都为（4,2），所以可以沿着0轴进行广播。

同样，还有一些例子：（4,2,3）和（2,3）是兼容的，（4,2,3）还和（3）是兼容的，后者需要在两个轴上面进行扩展。

数组维度相同，其中有个轴为1

我们来看下面的例子：

import numpy as np

arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]])  #arr1.shape = (4,3)

arr2 = np.array([[1],[2],[3],[4]])    #arr2.shape = (4, 1)

arr_sum = arr1 + arr2

print(arr_sum)

输出结果如下：

[[1 1 1]

 [3 3 3]

 [5 5 5]

 [7 7 7]]

　　arr1的shape为（4,3），arr2的shape为（4,1），它们都是二维的，但是第二个数组在1轴上的长度为1，所以，可以在1轴上面进行广播，如下图所示：

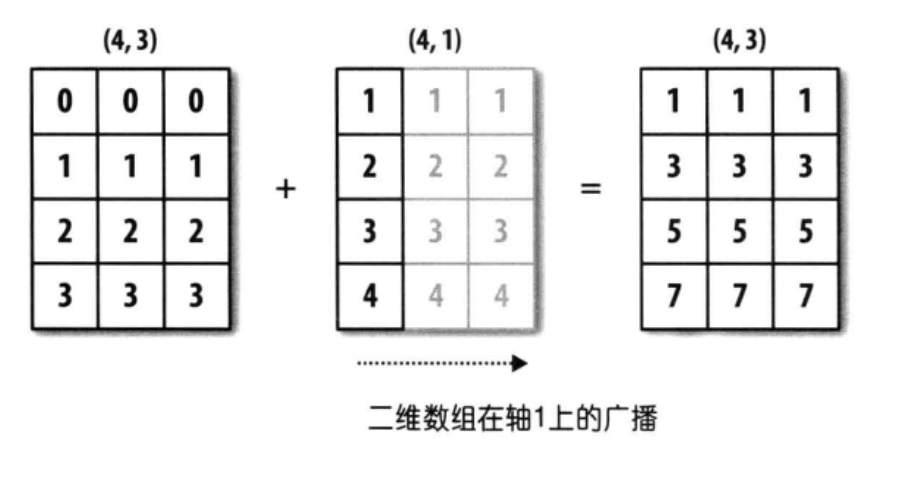
在这种情况下，两个数组的维度要保证相等，其中有一个轴的长度为1，这样就会沿着长度为1的轴进行扩展。这样的例子还有：（4,6）和（1,6）。（3,5,6）和（1,5,6）、（3,1,6）、（3,5,1），后面三个分别会沿着0轴，1轴，2轴进行广播。

后话：还有上面两种结合的情况，如（3,5,6）和（1,6）是可以相加的。在TensorFlow当中计算张量的时候也是用广播机制，并且和numpy的广播机制是一样的。

参考:

《利用python进行数据分析》第十一章广播本书的图片和广播的原则的描述都来自本书

看完这篇文章后，下面这篇文章的中的疑问也就迎刃而解了。

https://www.cnblogs.com/yangmang/p/7125458.html

numpy数组的广播功能强大，但是也同时让人疑惑不解，现在让我们来谈谈其中的原理。

广播原则：

如果两个数组的后缘维度(即：从末尾开始算起的维度)的轴长相符或其中一方的长度为1，则认为它们是广播兼容的，广播会在缺失和(或)长度为1的轴上进行.

上面的原则很重要，是广播的指导思想，下面我们来看看例子。

1.其实在最简单的数组与标量数字之间的运算就存在广播，只是我们把它看作理所当然了。

2.再看下一个例子，这个大家都会一致认为这是广播了

根据广播原则：arr1的shape为(4,1),arr2的shape为(3,),所以会同时在两个轴发生广播，arr1的shape变成(4，3)，而arr2的shape变成(4,3),所以结果也为(4,3).

其实代码中发生了下图描述的事情：

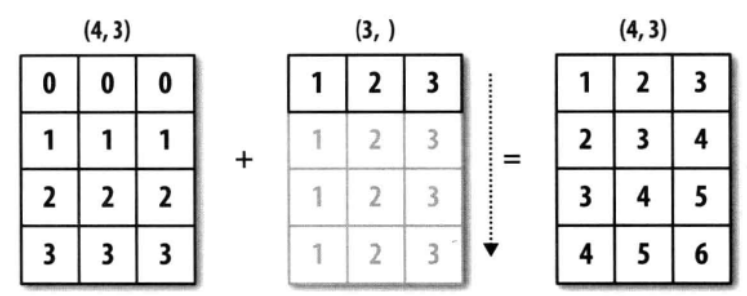
3.同理，我们可以得到三维数组的广播情况

根据广播原则分析：arr1的shape为(3,4,2),arr2的shape为(4,2)，它们的后缘轴长度都为(4,2)，所以可以在0轴进行广播，arr2的shape变为(3,4,2).

下面说明一下三维数组在各维度的广播形状需求：

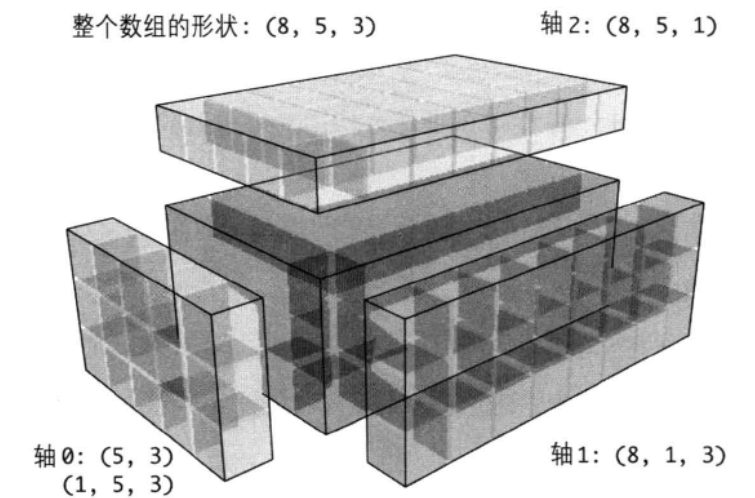
以上所有形状都可以发生广播，你可以用我们开篇所说的广播原则进行验证。

最后，再来说一个易错的实际例子。

arr减去他在1轴上的平均值，会出错？看看为啥。

因为arr.mean(1)产生的shape为(4,)，根据广播原则，较小的数组的后缘维度必须为1，

所以需要将arr.mean变成(4,1)，你所期望的结果如下：