NEO GUI 多方签名使用

众所周至，NEOGUI是一个开发者演示用钱包，使用体验是非常的不友好的。

今天本来打算使用多方签名账户，发现和想象的不一样，请教了小伙伴也不行。遂调试了一下原因，发现踩进坑里了。

 

 

把这个问题记录一下，希望以后用到的小伙伴可以顺利实施

准备阶段

首先准备两个key

Key1地址 ALjSnMZidJqd18iQaoCgFun6iqWRm2cVtj

Key1公钥 02aa792c61ffe03d92bb505969fe81e2c345682a9c0ba38596275f3a31f6da6e5f

Key2地址 AcfWad6TSjQbfrjyhkTuEPDRrYWYQC9zHD

Key2公钥 02a763b5d3bf02cbb4d7e03eb9b060021324d6074bcff046d9846fe3ae1cdc5031

我是不会给你私钥的，此处你应该准备自己的Key1、key2

 

为了测试的纯洁，新建一个钱包，随钱包生成的地址删了，不要了

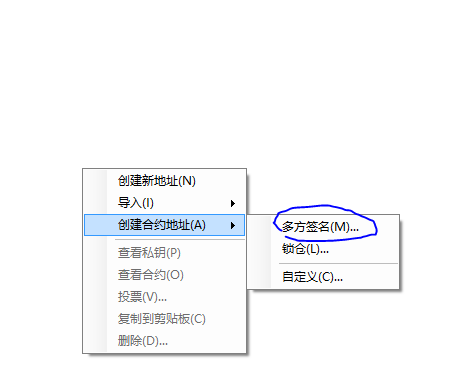
新建多方签名

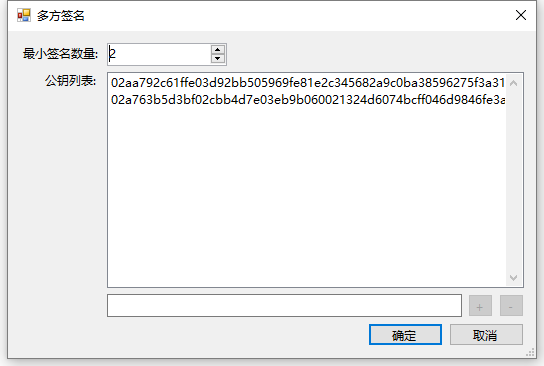
把key1公钥和key2公钥填进去，设置最小签名数量2.

意味着我们创建一个这两个地址都要签名的多方签名。

 

然后往这个多方签名地址里转点钱，这个都很顺利。

如果转账后、同步后多方签名地址里不能顺利显示余额，那你就

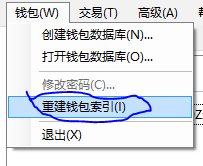
重建一下索引

 

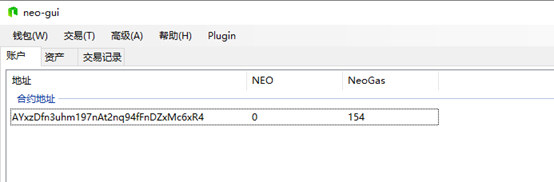
好了，我们给这个多方签名地址里面转入154gas，现在还没有什么问题

 

转出

然后，问题就来了

怎么从这个合约地址里面转账出来

转账

首先

转到一个地址15个GAS

 

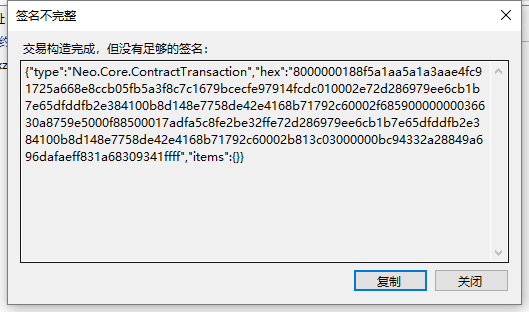
此时就会得到一个交易构造，但没有签名的对话框。很好，此时正常。

 

然后只要把这串东西发给一个key的拥有者签名

然后签名之后再发给另一个key的拥有者签名并广播

15个gas就可以取出来了。

理论如此，但有一些小坑

Key1拥有者

我们假定key1的拥有者准备签名了，那么key1的拥有者是不是可能为这个需求新建一个钱包呢，很可能，新建一个钱包，导入key1，执行签名。

好，我们来试一试。

 

Key1拥有者新建钱包，导入key1

然后签名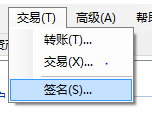你会得到

第一次失败

 

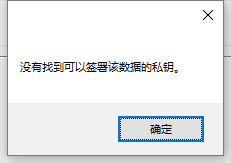
这是因为根据

这串东西，找不到和key1的关系

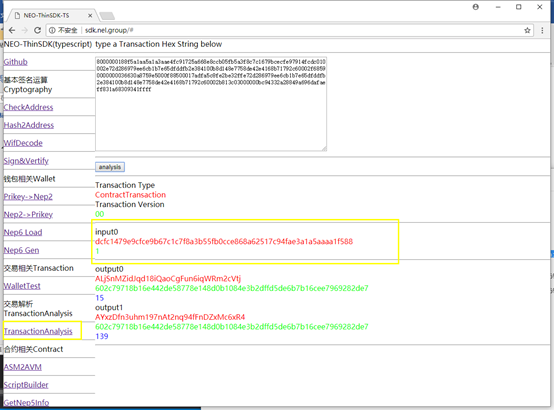
我们可以分析一下他生成的交易，这个交易有一个输入

交易的输入是一个UTXO

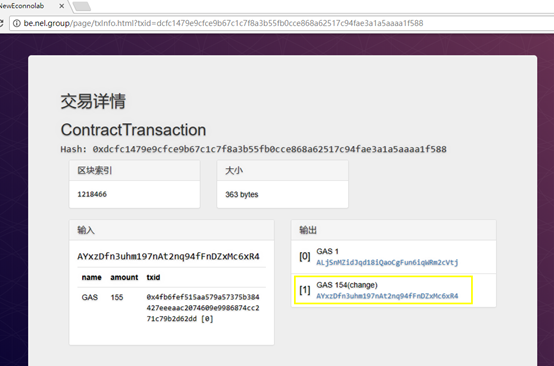
他指向的地址是Ayx……xR4,就是多方签名合约

所以，其实是需要多方签名合约来提供鉴证信息的。

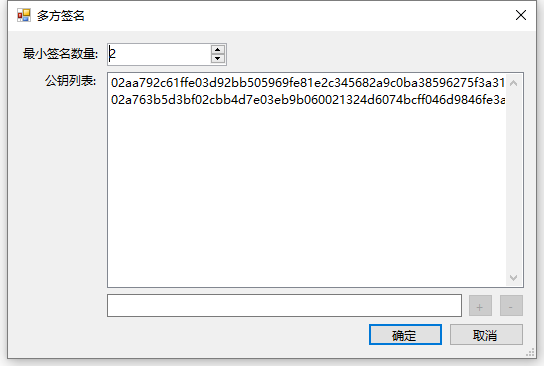
好，新建多方签名

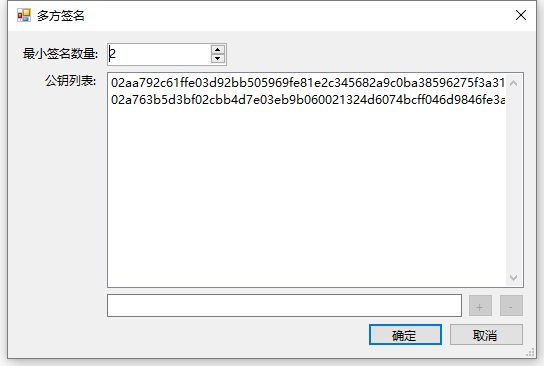
再执行一次签名，你会成功

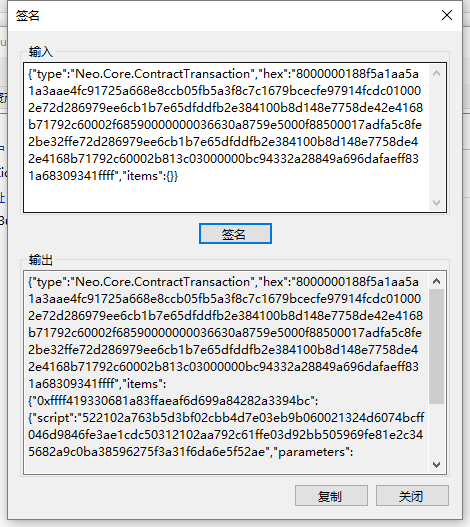
然后我们把输出的这串东西交给Key2拥有者

Key2拥有者

我们假定key2的拥有者准备签名了，key2的拥有者思路不太一样，他也为了清晰新建了一个钱包，然后先创建了多方签名合约，再导入了Key2，然后签名

 

第二次失败

然后key2拥有者会得到这个问题，明明有多方签名地址，也有key2，为什么还会没有这个信息呢。

 

这个地方就要解释一下源码了。观察了多方签名创建的代码

 

他是这个样子的，具体的关系就是。

 

多方签名合约对话框从多个签名中找一个key，只有我钱包里面能找到一个key，才能返回。

那就要求了创建多方签名合约时，你要想让这个钱包能用来签名，它里面必须有一个多方签名里面用到的key，而且只能有一个

因为你有两个Key，创建多方签名也只能关联一个key，而且很难判断关联的到底是哪个。

 

 

第二次失败的原因明确了

再来一次

必须先导入key2，再创建多方签名地址

修改后正常

点广播，钱取走

总结一下

使用NEOGUI操作多方签名合约。

需要注意

1.一个钱包里的多方签名合约只能关联一个KEY，如果没有KEY，他就不能用来签名。

也就是说如果你需要三个签名，你就需要三个钱包。

2.只有当前钱包中有KEY的情况下创建多方签名合约才会关联上。

 

产生转账交易

需要多方签名合约，无需关联KEY

签名1

需要多方签名合约，KEY1，多方签名合约必须关联KEY1

签名2

需要多方签名合约，KEY2，多方签名合约必须关联KEY2