Codeforces Round #550 (Div. 3) F. Graph Without Long Directed Paths

 

 

 

 

F. Graph Without Long Directed Paths

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a connected undirected graph consisting of nn vertices and mm edges. There are no self-loops or multiple edges in the given graph.

You have to direct its edges in such a way that the obtained directed graph does not contain any paths of length two or greater (where the length of path is denoted as the number of traversed edges).

Input

The first line contains two integer numbers nn and mm (2≤n≤2⋅1052≤n≤2⋅105, n−1≤m≤2⋅105n−1≤m≤2⋅105) — the number of vertices and edges, respectively.

The following mm lines contain edges: edge ii is given as a pair of vertices uiui, vivi (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi). There are no multiple edges in the given graph, i. e. for each pair (ui,viui,vi) there are no other pairs (ui,viui,vi) and (vi,uivi,ui) in the list of edges. It is also guaranteed that the given graph is connected (there is a path between any pair of vertex in the given graph).

Output

If it is impossible to direct edges of the given graph in such a way that the obtained directed graph does not contain paths of length at least two, print "NO" in the first line.

Otherwise print "YES" in the first line, and then print any suitable orientation of edges: a binary string (the string consisting only of '0' and '1') of length mm. The ii-th element of this string should be '0' if the ii-th edge of the graph should be directed from uiui to vivi, and '1' otherwise. Edges are numbered in the order they are given in the input.

Example

input

Copy

6 5
1 5
2 1
1 4
3 1
6 1

output

Copy

YES
10100

这个题的题意就是修改一些边的方向让有向图不包含长度为2或更大的任何路径（其中路径长度表示为遍历边的数量），修改的边标记为1，没修改的标记为0，最后按顺序输出所有的边的标记

如下图

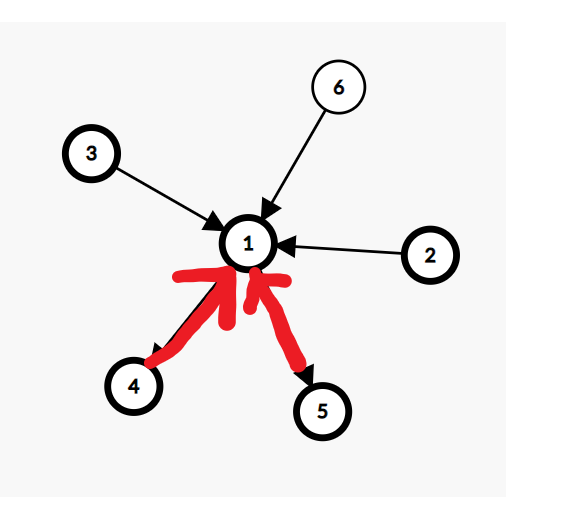
思路在下面代码的注释中

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
using namespace std;
const int maxn=2e5+;
const int inf=0x3f3f3f3f;
int n,m;
int first[maxn],sign;
int vis[maxn];
int a[maxn][];
struct node
{
    int to,w,next;
} edge[maxn<<];
void init()
{
    for(int i = ; i <=n; i++)
        first[i]=-;
    sign=;
}
void add_edge(int u,int v,int w)
{
    edge[sign].to=v;
    edge[sign].w=w;
    edge[sign].next=first[u];
    first[u]=sign++;
}
bool flag1=;
void dfs(int x,int flag)///对整个图进行染色1 0 1 0...，
{
    vis[x]=flag;
    for(int i=first[x]; ~i; i=edge[i].next)
    {
        int to=edge[i].to;
        if(vis[to]==vis[x])///判断是是否有环
        {
            flag1=;
            return ;
        }
        if(vis[to]==-)
        {
            dfs(to,flag^);
        }
    }
    return ;

}
int main()
{
    scanf("%d%d",&n,&m);
    init();
    for(int i=; i<=m; i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        add_edge(u,v,);
        add_edge(v,u,);
        a[i][]=u;
        a[i][]=v;
    }
    memset(vis,-,sizeof(vis));
    dfs(,);
    if(flag1)
        puts("NO");///如果图中有环的话，肯定就会存在dist>=2的点，可以自己画一个三角形看看，就很容易理解了
    else
    {
        puts("YES");
        for(int i=; i<=m; i++)
        {
            if(vis[a[i][]]==)///a[i][0]为第i条边的起点，a[i][1]为第i条边的终点。
                              ///这里我们已经将整个图染色，整个图分为两类，标记为1的点和标记为0的点
                              ///以标记为1的点为起点，出发的边不做修改，即边的标记为0
                              ///以标记为0的点为起点，出发的边改为相反的方向，即边的标记为1，
                              ///这里其实是不难理解的，两个相邻的点必定为1 0或者0 1，1->0->1
                              ///（1出发的边保持原来的方向，0出发的边改为相反的方向）或者（0出发
                              ///的边保持原来的方向，1出发的边改为相反的方向）才能使得整个图的不出现长度为2或者更大的路径
                printf("");
            else
                printf("");
        }
    }

    return ;
}