主成分分析算法(PCA)

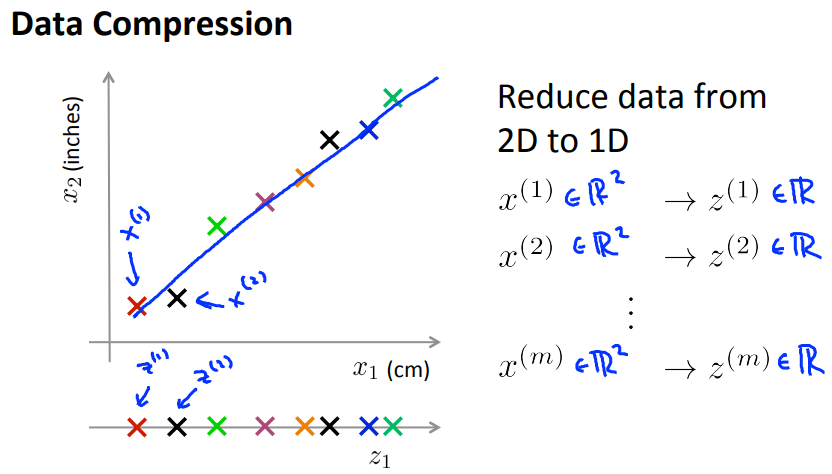
通过数据压缩（降维）可以减少特征数量，可以降低硬盘和内存的存储，加快算法的训练。

还可以把高维的数据压缩成二维或三维，这样方便做数据可视化。

数据压缩是通过相似或者相关度很高的特征来生成新的特征，减少特征数量。例如，上图x1是厘米，x2是英寸，这两个特征相关度很高，可以压缩成一个特征。

======================================

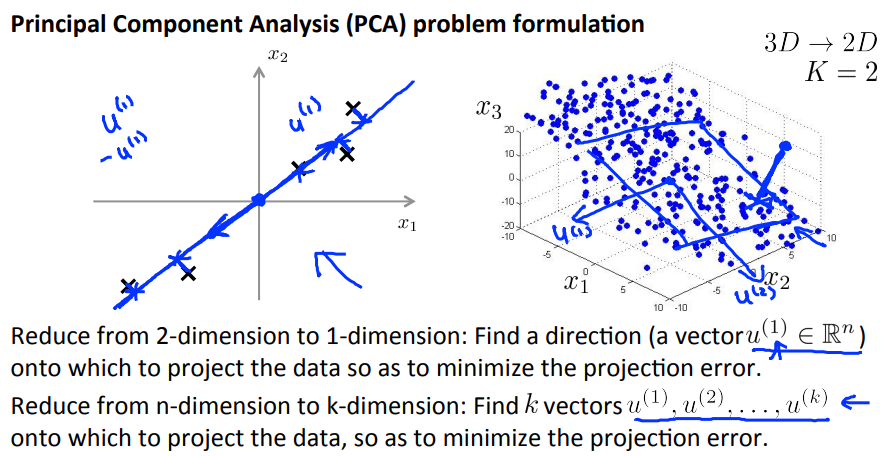
主成分分析（Principal Component Analysis, PCA）是常用的降维算法。

例如，要将二维数据压缩成一维数据，需要找到一个向量，使所有样本到该向量的投影误差（projection error）最小。

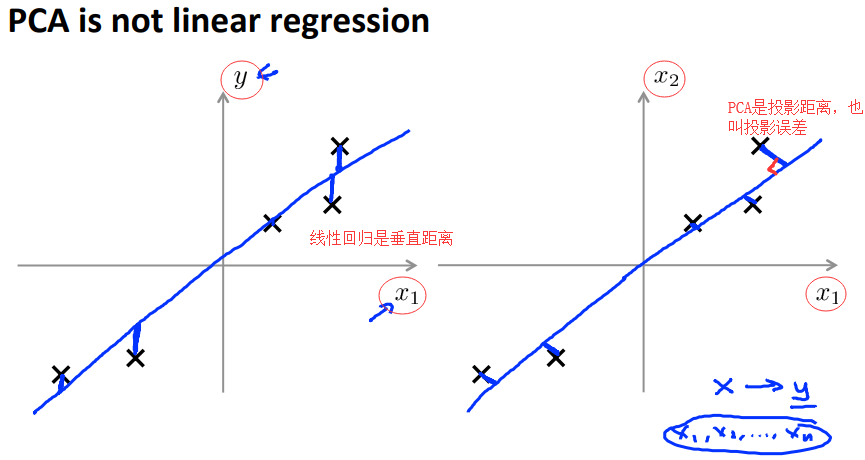
PCA不是线性回归，线性回归的差值是预测值和实际值的差，PCA的差值是样本到向量的投影误差。

线性回归需要用到标签，而PCA不需要用到标签。

======================================

在使用PCA算法前需要对数据进行预处理（每一个特征的均值要为0）。

首先需要计算协方差矩阵: sigma = (1/m) * X' * X

然后需要计算sigma的特征向量。 svd函数是奇异值分解（相关连接：https://www.cnblogs.com/pinard/p/6251584.html）

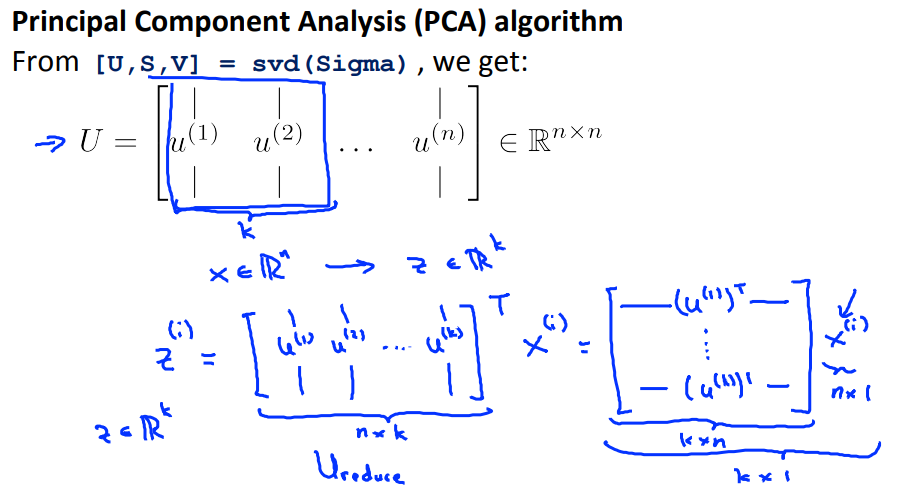
注意：每个特征的均值要为0，特征缩放是可选的。

svd返回的U是nxn维矩阵，前k列的矩阵称为Ureduce(nxk)。

Zi = Ureduce' * Xi

======================================

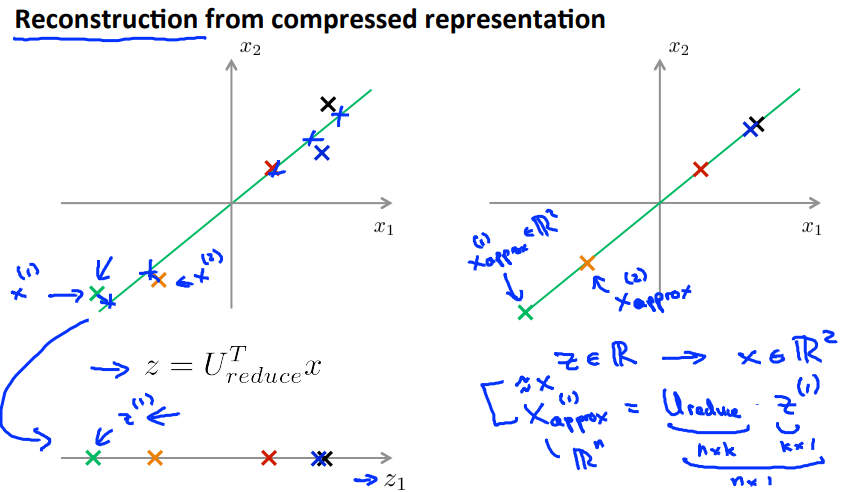
如何把压缩数据解压缩还原到原来的维度？

X(i)approx = Ureduce * Z(i)

======================================

如何选择合适的k值？即特征应该从n维降低到哪个维度？

1 - 投影误差的均方 / 总偏差  = 保留的样本差异（?% of variance is retained）

通常均方投影误差除以总偏差不大于0.01,0.05或0.10

在向别人描述降维结果的时候不是说从n维降低到了k维，而是说保留了多少百分比的样本差异。

======================================

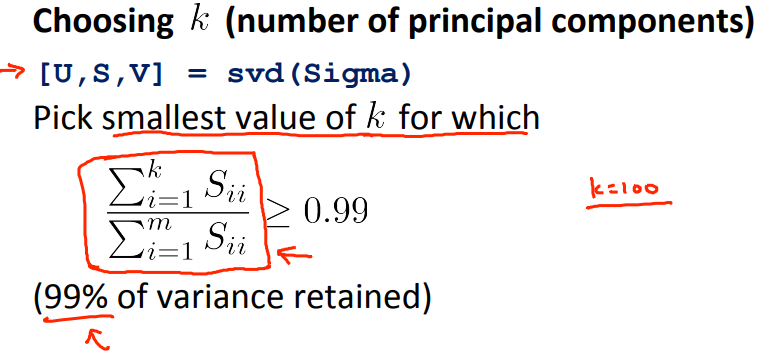
注意：PCA不适合用于处理过拟合。