XGBoost原理和公式推导

本篇文章主要介绍下Xgboost算法的原理和公式推导。关于XGB的一些应用场景在此就不赘述了，感兴趣的同学可以自行google。下面开始：

1.模型构建

构建最优模型的方法一般是最小化训练数据的损失函数，用L表示Loss Function（），F是假设空间：

\[
L = min_{f \in F} \ \frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) \quad \text{(1)}
\]
上述（1）式就是俗称的经验风险最小化，当训练数据集较小时，很容易过拟合，所以一般需要加入正则项来降低模型的复杂度。
\[
L = min_{f \in F} \ \frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i))+\lambda J(f) \quad \text{(2)}
\]
其中的J(f)为控制模型复杂度，式（2）称为结构风险最小化。
决策树的生成和剪枝分别对应了经验风险最小化和结构风险最小化。XGB决策树在生成过程中，即是结构风险最小化的结果。

2.Boosting算法介绍

对于Boosting算法我们知道，是将多个弱分类器的结果结合起来作为最终的结果来进行输出。对于回归问题，假设
\[f_{}^{t}(x_i) \]为第t棵树的输出结果，\[\hat{y}_{i}^{(t)} \]是模型当前的输出结果，\[y_{i}\]是实际的结果。
那么
\[
\hat{y}_{i}^{(t)} = \sum_{t=1}^{t}f^{t}(x_i) \quad \text{(3)}
\]
\[
\hat{y}_{i}^{(t)} = \hat{y}_{i}^{(t-1)}+f^{t}(x_i)\quad \text{(4)}
\]

3.XGBoost目标函数

通过最小化损失函数来构建最优模型，因此：
\[
obj(t) = \sum_{i=1}^nl(y_i,\hat{y}_{i})+\Omega(f(t)) + Constant\quad \text{(5)}
\]
等式右边第一部分是训练误差，中间是惩罚模型的复杂度（所有树的复杂度之和）该项中包含了两个部分，一个是叶子结点的总数，一个是叶子结点得到的L2正则化项。这个额外的正则化项能够平滑每个叶节点的学习权重来避免过拟合。直观地，正则化的目标将倾向于选择采用简单的模型。当正则化参数为零时，这个函数就变为传统的GBDT。
这里（5）结合（4）再进行泰勒展开，
\[
obj(t) \simeq \sum_{i=1}^n[l(y_i,\hat{y}^{t-1})+g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+ \Omega(f(t)) + Constant \quad \text{(6)}
\]
\[
g_i=\partial_{\hat{y}^{t-1}}l(y_i,\hat{y}^{(t-1)})
\]
\[
h_i=\partial_{\hat{y}^{t-1}}^2l(y_i,\hat{y}^{(t-1)})
\]
\[
l(y_i,\hat{y}_{i})
\]
l表示前t-1棵树组成的学习模型的预测误差,gi、hi分别表示预测误差对当前模型的一阶导和二阶导，当前模型往预测误差减小的方向进行迭代。
对于f(x),需要明确对于一棵树，由两部分来确定，一是树的结构，这个结构将输入样本映射到确定的叶子节点上，记为\[q(x)\],第二部分是各个叶子节点的值，也就是权重，记为\[w_{q(x)}\]。所以（6）式中，
\[
f_{t}(x) = w_{q(x)} \quad \text{(7)}
\]

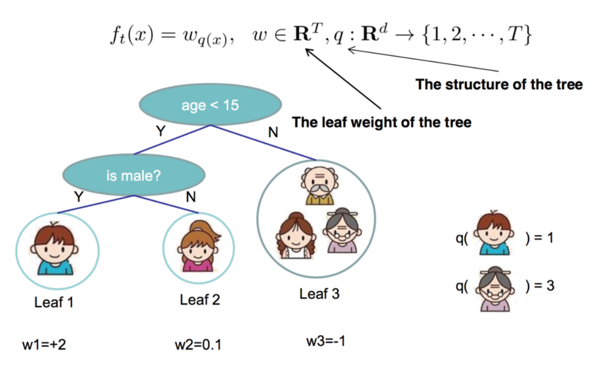
从上图中可以很好的明确q和w的含义。

4.树的复杂度定义

Xgboost包含多棵树，定义每棵树的复杂度：
\[
\Omega(f) = \gamma T + \frac{1}{2}\lambda||w||^2
\]
其中T为叶子节点的个数，||w||为叶子节点向量的模。γ表示节点切分的难度，λ表示L2正则化系数。
那么对于整棵树复杂度的定义：
\[
\Omega(f_{(t)}) = \gamma T + \frac{1}{2}\lambda\sum_{j=1}^{T}w_{j}^2 \quad \text{(8)}
\]

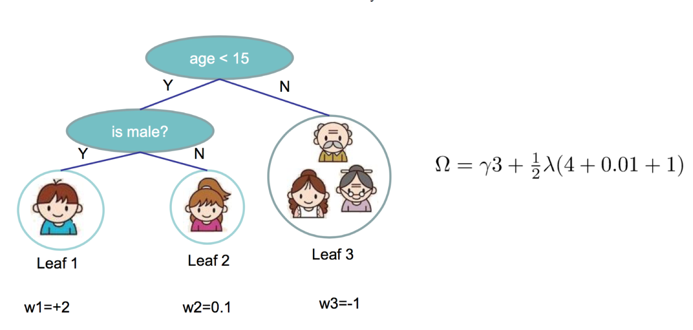
如图可以算出当前树的复杂度\[\Omega\],同时，定义属于叶子结点j 的样本集合为\[I_{j}\]:
\[
I_{j} = \{i|q(x_{i}) = j\}
\]

5.目标函数推导

根据（6）式：
\[
obj(t) \simeq \sum_{i=1}^n[l(y_i,\hat{y}^{t-1})+g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+ \Omega(f(t)) + Constant \quad
\]
其中\[l(y_i,\hat{y}^{t-1})\]是常数，代入（7），(8)式和\[I_{j}\]并忽略常数项，得：
\[
obj(t) = \sum_{i=1}^n[g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)] + \gamma T + \frac{1}{2}\lambda\sum_{j=1}^{T}w_{j}^2 \quad \text{(9)}
\]
\[
\quad\quad\quad = \sum_{i
=1}^n[g_iw_{q(x_i)}+\frac{1}{2}h_iw^2_{q(x_i)}] + \gamma T + \frac{1}{2}\lambda\sum_{j=1}^{T}w_{j}^2 \quad \text{(10)}
\]
\[
\quad\quad= \sum_{j
=1}^T[(\sum_{i\in{I_j}}g_i)w_j+ \frac{1}{2} (\sum_{i\in{I_j}}h_i+\lambda)w_j^2] + \gamma T \quad \text{(11)}
\]
令
\[
G_j=\sum_{i\in{I_j}}g_i \quad h_j=\sum_{i\in{I_j}}h_i
\]
Gj 表示映射为叶子节点 j 的所有输入样本的一阶导之和，同理，Hj表示二阶导之和。则（11）式为：
\[
obj(t)= \sum_{j=1}^T[G_jw_j+ \frac{1}{2}(H_j+\lambda)w_j^2] + \gamma T \quad \text{(12)}
\]
对于第 t 棵C树的某一个确定结构（可用q(x)表示），其叶子节点是相互独立的，Gj和Hj是确定量，因此，（12）可以看成是关于叶子节点的一元二次函数。最小化（12）式即二次函数通过一阶导得0求极值，得参数w的估计：
\[
w_j^* = -\frac{G_j}{H_j+\lambda}
\]
代入到（12）式得到最终的目标函数：
\[
obj(t)= -\frac{1}{2}\sum_{j=1}^{T}\frac{G_j^2}{H_j+\lambda}+\gamma T \quad \text{(13)}
\]
上式也称为打分函数(scoring function)，它是衡量树结构好坏的标准，值越小，代表这样的结构越好。我们用打分函数选择最佳切分点，从而构建一棵CART树。

6.寻找分割点的贪心算法

对于每一个叶结点，根据增益分裂结点。增益的定义：
\[
obj(t)= \frac{1}{2}[\frac{G_J^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}] - \gamma
\quad \text{(14)}
\]
这个公式通常被用于评估分割候选集（选择最优分割点），其中前两项分别是切分后左右子树的的分支之和，第三项是未切分前该父节点的分数值，最后一项是引入额外的叶子节点导致的复杂度。

这里有一个问题，在分裂结点的时候，如何找到该次分裂最佳的分割点呢。实现方法是：遍历所有特征，对每个特征将样本按这个特征排好序，从左向右，依次遍历。每次遍历，向左边加入一个结点，向右边减掉这个结点，然后计算此时的gaingain。最后选择gaingain最大的特征的最佳分割点作为该次分裂的分割点。

所以时间复杂度:O(nlogndk)。对于每一层，需要nlogn的时间去对特征值进行排序，假设有d个特征，树的层数为k层。

7.XGBoost与GDBT的区别

GBDT以CART为基分类器，XGB则支持多种分类器，可以通过booster[default=gbtree]设置参数：gbtree:tree-based models;gblinear:linear models。
GBDT只用到了一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶与二阶导数，并且可以自定义代价函数，只要一阶二阶可导。
XGBoost与GDBT都是逐次迭代来提高模型性能，但是XGBoost在选取最佳切分点时可以开启多线程进行，大大提高了运行速度。（也就是可并行）
新增了Shrinkage和column subsampling，为了防止过拟合。
对缺失值有自动分裂处理（默认归于左子树）。
xgb生成树时，考虑了树的复杂度 -- 预剪枝。
GBDT是在生成完后才考虑复杂度的惩罚 -- 后剪枝。（个人理解）

参考资料：

https://blog.csdn.net/yinyu19950811/article/details/81079192

陈天奇大神-https://www.kdd.org/kdd2016/papers/files/rfp0697-chenAemb.pdf

https://blog.csdn.net/shitaixiaoniu/article/details/53161348

https://baijiahao.baidu.com/s?id=1620689507114988717&wfr=spider&for=pc