[Reinforcement Learning] Model-Free Prediction

上篇文章介绍了 Model-based 的通用方法——动态规划，本文内容介绍 Model-Free 情况下 Prediction 问题，即 "Estimate the value function of an unknown MDP"。

• Model-based：MDP已知，即转移矩阵和奖赏函数均已知
• Model-Free：MDP未知

蒙特卡洛学习

蒙特卡洛方法（Monte-Carlo Methods，简称MC）也叫做蒙特卡洛模拟，是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。其实本质就是，通过尽可能随机的行为产生后验，然后通过后验来表征目标系统。

如下图为使用蒙特卡罗方法估算 \(\pi\) 值，放置30000个随机点后，\(\pi\) 的估算值与真实值相差0.07%。

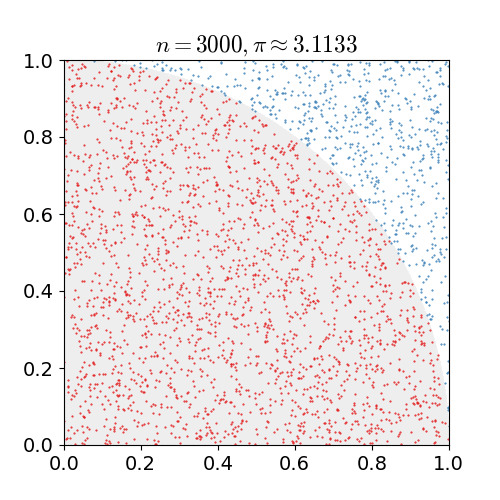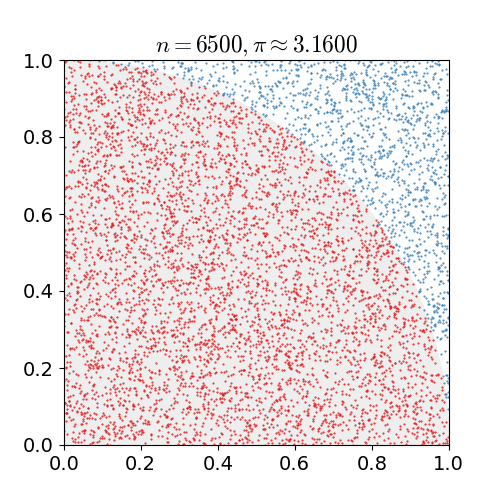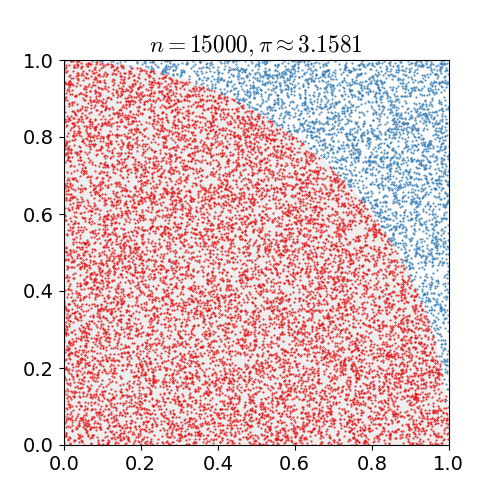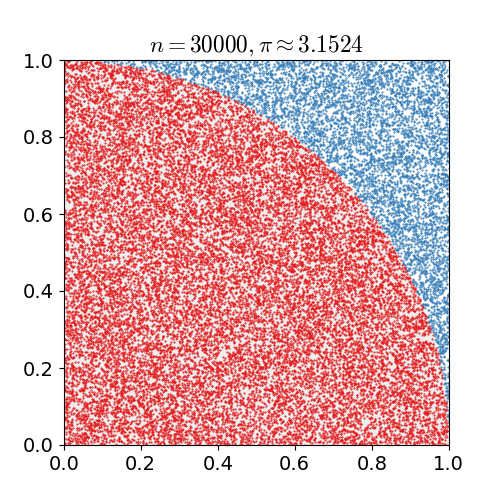
在Model-Free的情况下，MC在强化学习中的应用就是获取价值函数，其特点如下：

• MC 可以从完整的 episodes 中学习（no bootstrapping）
• MC 以均值来计算价值，即 value = mean(return)
• MC 只能适用于 episodic MDPs（有限MDPs）

First-Visit 蒙特卡洛策略评估

First-Visit Monte-Carlo Policy Evaluation：

评估状态 \(s\) 在给定策略 \(\pi\) 下的价值函数 \(v_{\pi}(s)\) 时，在一次 episode 中，状态 \(s\) 在时刻 \(t\) 第一次被访问时，计数器 \(N(s) ← N(s) + 1\)，累计价值 \(S(s) ← S(s) + G_t\)
当整个过程结束后，状态 \(s\) 的价值 \(V(s) = \frac{S(s)}{N(s)}\)
根据大数定理（Law of Large Numbers）：\(V(s) → v_{\pi}(s) \text{ as } N(s) → \infty\)

Every-Visit 蒙特卡洛策略评估

Every-Visit Monte-Carlo Policy Evaluation：

评估状态 \(s\) 在给定策略 \(\pi\) 下的价值函数 \(v_{\pi}(s)\) 时，在一次 episode 中，状态 \(s\) 在时刻 \(t\) 每次被访问时，计数器 \(N(s) ← N(s) + 1\)，累计价值 \(S(s) ← S(s) + G_t\)
当整个过程结束后，状态 \(s\) 的价值 \(V(s) = \frac{S(s)}{N(s)}\)
根据大数定理（Law of Large Numbers）：\(V(s) → v_{\pi}(s) \text{ as } N(s) → \infty\)

Incremental Monte-Carlo

我们先看下增量式求平均：
The mean \(\mu_1, \mu_2, ...\) of a sequence \(x_1, x_2, ...\) can be computed incrementally：
\[
\begin{align}
\mu_k
&= \frac{1}{k}\sum_{j=1}^{k}x_j\\
&= \frac{1}{k}\Bigl(x_k+\sum_{j=1}^{k-1}x_j \Bigr)\\
&= \frac{1}{k}(x_k + (k-1)\mu_{k-1})\\
&= \mu_{k-1} + \frac{1}{k}(x_k - \mu_{k-1})
\end{align}
\]

根据上式我们可以得出增量式进行MC更新的公式：
每次 episode 结束后，增量式更新 \(V(s)\)，对于每个状态 \(S_t\)，其对应的 return 为 \(G_t\)
\[
N(S_t) ← N(S_t) + 1 \\
V(S_t) ← V(S_t) + \frac{1}{N(S_t)}(G_t - V(S_t))
\]

在非静态问题中，更新公式形式可以改为如下：
\[V(S_t) ← V(S_t) + \alpha (G_t - V(S_t))\]

时序差分学习

时序差分方法（Temporal-Difference Methods，简称TD）特点：

• TD 可以通过 bootstrapping 从非完整的 episodes 中学习
• TD updates a guess towards a guess

TD(λ)

下图为 TD target 在不同 n 下的示意图：

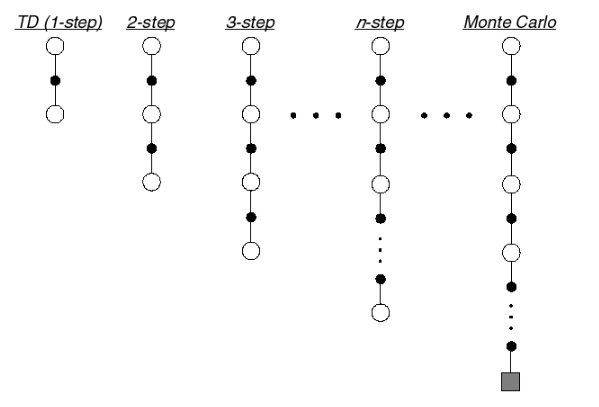
从上图可以看出，当 n 达到终止时，即为一个episode，此时对应的方法为MC，因此从这个角度看，MC属于TD的特殊情况。

n-step Return

n-step returns 可以表示如下：
\(n=1\) 时：\(G_{t}^{(1)} = R_{t+1} + \gamma V(S_{t+1})\)
\(n=2\) 时：\(G_{t}^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2})\)
...
\(n=\infty\) 时：\(G_{t}^{\infty} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1} R_T)\)
因此，n-step return \(G_{t}^{(n)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n}V(S_{t+n}))\)

n-step TD 更新公式：
\[V(S_t) ← V(S_t) + \alpha (G_t^{(n)} - V(S_t))\]

Forward View of TD(λ)

我们能否把所有的 n-step return 组合起来？答案肯定是可以，组合后的return被称为是\(\lambda\)-return，其中\(\lambda\)是为了组合不同的n-step returns引入的权重因子。

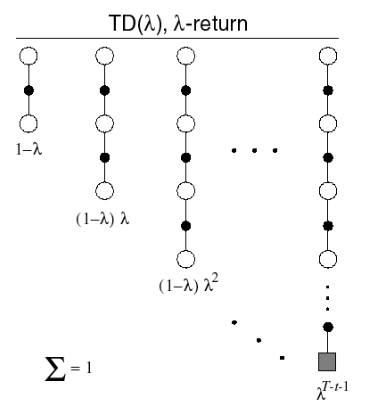
\(\lambda\)-return:
\[G_t^{\lambda} = (1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}G_t^{(n)}\]

Forward-view TD(\(\lambda\))：
\[V(S_t) ← V(S_t) + \alpha\Bigl(G_t^{\lambda} - V(S_t)\Bigr)\]

TD(\(\lambda\))对应的权重公式为 \(( 1-\lambda)\lambda^{n-1}\)，分布图如下所示：

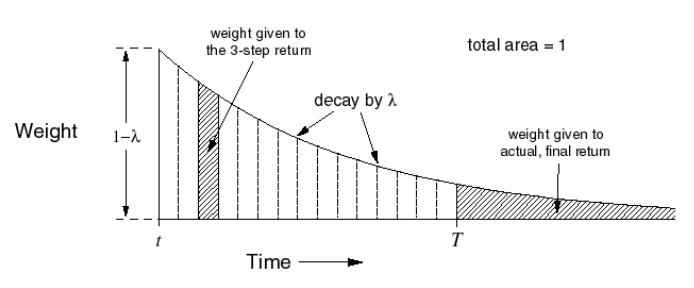
Forward-view TD(\(\lambda\))的特点：

• Update value function towards the λ-return
• Forward-view looks into the future to compute \(G_t^{\lambda}\)
• Like MC, can only be computed from complete episodes

Backward View TD(λ)

• Forward view provides theory
• Backward view provides mechanism
• Update online, every step, from incomplete sequences

带有资格迹的TD(\(\lambda\))：
\[
\delta_t = R_{t+1} + \gamma V(S_{t+1} - V(S_t))\\
V(s) ← V(s) + \alpha \delta_t E_t(s)
\]
其中\(\delta_t\)为TD-error，\(E_t(s)\)为资格迹。

资格迹(Eligibility Traces)

资格迹本质就是对于频率高的，最近的状态赋予更高的信任（credit）/ 权重。

下图是对资格迹的一个描述：

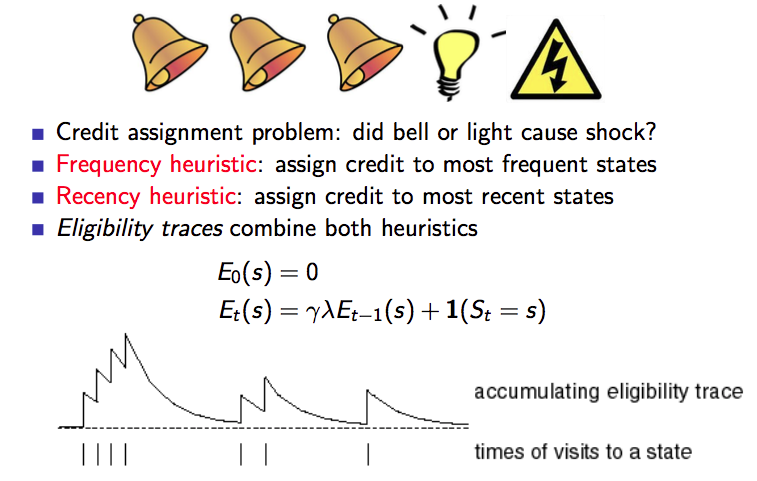
关于TD(\(\lambda\))有一个结论：

The sum of offline updates is identical for forward-view and backward-view TD(λ).

这一块的内容不再深入介绍了，感兴趣的可以看Sutton的书和David的教程。

蒙特卡洛学习 vs. 时序差分学习

MC与TD异同点

相同点：都是从经验中在线的学习给定策略 \(\pi\) 的价值函数 \(v_{\pi}\)

不同点：

• Incremental every-visit Monte-Carlo：朝着真实的 return \(\color{Red}{G_t}\) 更新 \(V(S_t)\)
  \[V(S_t) ← V(S_t) + \alpha (\color{Red}{G_t} - V(S_t))\]
• Simplest temporal-difference learning algorithm: TD(0)
  • 朝着已预估的 return \(\color{Red}{R_{t+1} + \gamma V(S_{t+1})}\) 更新 \(V(S_t)\)
    \[V(S_t) ← V(S_t) + \alpha (\color{Red}{R_{t+1} + \gamma V(S_{t+1})} - V(S_t))\]
  • \(\color{Red}{R_{t+1} + \gamma V(S_{t+1})}\) 称为是 TD target
  • \(\color{Red}{R_{t+1} + \gamma V(S_{t+1})} - V(S_t)\) 称为是 TD error

下图以 Drive Home 举例说明两者的不同，MC 只能在回家后才能改变对回家时间的预判，而 TD 在每一步中不断根据实际情况来调整自己的预判。

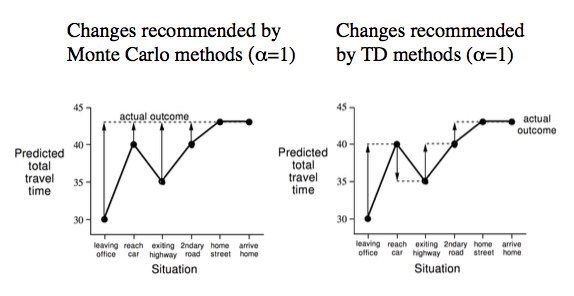
MC与TD优缺点

学习方式

• TD 可以在知道最后结果之前学习（如上图举例）
  • TD can learn online after every step
  • MC must wait until end of episode before return is known
• TD 可以在不存在最后结果的情况下学习（比如无限/连续MDPs）
  • TD can learn from incomplete sequences
  • MC can only learn from complete sequences
  • TD works in continuing (non-terminating) environments
  • MC only works for episodic (terminating) environments

方差与偏差

• MC has high variance, zero bias（高方差，零偏差）
  • Good convergence properties
  • Not very sensitive to initial value
  • Very simple to understand and use
• TD has low variance, some bias（低方差，存在一定偏差）
  • Usually more efficient than MC
  • TD(0) converges to \(v_{\pi}(s)\)
  • More sensitive to initial value

关于 MC 和 TD 中方差和偏差问题的解释：

• MC 更新基于真实的 return \(G_t = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1}R_{T}\) 是 \(v_{\pi}(S_t)\) 的无偏估计。
• 真实的TD target \(R_{t+1} + \gamma v_{\pi}(S_{t+1})\) 也是 \(v_{\pi}(S_t)\) 的无偏估计。但是实际更新时用的 TD target \(R_{t+1} + \gamma V(S_{t+1})\) 是 \(v_{\pi}(S_t)\) 的有偏估计。
• TD target 具有更低的偏差：
  • Return 每次模拟依赖于许多的随机动作、转移概率以及回报
  • TD target 每次只依赖一次随机动作、转移概率以及回报

马尔可夫性

• TD exploits Markov property
  • Usually more efficient in Markov environments
• MC does not exploit Markov property
  • Usually more effective in non-Markov environments

DP、MC以及TD(0)

首先我们从 backup tree 上去直观地认识三者的不同。

• DP backup tree：Full-Width step（完整的step）

  

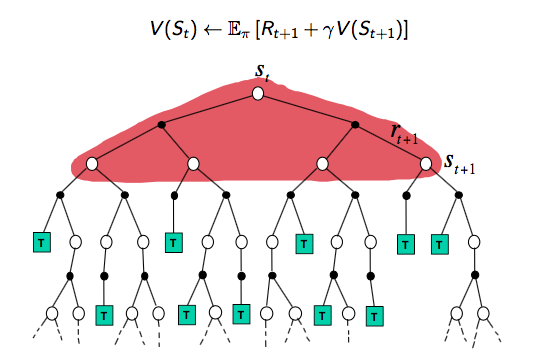
• MC backup tree：完整的episode

  

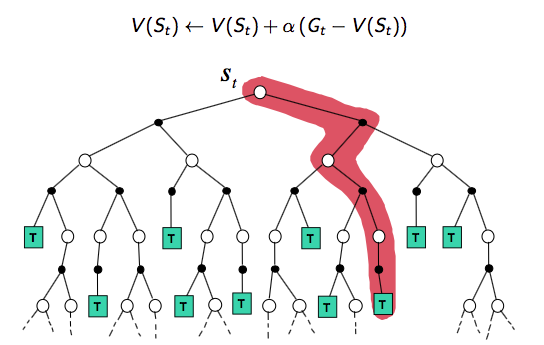
• TD(0) backup tree：单个step

  

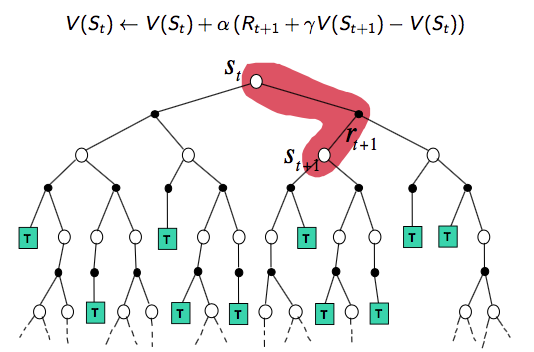
Bootstrapping vs. Sampling

Bootstrapping：基于已预测的值进行更新

• DP bootstraps
• MC does not bootstrap
• TD bootstraps

Sampling：基于采样的期望来更新

• DP does not sample（model-based methods don't need sample）
• MC samples（model-free methods need sample）
• TD samples（model-free methods need sample）

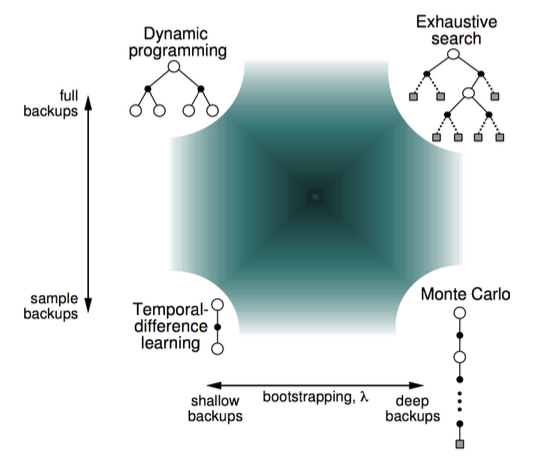
下图从宏观的视角显示了 RL 的几种基本方法的区别：

Reference

[1] 维基百科-蒙特卡洛方法
[2] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018
[3] David Silver's Homepage