R语言 逐步回归分析

逐步回归分析是以AIC信息统计量为准则，通过选择最小的AIC信息统计量，来达到删除或增加变量的目的。

R语言中用于逐步回归分析的函数 step()    drop1()     add1()

#1.载入数据 首先对数据进行多元线性回归分析

tdata<-data.frame(
  x1=c( , ,,, ,, , , ,, ,,),
  x2=c(,,,,,,,,,,,,),
  x3=c( ,, , , , ,,,, ,, , ),
  x4=c(,,,,,, ,,,,,,),
  Y =c(78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,
       93.1,115.9,83.8,113.3,109.4)
)
tlm<-lm(Y~x1+x2+x3+x4,data=tdata)
summary(tlm)

多元线性回归结果分析

通过观察，回归方程的系数都没有通过显著性检验

#2.逐步回归分析

tstep<-step(tlm)
summary(tstep)

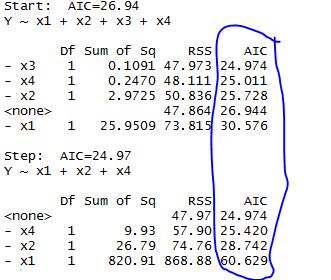
结果分析：当用x1 x2 x3 x4作为回归方程的系数时，AIC的值为26.94

去掉x3 回归方程的AIC值为24.974；去掉x4 回归方程的AIC值为25.011……

由于去x3可以使得AIC达到最小值，因此R会自动去掉x3;

去掉x3之后 AIC的值都增加 逐步回归分析终止  得到当前最优的回归方程

回归系数的显著性水平有所提高 但是x2 x4的显著性水平仍然不理想

#3.逐步回归分析的优化

drop1(tstep)

结果分析

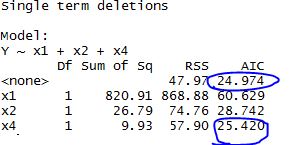
如果去掉x4 AIC的值从24.974增加到25.420 是三个变量中增加最小的

#4.进一步进行多元回归分析

tlm<-lm(Y~x1+x2,data=tdata)
summary(tlm)

结果分析

所有的检验均为显著

因此所得回归方程为y=52.57735+ 1.46831x1+ 0.66225x2.