伸展树--java

文字转载自：http://www.cnblogs.com/vamei

代码转载自：http://www.blogjava.net/javacap/archive/2007/12/19/168627.html

我们讨论过，树的搜索效率与树的深度有关。二叉搜索树的深度可能为n，这种情况下，每次搜索的复杂度为n的量级。AVL树通过动态平衡树的深度，单次搜索的复杂度为log(n) (以上参考纸上谈兵 AVL树)。我们下面看伸展树(splay tree)，它对于m次连续搜索操作有很好的效率。

伸展树会在一次搜索后，对树进行一些特殊的操作。这些操作的理念与AVL树有些类似，即通过旋转，来改变树节点的分布，并减小树的深度。但伸展树并没有AVL的平衡要求，任意节点的左右子树可以相差任意深度。与二叉搜索树类似，伸展树的单次搜索也可能需要n次操作。但伸展树可以保证，m次的连续搜索操作的复杂度为mlog(n)的量级，而不是mn量级。

具体来说，在查询到目标节点后，伸展树会不断进行下面三种操作中的一个，直到目标节点成为根节点 （注意，祖父节点是指父节点的父节点）

1. zig: 当目标节点是根节点的左子节点或右子节点时，进行一次单旋转，将目标节点调整到根节点的位置。

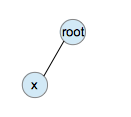
zig

2. zig-zag: 当目标节点、父节点和祖父节点成"zig-zag"构型时，进行一次双旋转，将目标节点调整到祖父节点的位置。

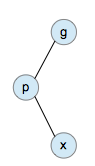
zig-zag

3. zig-zig：当目标节点、父节点和祖父节点成"zig-zig"构型时，进行一次zig-zig操作，将目标节点调整到祖父节点的位置。

zig-zig

单旋转操作和双旋转操作见AVL树。下面是zig-zig操作的示意图:

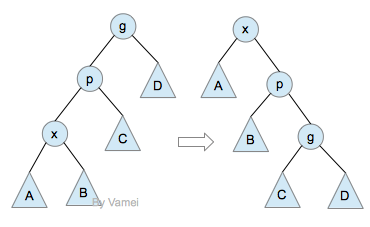
zig-zig operation

在伸展树中，zig-zig操作(基本上)取代了AVL树中的单旋转。通常来说，如果上面的树是失衡的，那么A、B子树很可能深度比较大。相对于单旋转(想一下单旋转的效果)，zig-zig可以将A、B子树放在比较高的位置，从而减小树总的深度。

下面我们用一个具体的例子示范。我们将从树中搜索节点2：

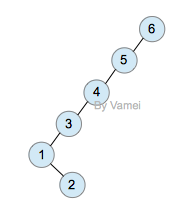
Original

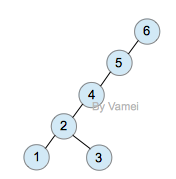
zig-zag (double rotation)

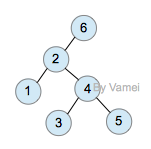
zig-zig

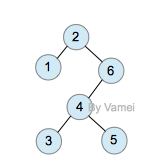
zig (single rotation at root)

上面的第一次查询需要n次操作。然而经过一次查询后，2节点成为了根节点，树的深度大减小。整体上看，树的大部分节点深度都减小。此后对各个节点的查询将更有效率。

伸展树的另一个好处是将最近搜索的节点放在最容易搜索的根节点的位置。在许多应用环境中，比如网络应用中，某些固定内容会被大量重复访问(比如江南style的MV)。伸展树可以让这种重复搜索以很高的效率完成。

java代码：

package algorithms.tree;

/**
 * @author yovn
 *
 */
public class SplayTree<E extends Comparable<E>> extends DefaultBSTree<E> implements BSTree<E> {

    static class SplayTreeNode<E extends Comparable<E>> extends BSTNode<E>
    {

        SplayTreeNode<E> parent;

        SplayTreeNode(SplayTreeNode<E> parent,E key) {
            super(key);
            this.parent=parent;

        }

    }

    @Override
    public boolean delete(E ele) {
          return _delete((SplayTreeNode<E>)root,ele);
    }

    private boolean _delete(SplayTreeNode<E> pointer, E ele) {
        int cmp=ele.compareTo(pointer.key);
        while(cmp!=0)
        {
            if(cmp<0)
            {
                pointer=(SplayTreeNode<E>)pointer.left;
            }
            else
            {
                pointer=(SplayTreeNode<E>)pointer.right;
            }
            if(pointer==null)return false;
            cmp=ele.compareTo(pointer.key);
        }
        //okay find it
        SplayTreeNode<E> p=pointer.parent;
        if(pointer.left==null)
        {
            if(p!=null)
            {
                keep_right(pointer);
                splay(p);
            }
            else {
                root = p.right;
                if(root!=null)((SplayTreeNode<E>)root).parent=null;
            }

        }
        else if(pointer.right==null)
        {
            if(p!=null)
            {
                keep_left(pointer);
                splay(p);
            }
            else {
                root = p.left;
                if(root!=null)((SplayTreeNode<E>)root).parent=null;
            }
        }
        else
        {
            SplayTreeNode<E> todo=(SplayTreeNode<E>)pointer.left;
            SplayTreeNode<E> todoP=null;
            while(todo.right!=null)
            {
                todoP=todo;
                todo=(SplayTreeNode<E>)todo.right;
            }
            pointer.key=todo.key;
            if (todoP != null) {
                todoP.right = todo.left;
                if (todo.left != null)
                    ((SplayTreeNode<E>) todo.left).parent = todoP;
            }
            else
            {
                pointer.left=null;
            }
            splay(pointer.parent);

        }
        return true;
    }

    private void keep_left(SplayTreeNode<E> pointer) {
        SplayTreeNode<E> p=pointer.parent;
        if(p.left==pointer)
        {
            p.left=pointer.left;
            if(p.left!=null)((SplayTreeNode<E>)p.left).parent=p;
        }
        else if(p.right==pointer)
        {
            p.right=pointer.left;
            if(p.right!=null)((SplayTreeNode<E>)p.right).parent=p;
        }

    }

    private void keep_right(SplayTreeNode<E> pointer) {
        SplayTreeNode<E> p=pointer.parent;
        if(p.left==pointer)
        {
            p.left=pointer.right;
            if(p.left!=null)((SplayTreeNode<E>)p.left).parent=p;
        }
        else if(p.right==pointer)
        {
            p.right=pointer.right;
            if(p.right!=null)((SplayTreeNode<E>)p.right).parent=p;
        }

    }

    protected void splay(SplayTreeNode<E> cur) {

        if(cur==null)return;

        while(cur!=root)
        {
            if(cur.parent==root)
            {
                //single Rotation
                SingleRotation(cur,cur.parent);
                cur.parent=null;
                root=cur;

            }
            else if(cur.parent.left==cur&&cur.parent.parent.left==cur.parent)
            {

                cur=Left_ZigZig(cur,cur.parent,cur.parent.parent);

            }
            else if(cur.parent.right==cur&&cur.parent.parent.right==cur.parent)
            {
                cur=Right_ZigZig(cur,cur.parent,cur.parent.parent);
            }
            else if(cur.parent.left==cur&&cur.parent.parent.right==cur.parent)
            {
                cur=RL_ZigZag(cur,cur.parent,cur.parent.parent);
            }
            else if(cur.parent.right==cur&&cur.parent.parent.left==cur.parent)
            {
                cur=LR_ZigZag(cur,cur.parent,cur.parent.parent);
            }
            else
            {
                System.out.println("Oooops!!!");
            }
        }
    }

    private SplayTreeNode<E> LR_ZigZag(SplayTreeNode<E> cur,
            SplayTreeNode<E> p, SplayTreeNode<E> g) {
        SplayTreeNode<E> gp=g.parent;

        g.left=cur.right;
        setParent(cur.right,g);

        g.parent=cur;
        cur.right=g;

        p.right=cur.left;
        setParent(cur.left,p);

        p.parent=cur;
        cur.left=p;
        if(gp!=null)
        {
            if(gp.left==g)
            {
                gp.left=cur;
            }
            else
            {
                gp.right=cur;

            }
        }
        else root=cur;
        cur.parent=gp;
        return cur;
    }

    private SplayTreeNode<E> RL_ZigZag(SplayTreeNode<E> cur,
            SplayTreeNode<E> p, SplayTreeNode<E> g) {
        SplayTreeNode<E> gp=g.parent;

        g.right=cur.left;
        setParent(cur.left,g);

        g.parent=cur;
        cur.left=g;

        p.left=cur.right;
        setParent(cur.right,p);

        p.parent=cur;
        cur.right=p;
        if(gp!=null)
        {
            if(gp.left==g)
            {
                gp.left=cur;
            }
            else
            {
                gp.right=cur;

            }
        }
        else root=cur;
        cur.parent=gp;
        return cur;
    }

    protected SplayTreeNode<E> Right_ZigZig(SplayTreeNode<E> cur, SplayTreeNode<E> p,
            SplayTreeNode<E> g) {
        SplayTreeNode<E> gp=g.parent;

        g.right=p.left;
        setParent(p.left,g);

        p.right=cur.left;
        setParent(cur.left,p);

        g.parent=p;
        p.left=g;

        p.parent=cur;
        cur.left=p;
        if(gp!=null)
        {
            if(gp.left==g)
            {
                gp.left=cur;
            }
            else
            {
                gp.right=cur;

            }
        }
        else root=cur;
        cur.parent=gp;
        return cur;

    }

    protected SplayTreeNode<E> Left_ZigZig(SplayTreeNode<E> cur, SplayTreeNode<E> p,
            SplayTreeNode<E> g) {
        SplayTreeNode<E> gp=g.parent;
        g.left=p.right;
        setParent(p.right,g);

        g.parent=p;
        p.right=g;

        p.left=cur.right;
        setParent(cur.right,p);

        p.parent=cur;
        cur.right=p;
        if(gp!=null)
        {
            if(gp.left==g)
            {
                gp.left=cur;
            }
            else
            {
                gp.right=cur;

            }
        }
        else root=cur;
        cur.parent=gp;
        return cur;

    }

    final void setParent(BSTNode<E> c, BSTNode<E> p) {
        if(c!=null)((SplayTreeNode<E>)c).parent=(SplayTreeNode<E>)p;

    }

    private void SingleRotation(SplayTreeNode<E> cur, SplayTreeNode<E> p) {
        if(p.left==cur)
        {

            p.left=cur.right;
            if(cur.right!=null)((SplayTreeNode<E>)cur.right).parent=p;
            cur.right=p;
            p.parent=cur;

        }
        else if(p.right==cur)
        {
            p.right=cur.left;
            if(cur.left!=null)((SplayTreeNode<E>)cur.left).parent=p;
            cur.left=p;
            p.parent=cur;

        }

    }

    @Override
    public void insert(E ele) {

        if (root == null) {
            root = new SplayTreeNode<E>(null,ele);
            return;
        }
        _insert((SplayTreeNode<E>)root,ele);
    }

    private final void _insert(SplayTreeNode<E> pointer,E ele)
    {

        int cmp=pointer.key.compareTo(ele);
        if(cmp==0)
        {
            throw new IllegalArgumentException();
        }

        if(cmp>0)
        {
            if(pointer.left==null)
            {
                pointer.left =new SplayTreeNode<E>(pointer,ele);
                splay((SplayTreeNode<E>)pointer.left);
                return;
            }
             _insert((SplayTreeNode<E>)pointer.left,ele);

        }
        else
        {
            if(pointer.right==null)
            {
                pointer.right=new SplayTreeNode<E>(pointer,ele);
                splay((SplayTreeNode<E>)pointer.right);
                return ;
            }
            _insert((SplayTreeNode<E>)pointer.right,ele);
        }
    }

    @Override
    public boolean search(E ele) {
        return _search((SplayTreeNode<E>)root,ele);
    }

    private boolean _search(SplayTreeNode<E> pointer, E ele) {
        if(pointer==null)return false;
        int cmp=pointer.key.compareTo(ele);
        if(cmp==0)
        {
            splay(pointer);
            return true;
        }

        if(cmp>0)
        {

             return _search((SplayTreeNode<E>)pointer.left,ele);

        }
        else
        {

            return _search((SplayTreeNode<E>)pointer.right,ele);
        }
    }

    /**
     *
     */
    public SplayTree() {

    }

}

伸展树java代码