[LeetCode] Rectangle Area 矩形面积

Find the total area covered by two rectilinearrectangles in a 2D plane.

Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.

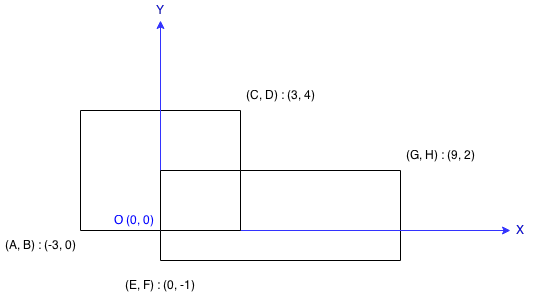
Example:

Input: A = -3, B = 0, C = 3, D = 4, E = 0, F = -1, G = 9, H = 2
Output: 45

Note:

Assume that the total area is never beyond the maximum possible value of int.

Credits:
Special thanks to @mithmatt for adding this problem, creating the above image and all test cases.

这道题不算一道很难的题，但博主还是花了很久才做出来，刚开始尝试找出所以有重叠的情况，发现有很多种情况，很麻烦。后来换了一种思路，尝试先找出所有的不相交的情况，只有四种，一个矩形在另一个的上下左右四个位置不重叠，这四种情况下返回两个矩形面积之和。其他所有情况下两个矩形是有交集的，这时候只要算出长和宽，即可求出交集区域的大小，然后从两个矩型面积之和中减去交集面积就是最终答案。求交集区域的长和宽也不难，由于交集都是在中间，所以横边的左端点是两个矩形左顶点横坐标的较大值，右端点是两个矩形右顶点的较小值，同理，竖边的下端点是两个矩形下顶点纵坐标的较大值，上端点是两个矩形上顶点纵坐标的较小值。之前是可以直接将 sum1 和 sum2 加起来的，可以后来OJ搞了些恶心的 test case，使得直接把 sum1 和 sum2 相加会溢出，所以只好分开了，若两个矩形有重叠，那么返回的时候也不能让 sum1 和 sum2 直接相加，中间一定要先减去重叠部分才行，代码如下：

解法一：

class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int sum1 = (C - A) * (D - B), sum2 = (H - F) * (G - E);
        if (E >= C || F >= D || B >= H || A >= G) return sum1 + sum2;
        return sum1 - ((min(G, C) - max(A, E)) * (min(D, H) - max(B, F))) + sum2;
    }
};

原本上面解法的三行还可以丧心病狂地合成一行，但是由于 OJ 使坏，加了些变态的 test case，使得我们还是得拆分开来，先求出重叠区间的四个点 left，bottom，right，top 的值，然后再求出重叠区间的面积，避免溢出，参见代码如下：

解法二：

class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int left = max(A,E), right = max(min(C,G), left);
        int bottom = max(B,F), top = max(min(D,H), bottom);
        return (C - A) * (D - B) - (right - left) * (top - bottom) + (G - E) * (H - F);
    }
};

Github 同步地址：

https://github.com/grandyang/leetcode/issues/223

类似题目：

Rectangle Overlap

Rectangle Area II

参考资料：

https://leetcode.com/problems/rectangle-area/

https://leetcode.com/problems/rectangle-area/discuss/62149/Just-another-short-way

https://leetcode.com/problems/rectangle-area/discuss/62302/Clean-C%2B%2B-Solution-with-Detailed-Explanations

LeetCode All in One 题目讲解汇总(持续更新中...)