[SCOI2010]生成字符串

题目描述

lxhgww最近接到了一个生成字符串的任务，任务需要他把n个1和m个0组成字符串，但是任务还要求在组成的字符串中，在任意的前k个字符中，1的个数不能少于0的个数。现在lxhgww想要知道满足要求的字符串共有多少个，聪明的程序员们，你们能帮助他吗？

输入输出格式

输入格式：

输入数据是一行，包括2个数字n和m

输出格式：

输出数据是一行，包括1个数字，表示满足要求的字符串数目，这个数可能会很大，只需输出这个数除以20100403的余数

输入输出样例

输入样例#1：

2 2

输出样例#1：

2

说明

limitation

每点2秒

对于30%的数据，保证1<=m<=n<=1000

对于100%的数据，保证1<=m<=n<=1000000

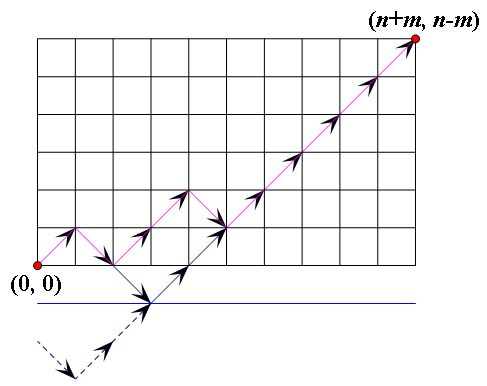
首先，我们设选1为(1,1),选0为(1,-1)

目标就是(n+m,n-m)

总方案数为C(n+m,n)，因为有n+m个位置，放n个1

然后要减去不合法的即线路通过y=-1的。将线路与y=-1交点的左边沿着y=-1做对称操作，则最后等价于从(0,-2)走到(n+m,n-m)的方案数

所以向上走n-m+2

则有x-y=n-m+2

　　x+y=n+m

　　x=n+1,y=m-1

所以不合法方案为C(n+m,n+1)

ans=C(n+m,n)-C(n+m,n+1)

求这些用模逆元，O(n)求解

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 long long A[],B[],ans1,ans2;
 int n,m,Mod=;
 int main()
 {int i,j;
     cin>>n>>m;
     A[]=;
     for (i=;i<=n+m;i++)
      A[i]=((Mod-Mod/i)*A[Mod%i])%Mod;
     for (i=;i<=n+m;i++)
      A[i]=(A[i]*A[i-])%Mod;
      B[]=;
      for (i=;i<=n+m;i++)
      B[i]=(B[i-]*i)%Mod;
      ans1=(((B[n+m]*A[n])%Mod)*A[m])%Mod;
      ans2=(((B[n+m]*A[n+])%Mod)*A[m-])%Mod;
      cout<<(ans1-ans2+Mod)%Mod;
 }