北京大学冯哲清北学堂讲课day1

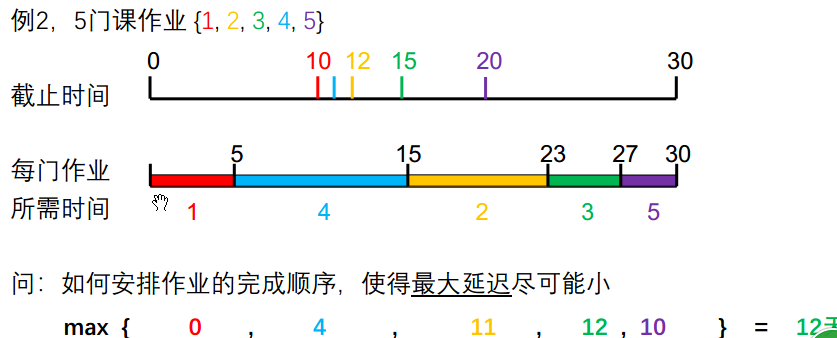
贪心方案：

答案是第三个策略

二分的一个重点是有顺序性，只有满足这个件才可以二分判断区间，否则你得自己构造顺序。

洛谷跳石头同题：

首先，我们要最小化最大跳远距离

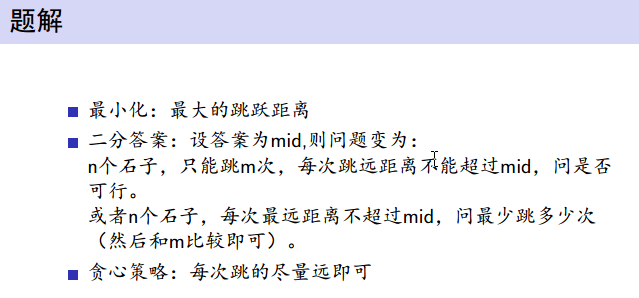
代码如下（此题）

#include<cstdio>
#include<algorithm>
#include<cstring>

#define N 300005

using namespace std;

int i,j,m,n,p,k,a[N],x;//r为right，l为left

int check(int x)//判断mid是否符合条件
{
        int i,cnt=;
        for (i=;i<=n;++i) if (a[i]-a[i-]>x) return ;//x过小，直接右边查找
        for (i=;i<n;)
        {
                for (j=i;j<=n&&a[j]-a[i]<=x;++j);//处理a数组，使判断时改为石头间距离
                ++cnt;//计数器加一
                i=j-;//删除这个点
        }
        if (cnt<=m) return ;
        return ;
}

int main()
{
        scanf("%d%d",&n,&m);
        for (i=;i<=n;++i) scanf("%d",&a[i]);
        sort(a+,a+n+);//从小到大排序石头距离
        int l=,r=(int)1e9,mid=;//数据范围没给，直接定义1e9（反正log1e9也不是很大）
        while ((l+r)>>!=mid)//如果头尾平均数不等于上一次循环的mid（不能再分了，间隔为1时结束循环）
        {
               mid=(l+r)>>;//二分灵魂
               if (check(mid)) r=mid;//返回值为1，就是大了；返回值为0，就是小了
               else l=mid;//返回值为0的话，就取右半边
        }
        printf("%d\n",r);
}

看起来很像贪心是不是？

然而贪心是错的。QWQ

三分：能对单峰函数求峰值

#include<cstdio>
#include<algorithm>
#include<cstring>

#define N 500005

using namespace std;

int i,j,m,n,p,k,a[N],ty,x;

long long b[N];

double check(int x)
{
        return .*(b[x-]+a[n])/x;
}

int main()
{
        scanf("%d",&m);
        for (;m--;)
        {
                scanf("%d",&ty);
                if (ty==)
                {
                        scanf("%d",&x);
                        a[++n]=x;
                        b[n]=b[n-]+x;
                }
                else
                {
                        int l=,r=n;
                        while (r-l>)
                        {
                            int len=(r-l+)/,mid1=l+len,mid2=mid1+len;
                            if (check(mid1)<check(mid2)) r=mid2;
                            else l=mid1;
                        }
                        double ans=;
                        for (i=l;i<=r;++i) ans=max(ans,a[n]-check(i));
                        printf("%.10lf\n",ans);
                }
        }
}

然后；老师开始了分治。

第一题：快速幂

我直接连接我的博客（因为讲的是重复的内容）

https://www.cnblogs.com/lbssxz/p/10656598.html

我这个是取模的运算，你要黈的话去了就行

然后是：

你会发现，红点和中心的那三个黑点是等价的，都不能分。