JVM之GC算法、垃圾收集算法——标记-清除算法、复制算法、标记-整理算法、分代收集算法

标记-清除算法

此垃圾收集算法分为“标记”和“清除”两个阶段：

　　首先标记出所有需要回收的对象，在标记完成后统一回收所有被标记对象，它的标记过程前面已经说过——如何判断对象是否存活/死去

　　死去的对象就会被标记，然后被清除。

它主要有两点不足：

　　一个是效率问题，标记和清除两个过程的效率都不高；

　　另一个是空间问题，标记清除之后会产生大量不连续的空间碎片，空间碎片太多可能会导致以后再程序运行过程中需要分配较大对象时，

　　无法找到足够的连续内存而不得不提前触发另一次垃圾收集动作。

标记-清除算法的执行过程如下图所示：

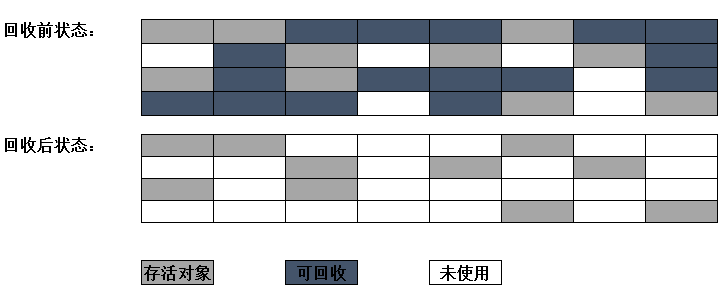
复制算法

　　复制算法的出现，解决了效率问题，它将可用内存按容量划分为大小相等的两块，每次只是用其中的一块。当这一块内存用完了，就将

还存活着的对象复制到另外一块上面，然后再把已使用过的内存空间一次清理掉。这样使得每次都是对整个半区进行内存回收，内存分配时

也就不用考虑内存碎片等复杂情况，只要一动堆顶指针，按顺序分配内存即可，实现简单，运行高效。

　　只是这种算法的代价是将内存缩小为了原来的一半，未免太高了点。

复制算法的执行过程如下图：

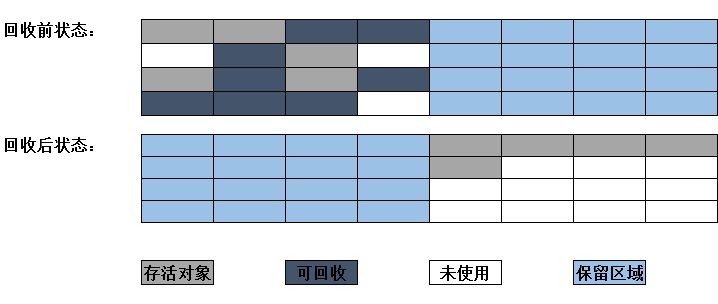
　　现在的商业虚拟机都采用复制算法来回收新生代，IBM公司的专门研究表明，新生代中的对象98%是“朝生夕死”的，所以并不需要按照1:1的

比例来划分内存空间。

　　堆内存中的新生代分为一块较大的Eden空间和两块较小的Survivor空间，详情请看——JVM内存结构/JVM运行时数据区，以及堆内存的划分

每次使用Eden和其中一块From Survivor，当回收时，将Eden和From Survivor中还存活着的对象一次性地复制到另外一块To Survivor空间上，最

后清理掉Eden和刚才用过的From Survivor空间。

　　HotSpot虚拟机默认Eden：From Survivor：To Survivor = 8:1:1 ，也就是每次新生代中可用内存空间为整个新生代容量的90%（80%+10%），

只有10%的内存会被“浪费”。当然，98%的对象可回收只是一般场景下的数据，我们没有办法保证每次回收都只有不多于10%的对象存活，当To

Survivor空间不够用时，需要依赖其它内存（这里指老年代）进行分配担保（Handle Promotion）。

听过某司的一个面试题，为什么新生代中Eden：From Survivor：To Survivor是8:1:1，就可以用上面的内容来解释。

标记-整理算法

　　复制收集算法在对象存活率较高时就要进行较多的复制操作，效率将会变低。更关键的是，如果不想浪费50%的空间，就需要额外的空

间进行分配担保，以应对被使用的内存中所有对象都100%存活的极端情况，所以老年代一般不能直接选用这种算法。

　　根据老年代的特点，有人提出了另外一种“标记-整理”（Mark-Compact）算法，标记过程仍然与“标记-清除”算法一样，但后续步骤不是

直接对可回收对象进行清理，而是让所有存活对象都向一端移动，然后直接清理掉端边界以外的内存。

“标记-整理”算法的执行过程如下图：

分代收集算法

　　当前商业虚拟机的垃圾收集都采用“分代收集”（Generational Collection）算法，这种算法并没有什么新的思想，只是根据对象存活周

期的不同将内存划分为几块。一般是把Java堆分为新生代和老年代，这样就可以根据各个年代的特点采用最合适的收集算法。在新生代中，

每次垃圾收集时都发现有大批对象死去，只有少量存活，那就选用复制算法，只需要付出少量存活对象的复制成本就可以完成收集。而老年

代中因为对象存活率高、没有额外空间对它进行分配担保，就必须使用“标记-整理”算法进行回收。