常用校验码（奇偶校验，海明校验，CRC）学习总结

一.为什么要有校验码？

因为在数据存取和传送的过程中，由于元器件或者噪音的干扰等原因会出现错误，这个时候我们就需要采取相应的措施，发现并纠正错误，对于错误的检测和校正，大多采取“冗余校验”的思想，即除原数据外，额外增加若干位编码，这些新增的代码称为校验位。

二.数据是如何校验的？

输入的数据m经过f得到p校验位。
数据m和校验位一起通过存储器或传输线路，分别得到m'和p'，这两者可能和m,f相同，也可能由于传输储存发生问题而不同。
由数据m'再次经过f得到校验位p''，比较p''和p'，从而得出是否出错，输出对应的信息，如何比较，会在下面的对应校验码中给出。

三.码距

若干位代码组成的一个字称为码字，而两个码字具有不同代码的位数为这两个码字的距离，而码制里各种码字间最小的距离称为码距。

比如8421码，1001和0000，有两位不同，所以距离是2，而0010和0011的距离为1，是最小的距离，故8421码码距为1

那么，码距有什么用呢？答案是码距和这种类型的码的检错，纠错能力有关。

如8421码，由于码距是1，无检错，纠错能力，比如数据0000，如果其中一位变化，变成0001，那么，这个数据仍然是合法的。

再如奇偶校验码中奇校验码，如100000000和010000000，码距为2，我们可以发现，如果数据中有一位变化了，如100000000变为110000000，我们可以很容易地判断出数据出错了，因为110000000不符合奇校验的编码（校验位和数据位一起所含1的个数为奇数）

我们可以发现，校验码可以帮助扩大码距，从而找出错误。

码距与检错、纠错能力的关系（当d≤4）

若码距d为奇数，则能发现d-1位错，或能纠正(d-1)/2位错。
若码距d为偶数，则能发现d/2位错，并能纠正(d/2-1)位错。

四.奇偶校验码

1.编码方式
无论数据位多少位，校验位只有一位
数据位和校验位一共所含的1个数为奇数，称为奇校验
数据位和校验位一共所含的1个数为偶数，称为偶校验

例如（加粗为校验位）：

数据	奇校验的编码	偶校验的编码
00000000	100000000	000000000
01010100	001010100	101010100
01111111	001111111	101111111

由于数据传输过程一般是出现一位错误，而奇偶校验码能发现奇数个错误，所以奇偶校验的实用价值还是很高的。

2.实现原理

那么，奇偶校验是怎么来发现错误的呢？根据二.数据是如何校验的我们可以知道，在数据传输之前，我们会求一次校验位，传输后，会求一次校验位，那么，在奇偶校验中，我们通过比较这两个校验位是否相同，一般是采用异或的方式，若结果为1，则说明有奇数个错误，结果为0，则说明正确或者偶数个错误。

五.海明校验码

1.引入

在了解了奇偶校验码之后，我们可以稍稍做下思考，既然奇偶校验码具有一定的局限性，也就是只能检测奇数的错误，并且不能改正错误，这也就意味着数据一旦传输错误，我们必须要重新上传，那么，我们有办法确定错误发生的位置么？只要确定了错误发生的位置，改正其实就是取反。
这个时候，让我们来看看奇偶校验码，它是在数据的前面或者后面加上以为校验位，那么，如果我们将数据分段，分成某些小段，这样是不是能判断错误发生的位置呢？

2.海明校验码最简单求法

我们以8位数据位，4（5）位校验位为例

我们将海明校验码表示为(H13) H12 H11 H10 H9 H8 H7 H6 H5 H4 H3 H2 H1

其中加粗的部分为校验位，校验位所在位置为2^（i-1），i=1,2,3...

我们还可以把它写成（P5） D8 D7 D6 D5 P4 D4 D3 D2 P3 D1 P2 P1

其中P代表的是校验位，D代表数据位

	12	11	10	9	8	7	6	5	4	3	2	1	S
2^0		D7		D5		D4		D2		D1		P1	S1
2^1		D7	D6			D4	D3			D1	P2		S2
2^2	D8					D4	D3	D2	P3				S3
2^3	D8	D7	D6	D5	P4								S4

我们来看看这个表是怎么画出来的

首先数据位和校验位的位置我们通过公式可以得出
同列数据位所占的位置对应的行的值之和为列的值。举个例子，如D1,所在列为3，所在行分别为2^0和2^1，即1和2,满足式子1+2=3。

校验位的值为同行数据位相异或得到，至于P5，则是由所有数据位和校验位一起异或得到。

3.海明校验码判断修复错误

下面引入一个错误字S的概念

其实错误字S也就是传输前后分别求的校验位的异或值，奇偶校验码只要看一个错误字，而海明校验码则要考虑多个错误字。

S4 ~ S1为全0,说明没错. S4 ~ S1不为全0,说明有错. S5=1说明1位出错,而S5=0说明2位错，不再有效，且不能查出是哪2位出错。

S4~S1的编码值对应的则是出错的海明码位号（不太清楚图表可以返回上面的表格对照）：

如1100，对应D8出错

如1011，对应D7出错

如1010，对应D6出错

如1001，对应D5出错......

Tip：我们通过观察8个数据位4个校验位的海明校验码，发现，若一位出错，则至少有两组校验码的生成收到影响，故我们得到其码距为3，根据码距与检错、纠错能力的关系可以得出该校验码能发现两位错，或修改一位错。

4.校验码位数的确定

前面看完后，一定有人会有疑问，为什么八位数据位我要四位或者五位校验位，三位不行么？六位不行么？那么，请继续看看下面

假定数据位数为n，校验码为k位，则故障字位数也为k位。k位故障字所能表示的状态最多是2K，每种状态可用来说明一种出错情况。

若只有一位错，则结果可能是：

数据中某一位错 (n种可能)

校验码中有一位错 (k种可能)

无错 ( 1 种可能)

假定最多有一位错，则n和k必须满足下列关系：

2^k≥1+n+k，即：2^k-1≥n+k

所以当数据有8位时，校验码和故障字都应有至少4位。

六.循环冗余码（CRC码）

1.为什么大批量数据不用奇偶校验？

在每个字符后增加一位校验位会增加大量的额外开销；尤其在网络通信中，对传输的二进制比特流没有必要再分解成一个个字符，因而无法采用奇偶校验码。

2.模2运算

在介绍CRC码之前，有必要介绍下计算CRC码必要的模2运算：

模2运算不考虑加法进位和减法借位，上商的原则是当部分余数首位是１时商取１，反之商取0。然后按模2相减原则求得最高位后面几位的余数。这样当被除数逐步除完时，最后的余数位数比除数少一位。这样得到的余数就是校验位。

3.基本思想

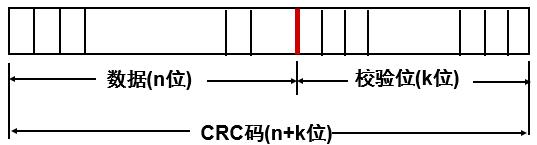
数据信息M(x)为一个n位的二进制数据，将M(x)左移k位后，用一个约定的“生成多项式”G(x)相除，G(x)是一个k+1位的二进制数，相除后得到的k位余数就是校验位。校验位拼接到M(x)后，形成一个n+k位的代码，称该代码为循环冗余校验 ( CRC ) 码，也称（n+k,n）码。

一个CRC码一定能被生成多项式整除，当数据和校验位一起送到接受端后，只要将接受到的数据和校验位用同样的生成多项式相除，如果正好除尽，表明没有发生错误；若除不尽，则表明某些数据位发生了错误。通常要求重传一次。

4.CRC码求法

5.CRC码检错

将收到的CRC码用约定的生成多项式G(x)去除,如果码字无误则余数应位0,如果有某一位出错,则余数不为0,不同位数出错余数不同.