js算法初窥02（排序算法02-归并、快速以及堆排序）

　　上一篇，我们讲述了一些简单的排序算法，其实说到底，在前端的职业生涯中，不涉及node、不涉及后台的情况下，我目前还真的没想到有哪些地方可以用到这些数据结构和算法，但是我在前面的文章也说过了。或许你用不到，但是，真的，如果你想要在前端领域有一个不错的发展。数据结构和算法一定是你的必修课。它不仅仅让你在处理问题的时候可以有一个思维底蕴，更重要的是，在遇到一些奇葩产品的时候，你可以和他PK到底！嗯，到底！

　　哈哈，开个小玩笑。咱们还是聊点有营养的。上一篇的算法比较简单，主内容就是循环，次内容就是比较。但是，这篇文章所介绍的一些算法，在实现上有些许的复杂，甚至在其中涉及到了一部分数据结构相关的知识，如果你对数据结构还不是十分了解，请移步这里用js来实现那些数据结构—目录。

　　那么，我们这篇文章要一起来看看另外一些在执行上有着更高效率的算法，比如归并排序，比如快速排序，还有堆排序等等。

1、归并排序

　　我们先来看看什么是归并排序，以及归并排序是怎么实现的。

　　归并排序属于一种分治算法。归并排序的思想就是将原始数组切分成一个一个较小的数组，直到每一个数组只有一个元素为止，然后再把一个一个小数组，一点一点的结合成一个最终排序后的数组。其实简单来说，就是先分，再合。归并排序的实现有两种方法，一种是递归，一种是迭代。下面我们只用递归的方式来实现一下代码：

　　

//归并排序
// 不多说，你懂的。
this.mergeSort = function () {
    array = mergeSortRec(array);
};
//这个私有函数，其实就是整个归并排序中“分”的部分。我们来看看它是如何“分”的。
var mergeSortRec = function (array) {
    //存储数组长度。
    var length = array.length;
    //由于是递归，所以当length 为 1 的时候，说明我们分到底了。直接返回这个数组。也就是只有一个元素的数组。
    //同时这个判断条件也是递归的终止条件，要记住任何递归操作都必须有终止条件。不然会陷入死循环。
    if(length === 1) {
        return array;
    }
    //我们要把原始数组从中一分为二。下面就是一分为二的操作。无需多说。
    var mid = Math.floor(length / 2),
        left = array.slice(0,mid),
        right = array.slice(mid,length);
    // 这里，我们先不去管merge函数是做什么的。我们先看递归到最底层。merge的两个参数会变成什么。
    // 由于我们又返回了自身，至此递归就形成了。在merge的参数中我们又递归调用了一次自身。
    // 那么这次调用我们把left和right两个数组又拆分了一次。直到最后array.length 为 1（归并的最小单位）。
    // 那么换句话说，实际上merge函数递归的最底层传入的就是两个只有一个元素的数组。
    return merge(mergeSortRec(left),mergeSortRec(right));
};

var merge = function (left,right) {
    // 我们声明一个最终结果的数组result,
    // il和ir是用来控制左右两个数组的迭代的变量
    var result = [],il = 0,ir = 0;

    // 这里，我们的最底层是只有两个只有一个元素的数组
    /*
        array[left]和array[right]
        第一个while， 循环的条件是两个长度变量是否在合法值内。
    */
    while(il < left.length && ir < right.length) {
        // 如果左侧小于右侧，此时的il和ir是相等的都是0。注意这一点
        // 我们就把左侧的left[il]放入数组并il++。否则，我们就把right[ir]存入数组result并ir++。此时，il和ir就不相等了。
        // 所以，这时候，我们下一次循环判断的条件就是递增的ir或il与没有递增的il或者ir做比较。这样就使得一个数组中的一个元素与另外数组中所有元素都做过比较。
        // 希望上面我说明白了想要表达的意思。
        if(left[il] < right[ir]) {
            // 这里，不太容易理解。为什么我们要在result中加入il++而不是il?
            // 其实这里的意思是，先加如left[il]再il++。
            // 不信，你可以把代码改成这个样子
            /*
            result.push(left[il]);
            il++
            */
            // 效果是一样一样的。
            result.push(left[il++]);
        } else {
            result.push(right[ir++]);
        }
    };
    //这两个循环的目的是把剩余的数组元素（包括left数组和right数组）都存入result数组中。
    // 这样我们就行了一个归并后的结果数组，然后进行下一次的归并过程的初始参数。
    while(il < left.length) {
        result.push(left[il++]);
    };

    while(ir < right.length) {
        result.push(right[ir++]);
    };

    return result;
};

//我们用上一章的方法来测试一下归并排序
var arraylist = creatArrayList(5);
console.log(arraylist.toString());//5,4,3,2,1
arraylist.mergeSort();
console.log(arraylist.toString());//1,2,3,4,5

　　其实归并排序的核心思想就是先拆分数组直至分为只有一个元素的数组时，再对其一点一点的进行合并。

2、快速排序

　　快速排序是我们在组织架构或者实际应用中最为常用的排序算法之一，你也可以把快速排序用在你的项目中。

　　快速排序的思想和归并排序有些类似，但是快速排序不需要把拆分开的元素装入一个新的数组，而是直接在原数组上进行交换操作。

　　那么我们来看看快速排序的操作步骤：

　　　　首先我们要找到用于与之相比较的“主元”。理论上主元可以为数组中的任意的元素，但是在本文中我们选取数组的中间项作为主元。

　　　　然后，我们选择主元左侧和右侧的两部分中的元素分别和主元做比较，直到我们找到了左侧比主元大并且右侧比主元小的元素，那么我们就交换两个元素的位置。直到迭代的左侧指针超过了右侧指针。这样，我们就使比主元小的元素和比主元大的元素分别存在于主元的两侧。

　　　　最后，我们再对左右两侧的数组递归重复上面的步骤。直至数组排序结束。

　　我们来看下代码。

//快速排序
this.quickSort = function () {
    // 这里传入的参数是原始数组本身和首尾元素的下标。
    quick(array,0,array.length - 1);
};

var quick = function (array,left,right) {
    // 这个index是为了帮助我们分离出较小值数组和较大值数组的
    var index;
    // 如果length>1才执行逻辑，因为只有一个元素的数组意味着无需排序。
    if(array.length > 1) {
        // partition返回一个元素的下标。
        index = partition(array,left,right);
        //下面两个判断条件为了区分我们要递归的是较小值数组还是较大值数组。
        if(left < index - 1) {
            quick(array,left,index - 1);
        };

        if(index < right) {
            quick(array,index,right);
        };
    }
};
//我们来看看划分过程的这个方法
var partition = function (array,left,right) {
    // pivot（主元），也就是我们要与之比较的元素。我们选取中间项作为主元。
    // i和j代表着较小值数组和较大值数组当前元素的指针
    var pivot = array[Math.floor((right + left) / 2)],i = left,j = right;
    //要知道最开始的i是0，j是lenght-1。所以i++是往右侧移动指针，j--是往左侧移动指针。
    //循环的条件是较小值数组的下标小于较大值数组的下标。
    while(i <= j) {
        // 如果array[i]元素小于主元，向右移动指针。
        while(array[i] < pivot) {
            i++;
        };
        // 如果array[j]元素大于主元，向左移动指针。
        while(array[j] > pivot) {
            j--;
        };
        //上面两个while迭代，当遇到不符合条件的时候就会停下来。
        // 而这种不符合条件的情况是array[i]>array[j]。这是要调整的情况。但是此时i仍旧是小于等于j的。要注意,i在这里不可能比j大。
        // 所以我们此时交换两个下标对应的元素，并改变i和j的指针。最后返回下标i。
        if(i <= j) {
            swap(array,i,j);
            i++;
            j--;
        };
    };

    return i;
};

var arraylist = creatArrayList(5);
console.log(arraylist.toString());//5,4,3,2,1
arraylist.quickSort();
console.log(arraylist.toString());//1,2,3,4,5

　　　　

3、堆排序

　　在说堆排序之前，我们得先了解一下什么是堆，堆这种数据结构本质是一个完全二叉树（如果你还不知道什么是树，请看我前面的文章），那么既然堆是一种树，那么有关于树的一些概念都可以用在堆上面，比如深度，比如节点等。要知道，树通常都会有左孩子又孩子节点和父节点的指针，但是在完全二叉树中，这些指针都可以去掉，因为我们可以用一定的规律来直接找到当前节点的关联节点。比如给定某一个结点，假设它的下标为i，那么它的左孩子结点的下标就是2i + 1，右孩子结点的下标就是2i + 2，它的父结点为(i−1)/2。这样，我们就把可以省略去这些指针，直接将堆中的结点存储在数组中了。

　　在了解了什么是堆之后，我们看看堆排序是怎么操作的。我们直接从代码中看比较具体：

//堆排序
// 这里你需要对树数据结构有一定的了解和认识。如果你对树结构还不是十分了解，请看我前面有关于树结构的相关章节。
// 或者，你可以直接用下面的代码来解决问题，当然，你需要做一些细微的改动。
this.heapSort = function () {
    // 把数组长度存入一个变量
    var heapSize = array.length;
    // 把该数组“堆”化。
    buildHeap(array);
    //迭代递减heapSize的长度，交换数组中下标为0和当前的heapSize重新使变动的堆“合理化”。这里的合理化是指让交换了元素位置的数组重新生成符合堆原理的一个新数组。
    while(heapSize > 1) {
        heapSize--;
        swap(array,0,heapSize);
        heapify(array,heapSize,0);
    };
};
//生成堆函数，我们的i为数组中间值并且递减i的循环为heapify函数传入。
var buildHeap = function (array) {
    var heapSize = array.length;
    for(var i = Math.floor(array.length / 2);i >= 0; i--) {
        heapify(array,heapSize,i);
    };
};
//“堆”化函数。
var heapify = function (array,heapSize,i) {
    //我们声明左节点，右节点，以及父节点（也就是largest）的变量
    var left = i * 2 + 1,
        right = i * 2 + 2,
        largest = i;
    //这两个判断是为了知道在当前轮中的父节点是谁。
    if(left < heapSize && array[left] > array[largest]) {
        largest = left;
    };

    if(right < heapSize && array[right] > array[largest]) {
        largest = right;
    };
    //如果largest变了，我们就需要交换两个值得位置。并且重新调用heapify。
    if(largest !== i) {
        swap(array,i,largest);
        heapify(array,heapSize,largest);
    };
};

var arraylist = creatArrayList(125);
console.log(arraylist.toString());//5,4,3,2,1
arraylist.heapSort();
console.log(arraylist.toString());//1,2,3,4,5

　　堆排序的概念其实并不难理解，唯一需要注意的就是堆数据结构的概念，希望我说清楚了，如果你觉得我对于堆的讲解并不详细，首先你可以百度，其次你可以谷歌，再次你还可以去搜维基百科。实在不行，你去这里看看https://zhuanlan.zhihu.com/p/25820535。这是一篇有关于java相关的系列教程之一。当然，就算你不懂java，相信你也一样可以看懂，真的，我没开玩笑。

　　我在纠结要不要画张图还是就这样结束，因为画一个完整的流程图真的很花时间......我抽根烟考虑下......要不大家去买本书看吧。。。。嗯....一个不错的建议。　

　　下面我们以数组[3,5,1,6,4,7,2]作为图例的基本数据：

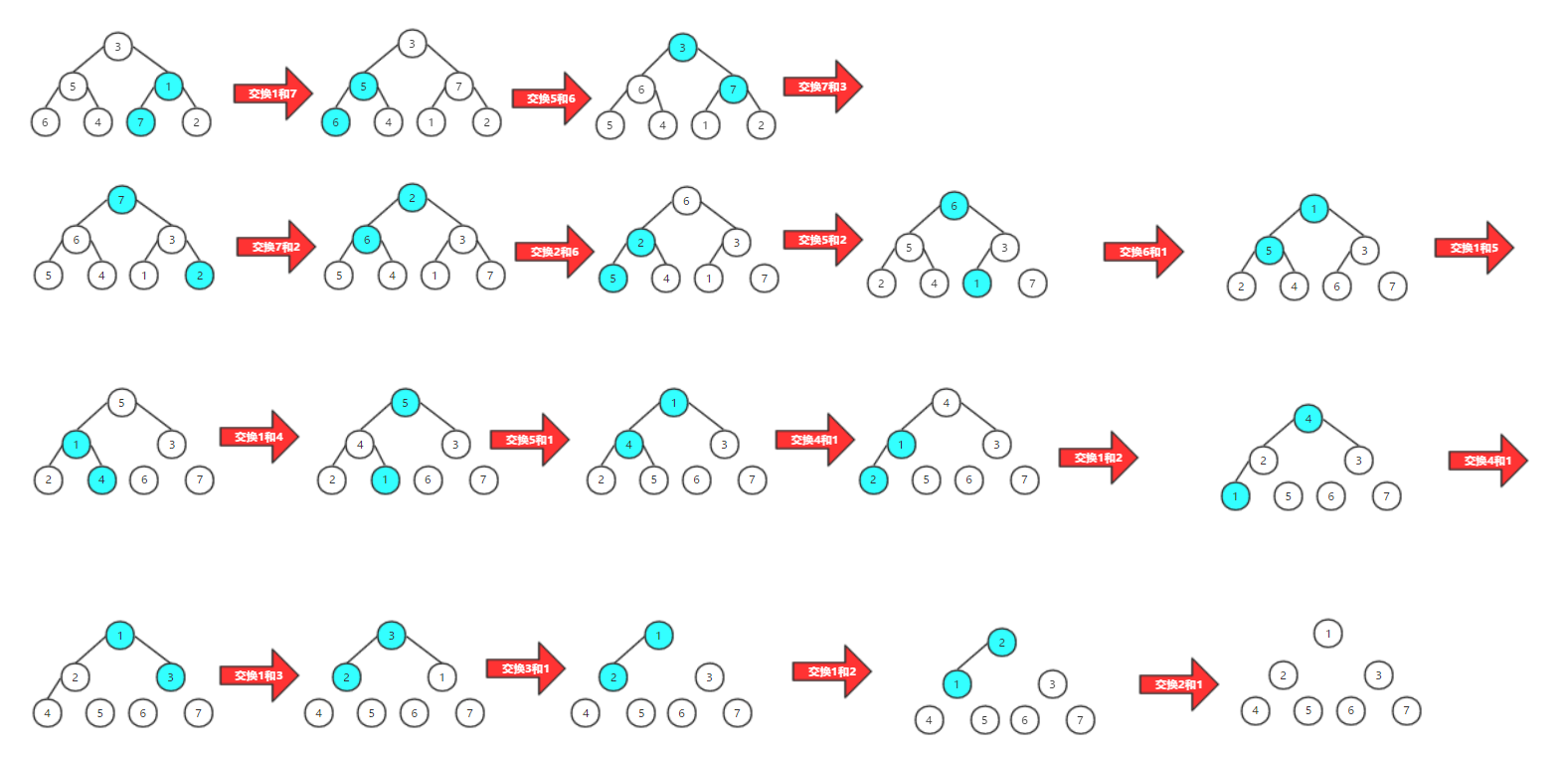
　　图片要结合代码一起看，不然看不懂的噢.......还有，这个图你最好放大了看，不然累眼睛。。。

　　最后，其实有关于排序算法还有很多，比如计数排序，桶排序，基数排序等等等等等。排序算法远不止如此。但是本系列不会介绍这么多的算法，如果你想要更深入的去了解其它算法的内容，可以自行查找相关的资料。

　　好了，终于要结束了，希望本文的内容能带给你一点点的收获。

　　最后，由于本人水平有限，能力与大神仍相差甚远，若有错误或不明之处，还望大家不吝赐教指正。非常感谢！