第六章——决策树（Decision Trees）

决策树是强大的，多功能的机器学习算法。

6.1 训练和可视化一个决策树

在iris数据集训练DecisionTreeClassifier：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X, y)

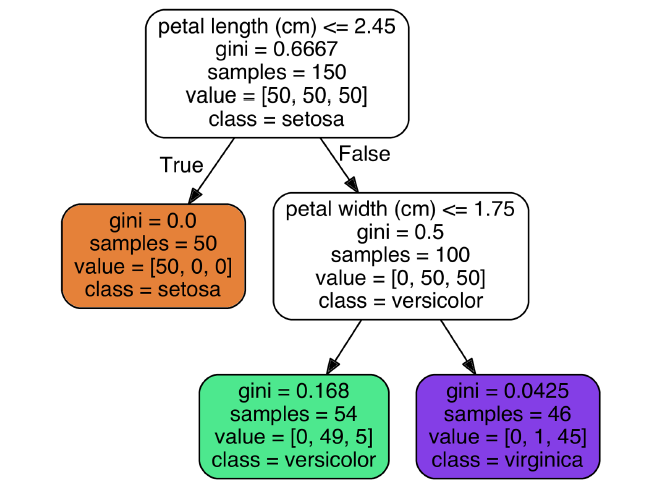
可以将训练好的决策树打印出来：

6.2 预测

从根节点开始，如果满足条件，则转向左子树，否则转向又子树。最终到达的叶子节点即为预测值。

决策树的一个优点是几乎不需要数据预处理，特别是不需要feature scaling或者centering。

基尼系数表示节点的纯洁度。如果gini=0，说明该节点是纯粹的，只包含一种类别。

第$i$个节点的Gini impurity：

$G_i = 1 - \sum_{k=1}^{n} p_{i,k}^2$

其中，$p_{i,k}$是类别$k$的样本数在节点$i$中样本总数所占的比例。

Scikit-Learn使用的是CART算法，产生的是二叉树：非叶子节点只有两个子节点。其它算法比如ID3可以生产具有更多子节点的决策树。

模型解释：白盒 Vs 黑盒：

决策树的可解释性很强，这被称作白盒模型。相应的，随机森林或者神经网络是黑盒模型。

6.3 评估类别概率（Estimating Class Probabilities）

类别的预测概率，就是叶子节点中该类别所占的比例。　　

6.4 CART训练算法

Scikit-Learn使用分类回归树（Classification And Regression Tree，CART）算法训练决策树。其思想很简单：使用属性$k$和相应的阈值$t_k$将训练集分为两个子集。搜索合适的$(k, t_k)$使得子集的纯净度最高。损失函数如下：

$J(k,t_k) = \frac{m_{left}}{m}G_{left} + \frac{m_{right}}{m}G_{right}$

其中，$G_{left}$、$G_{right}$是左、右子树的纯净度，$m_{left}$、$m_{right}$是左、右子树的样本数。

将训练集切分之后，会对子集继续切分，这是一个递归过程。如果达到最大深度就会停止（通过max_depth超参数控制），或者已经找不到可以增大纯净度的切分（比如已经完全纯净）。还有一些控制切分停止的超参数：min_samples_split, min_samples_leaf,min_weight_fraction_leaf, and max_leaf_nodes。

这是一个贪心算法，虽不能达到最优，但可以得到一足够优的结果。找到最优树属于NP完全（NP-Complete）问题，需要O(exp(m))时间，这使得即使是很小的训练集也难以求解。

6.5 计算复杂度

决策树预测过程，需要从根节点到达一个叶子节点，决策树一般是近似平衡的，这一过程复杂度为$O(log_2(m))$，与样本数无关。

训练过程需要比较所有的特征，训练复杂度是$(n times m log(m))$。

6.6 基尼系数还是熵（Gini Impurity or Entropy）？

熵：

$H_i = \sum_{k=1}^{n} p_{i,k}\ log(p_{i,k})$

二者差别不大，通常会得到相似的决策树。Gini impurity计算起来更快，所有它是默认的。如果非要说它们的区别，Gini impurity倾向于将最频繁的类别分在同一个分支，entropy倾向于生成更平衡的树。

6.7 正则化超参数（Regularization Hyperparameters）

决策树对训练数据几乎不做假设（与之相反，详细模型明显假设数据是线性的）。如果不进行约束，很容易造成过拟合。这种模型被称作无参数模型（nonparametric model），这并不是真的没有参数（通常有很多参数），而是参数个数不需要在训练之前确定下来，这就有很高的自由度去拟合训练数据。与之相反，比如线性模型这种参数模型，需要提前确定参数个数，所以其自由度是受限的，减少了过拟合的风险（但是增加了欠拟合的风险）。

为避免过拟合，需要在训练时现在决策树的自由度，这被称作正则化。正则化超参数跟算法有关，但一般情况下至少可以限制决策树的最大深度。在Scikit-Learn中这由max_depth超参数控制。

另外还有一些算法，不设限地训练决策树，训练完成后会修剪不必要的节点。如果一个节点的子节点都是叶子节点，对该节点的拆分带来的纯净度提升并不是统计学上有效的（statistically significant），那么其子节点就被认为是不必要的，会被删除掉。

6.7 回归

CART回归损失函数：

$J(k, t_k) = \frac{m_{left}}{m} MSE_{left} + \frac{m_{right}}{m} MSE_{right}$

其中，

$MSE_{node} = \sum_{i \in node}(\hat{y}_{node} - y_{(i)})^2$

$\hat{y}_{node} = \frac{1}{m_{node}}\sum_{i \in node}y^{(i)}$

6.8 不稳定性（Instability）

决策树虽然功能强大，但也有一些局限性。首先，决策树的决策边界都是正交直线（所有的切分都和某一个坐标轴垂直），这使得它们对数据集的旋转很敏感。例如，下图显示了简单的线性可分数据集，在左侧，决策树很容易将其切分。但是在右侧，数据集旋转45°，决策树出现了不必要的绕弯弯。尽管二者都很好地拟合了训练集，很明显右侧的模型难以很好地一般化。一个解决方案是使用PCA，它可以使训练集旋转到最好的方向。

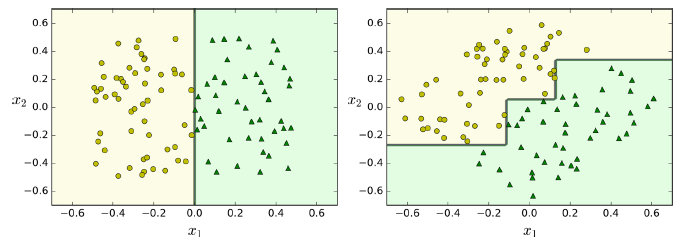
此外，决策树对训练数据集微小的变动也会很敏感。

随机森林通过许多决策树的预测平均值，可以避免这一不稳定性。