Calculating Stereo Pairs

Calculating Stereo Pairs

Written by Paul Bourke
July 1999

Introduction

The following discusses computer based generation of stereo pairs as used to create a perception of depth. Such depth perception can be useful in many fields, for example, scientific visualisation, entertainment, games, appreciation of architectural spaces, etc.

Depth cues

There are a number of cues that the human visual system uses that result in a perception of depth. Some of these are present even in two dimensional images, for example:

• Perspective.
  Objects get smaller the further away they are and parallel line converge in distance.
• Sizes of known objects.
  We expect certain object to be smaller than others. If an elephant and a tea cup appear the same size then we expect the elephant to be further away.
• Detail.
  Close objects appear in more detail, distant objects less.
• Occlusion.
  An object that blocks another is assumed to be in the foreground.
• Lighting, shadows.
  Closer objects are brighter, distant ones dimmer. There a number of other more subtle cues implied by lighting, the way a curved surface reflects light suggests the rate of curvature, shadows are a form of occlusion.
• Relative motion.
  Objects further away seem to move more slowly than objects in the foreground.

There are other cues that are not present in 2D images, they are:

• Binocular disparity.
  This is the difference in the images projected onto the back the eye (and then onto the visual cortex) because the eyes are separated horizontally by the interocular distance.
• Accommodation.
  This is the muscle tension needed to change the focal length of the eye lens in order to focus at a particular depth.
• Convergence.
  This is the muscle tension required to rotate each eye so that it is facing the focal point.

While binocular disparity is considered the dominant depth cue in most people, if the other cues are presented incorrectly they can have a strong detrimental effect. In order to render a stereo pair one needs to create two images, one for each eye in such a way that when independently viewed they will present an acceptable image to the visual cortex and it will fuse the images and extract the depth information as it does in normal viewing. If stereo pairs are created with a conflict of depth cues then one of a number of things may occur: one cue may become dominant and it may not be the correct/intended one, the depth perception will be exaggerated or reduced, the image will be uncomfortable to watch, the stereo pairs may not fuse at all and the viewer will see two separate images.

Stereographics using stereo pairs is only one of the major stereo3D dimensional display technologies, others include holographic and lenticular (barrier strip) systems both of which are autostereoscopic. Stereo pairs create a "virtual" three dimensional image, binocular disparity and convergence cues are correct but accommodation cues are inconsistent because each eye is looking at a flat image. The visual system will tolerate this conflicting accommodation to a certain extent, the classical measure is normally quoted as a maximum separation on the display of 1/30 of the distance of the viewer to the display.

The case where the object is behind the projection plane is illustrated below. The projection for the left eye is on the left and the projection for the right eye is on the right, the distance between the left and right eye projections is called the horizontal parallax. Since the projections are on the same side as the respective eyes, it is called a positive parallax. Note that the maximum positive parallax occurs when the object is at infinity, at this point the horizontal parallax is equal to the interocular distance.

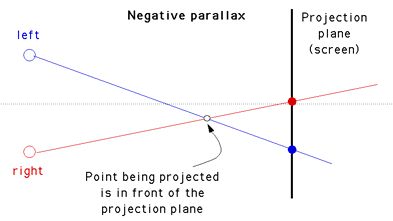
If an object is located in front of the projection plane then the projection for the left eye is on the right and the projection for the right eye is on the left. This is known as negative horizontal parallax. Note that a negative horizontal parallax equal to the interocular distance occurs when the object is half way between the projection plane and the center of the eyes. As the object moves closer to the viewer the negative horizontal parallax increases to infinity.

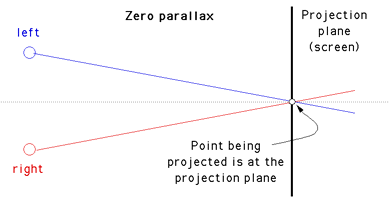
If an object lies at the projection plane then its projection onto the focal plane is coincident for both the left and right eye, hence zero parallax.

Rendering

There are a couple of methods of setting up a virtual camera and rendering two stereo pairs, many methods are strictly incorrect since they introduce vertical parallax. An example of this is called the "Toe-in" method, while incorrect it is still often used because the correct "off axis" method requires features not always supported by rendering packages. Toe-in is usually identical to methods that involve a rotation of the scene. The toe-in method is still popular for the lower cost filming because offset cameras are uncommon and it is easier than using parallel cameras which requires a subsequent trimming of the stereo pairs.

Toe-in (Incorrect)

In this projection the camera has a fixed and symmetric aperture, each camera is pointed at a single focal point. Images created using the "toe-in" method will still appear stereoscopic but the vertical parallax it introduces will cause increased discomfort levels. The introduced vertical parallax increases out from the center of the projection plane and is more important as the camera aperture increases.

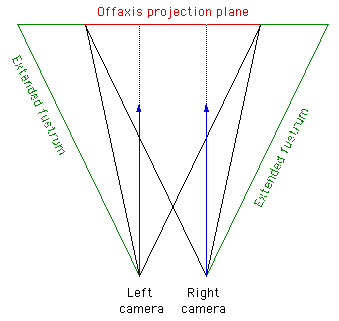
Off-axis (Correct)

This is the correct way to create stereo pairs. It introduces no vertical parallax and is therefore creates the less stressful stereo pairs. Note that it requires a non symmetric camera frustum, this is supported by some rendering packages, in particular, OpenGL.

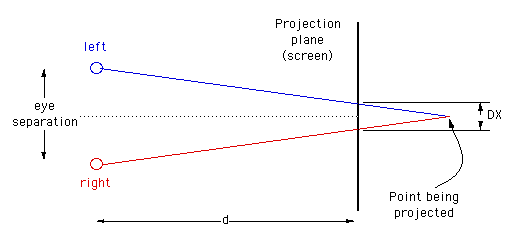
Objects that lie in front of the projection plane will appear to be in front of the computer screen, objects that are behind the projection plane will appear to be "into" the screen. It is generally easier to view stereo pairs of objects that recede into the screen, to achieve this one would place the focal point closer to the camera than the objects of interest. Note, this doesn't lead to as dramatic an effect as objects that pop out of the screen.

The degree of the stereo effect depends on both the distance of the camera to the projection plane and the separation of the left and right camera. Too large a separation can be hard to resolve and is known as hyperstereo. A good ballpark separation of the cameras is 1/20 of the distance to the projection plane, this is generally the maximum separation for comfortable viewing. Another constraint in general practice is to ensure the negative parallax (projection plane behind the object) does not exceed the eye separation.

A common measure is the parallax angle defined as thea = 2 atan(DX / 2d) where DX is the horizontal separation of a projected point between the two eyes and d is the distance of the eye from the projection plane. For easy fusing by the majority of people, the absolute value of theta should not exceed 1.5 degrees for all points in the scene. Note theta is positive for points behind the scene and negative for points in front of the screen. It is not uncommon to restrict the negative value of theta to some value closer to zero since negative parallax is more difficult to fuse especially when objects cut the boundary of the projection plane.

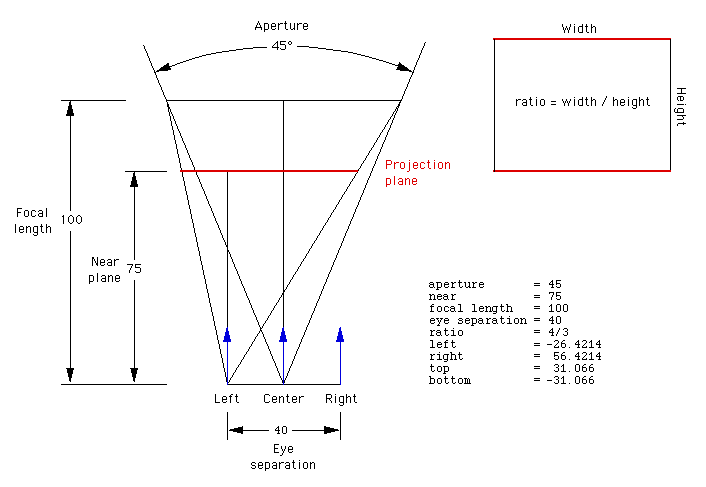
Rule of thumb for rendering software

Getting started with ones first stereo rendering can be a hit and miss affair, the following approach should ensure success. First choose the camera aperture, this should match the "sweet spot" for your viewing setup, typically between 45 and 60 degrees). Next choose a focal length, the distance at which objects in the scene will appear to be at zero parallax. Objects closer than this will appear in front of the screen, objects further than the focal length will appear behind the screen. How close objects can come to the camera depends somewhat on how good the projection system is but closer than half the focal length should be avoided. Finally, choose the eye separation to be 1/30 of the focal length.

References

Bailey, M, Clark D
Using ChromaDepth to Obtain Inexpensive Single-image Stereovision for Scientific Visualisation
Journal of Graphics Tools, ACM, Vol 3 No 3 pp1-9

Baker, J.
Generating images for a time multiplexed stereoscopic computer graphics system.
True 3D imaging techniques and display technologies
McAllister, D.F. and Robbins, W.E. (Editors)
SPIE Proc 761, 1987.

Bos, P. et al
High performance 3D viewing system using passive glasses
1988 SID Digest of technical papers, vol 19

Bos, P. et al
A liquid crystal optical switching device (pi cell)
1983 SID Digest of technical papers, vol 15

Grotch, S.L.
Three dimensional and stereoscopic graphics for scientific data display and analysis
IEEE Computer Graphics and Applications 3,8, Nov 1983, 31-34

Hodges, L.F. and McAllister, D.F.
Stereo and alternating pair techniques for display of computer generated images 
IEEE Computer Graphics and Applications 5,9, September 1985, 38-45

Lipton, L, Meyer, L
A flicker free field sequential stereoscopic video system
SMPTE Journal, November 1984, pp1047.

Lipton, L., Ackerman.,M
Liquid crystal shutter system for stereoscopic and other applications
US Patent No 4,967,268, Oct 30, 1990

Nakagawa, K., Tsubota, K., Yamamoto, K
Virtual Stereoscopic display system
US Patent No. 4,870,486, Sept 26, 1989

Roese, J.A. and McCleary, L.E.
Stereoscopic computer graphics for simulation and modeling
Proc SIGGRAPH 13, 2, 1979, 41-47

Southard, D.A
Transformations for Stereoscopic Visual Simulation
Computer and Graphics, Vol 16, No 4 pp 401-410, 1992

Course notes, #24
Stereographics
ACM SIGGRAPH, 1989

Weissman, M.
3D Measurements from Video Stereo Pairs
SPIE Three Dimensional Imaging and Remote Sensing Imaging, Vol 902, pp 85

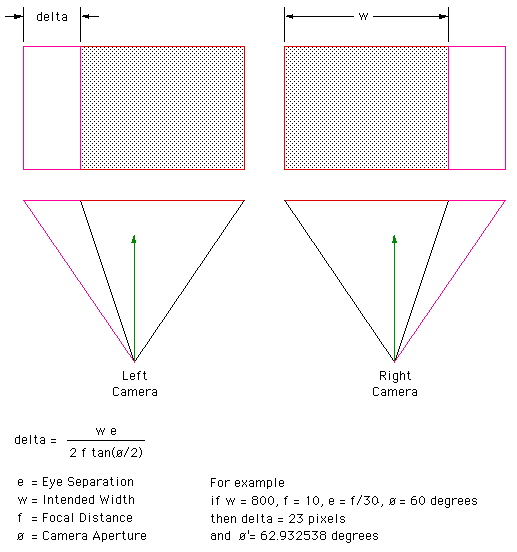
Creating correct stereo pairs from any raytracer

Written by Paul Bourke
February 2001

Contribution by Chris Gray: AutoXidMary.mcr, a camera configuration for 3DStudioMax that uses the XidMary Camera.

Introduction

Many rendering packages provide the necessary tools to create correct stereo pairs (eg: OpenGL), other packages can transform their geometry appropriately (translations and shears) so that stereo pairs can be directly created, many rendering packages only provide straightforward perspective projections. The following describes a method of creating stereo pairs using such packages. While it is possible to create stereo pairs using PovRay with shear transformations, PovRay will be used to illustrate this technique which can be applied to any rendering software that supports only perspective projections (this method is often easier than the translate/shear matrix method).

Basic idea

Creating stereo pairs involves rendering the left and right eye views from two positions separated by a chosen eye spacing. The eye (camera) looks along parallel vectors. The frustum from each eye to each corner of the projection plane is asymmetric. The solution to creating correct stereo pairs using only symmetric fristums is to extend the frustum (horizontally) for each eye (camera) making it symmetric. After rendering, those parts of the image resulting from the extended fustrum are timmed off. The camera geometry is illustrated below, the relevant details can be translated into the camera specification for your favourite rendering package.

All that remains is to calculate the amount of trimming required for a given focal length and eye separation. Since one normally has a target image width it is usual to render the image larger so that after the trim the image is the desired size. The amount of offset depends on the desired focal length, that is, the distance at which there is no vertical parallax. The amount by which the images are extended and then trimmed (working not given) is given by the following:

	e w
delta =
	2 fo tan(a / 2)

Where "w" is the image width, "fo" the focal length (zero parallax), "e" the eye separation, and "a" the intended horizontal aperture. In order to get the final aperture "a" after the image is trimmed, the actual aperture "a'" needs to be modified as follows.

	(w + delta) tan(a/2)
a' = 2 atan
	w

Note that not all rendering packages use the horizontal aperture but rather a vertical aperture eg: OpenGL. As expected as the focal length tends to infinity the amount by which the images are trimmed tends to 0, similarly as the eye separation tends to 0.

To combine the images, delta is trimmed off the left of the left image and delta pixels are trimmed off the right of the right image.

Example 1

Consider a PovRay model scene file for stereo pair rendering where the eye separation is 0.2, the focal length (zero parallax) is 3, the aperture 60 degrees, and the final image size is supposed to be 800 by 600....delta comes to 46. Example PovRay model files are given for each camera. Note that one could ask PovRay to render just the intended regions of each image by setting a start and end column.

asteroid_l.pov #declare WIDTH = 846; #declare HEIGHT = 600; #declare EYESEP = 0.2; camera { location <-EYESEP/2,0,-3> up y right WIDTH*x/HEIGHT angle 62.932538 sky <0,1,0> look_at <-EYESEP/2,0,0> } #include "material.inc" #include "lighting.inc" #include "geometry.inc"

asteroid_r.pov #declare WIDTH = 846; #declare HEIGHT = 600; #declare EYESEP = 0.2; camera { location <EYESEP/2,0,-3> up y right WIDTH*x/HEIGHT angle 62.932538 sky <0,1,0> look_at <EYESEP/2,0,0> } #include "material.inc" #include "lighting.inc" #include "geometry.inc"

Example 2

Creating stereoscopic images that are easy on the eyes

Written by Paul Bourke
February 2003

There are some unique considerations when creating effective stereoscopic images whether as still images, interactive environments, or animations/movies. In the discussion of these given below it will be assumed that the correct stereopairs have been created, that is, perspective projection with parallel cameras resulting is the so called offaxis projection. It should be noted that not all of these are hard and fast rules and they may be inherent in the type of image content being created.

• Ghosting

  Stereoscopic projection is never perfect, that is, there is some leakage of the left eye image into the right eye and visa-versa. Being aware of the degree of ghosting in the particular system being used and limiting the parallax so that the human visual system doesn't reject the pairs as belonging to the one object is critical. The most common limitation this places on the content is how close objects can be brought to the viewer, it is this negative parallax region where the separation can go to infinity (compared to objects in positive parallax, behind the plane, where the separation is at most the same as the eye separation in world coordinates).

• High contrast

  Ghosting is most obvious in regions of high contrast. This isn't usually an issue for filmed or photorealistic computer generated images but is very common in cartoon or visualisation applications. It is common in these applications to have a black background say, the simplest solution is often simply to use a grey background. Of course this isn't always desirable since it may impact on the subject matter, for example, stars on the blackness of outer space. Be aware that the degree of ghosting varies between people, the level of separation that can be supported should be tested by using a range of people.

• Screen border

  Objects in the negative parallax region (in front of the screen) will present conflicting cues to the visual system if they are cut by the border of screen, a region that is clearly at zero parallax. This is the primary reason why individual objects can be brought out in front of the screen while larger objects (eg: buildings) that cannot be contained need to be behind the screen (positive parallax). Of course this is most serious on a single stereo wall and less of a problem on wider displays. For example, in the image below on the right it would be possible to bring the planet in front of the screen while in the situation on the right it would be significantly less effective.

• Occlusion by other audience members

  The effect of the line of site being blocked by other members of the audience can lead to conflicting cue if the blocking object is at similar or greater depths than the stereo content. For this reason it is normally more important for stereoscopic theatres to have included seating compared to traditional theatres.

• Motion cues

  After parallax motion cues are perhaps the next strongest cue for depth perception even stronger perhaps than occlusion. It is usually easily noticeable that the depth perception is enhanced when objects at different depths are moving with respect to the viewer. This can be put to good use during preview and evaluation stages of a production, if a still frame from an animated sequence has good depth cues then it will be even better when the scene is animated.

• Vertical structure

  The parallax information requires vertical structure. For example, a plane with a constant colour will not convey nearly the same sense of depth than one with a textured surface.

  

  Similarly horizontal lines don't contain much parallax information. In the case of stereoscopic illustration or visualisation it is therefore common to use dashed lines (for example on the right below) rather than the solid line on the left.

  

  At other times it isn't so easy to introduce vertical parallax, one obvious example is the presentation of fuzzy/blurred objects such as clouds. As a result these often don't convey a strong sense of depth by themselves.

  

• Parallax/structure interference

  It is possible for the frequency of geometry or texture detail to exactly match the parallax separation, this can lead to disturbing ambiguous images and increased eyestrain. For example, in the scene below what if the parallax separation of the vertical red lines matched the spacing of the lines. In that case how does the visual system choose to interpret the depth as from the actual parallax or the equally valid 0 parallax.

  

  Such ambiguous cases are normally naturally resolved by the parallax of the surrounding geometry. However, this isn't always the case for synthetic or data visualisation based renderings.

• Noisy Texture

  Noisy textures on surfaces will result in poor depth perception if the frequency is so high that there effectively isn't matching visual information between the stereo pairs. For example, the image below on the left would have matching structure between two stereo pairs while the one on the right probably wouldn't. This is similar to high frequency textures "shimmering" in animation sequences, it can be helped by high levels of antialiasing but never completely cured.

• Mirror reflections

  Correctly generated reflections will work correctly in stereo pairs. However many packages support features which mean that the reflections are not correct but only approximations, while this isn't normally an issue in non-stereo it can give very disturbing results in stereo. Two cases where this can arise are when perturbed normals are used to create surface texture or when normals are used to give simple faceted geometry the appearance of being smooth. In either case the reflections are often based upon the underlying geometry which is different to the perceived geometry (perturbed or smoothed by surface normals).... the result is conflicting reflections between the stereo pairs.

• Specular hilights

  It is possible, usually in rendered content, for a specular hilight to result in a bright hilight in one eye and not the other. This is because the model for specular takes into account the relative angle between the light AND the camera, unlike diffuse reflection that is only a function of the light position and the surface normal. This can also occur simply with highly reflective surfaces.

  

• Positive parallax

  Positive parallax (objects behind the screen) is in general easier to look at and minimises eye strain.

• Focal distance changes

  Frequent cuts in stereo movie/animation forces the viewer to adjust to the different focal lengths. Frequent cuts to scene with very different content and focal length will quickly introduce stress on the visual system.

3D Stereo Rendering 
Using OpenGL (and GLUT)

Source code for the incorrect (but close) "Toe-in" stereo,
and the correct Offaxis stereo

Written by Paul Bourke
November 1999
Updated May 2002

Introduction

The following is intended to get someone started creating 3D stereo applications using OpenGL and the associated GLUT library. It is assumed that the reader is both familiar with how to create the appropriate eye positions for comfortable stereo viewing (see link in the title of the page) and the reader has an OpenGL card (or software implementation) and any associated hardware (eg: glasses) needed to support stereo graphic viewing.

The description of the code presented here will concentrate on the stereo aspects, the example does however create a real, time varying OpenGL object, namely the pulsar model shown on the right. The example also contains examples of mouse and keyboard controls of the camera position. The example is not intended to illustrate more advanced OpenGL techniques and indeed it does not do things particularly efficiently, in particular it should, but does not, use display lists. The example does not use textures as that is a large separate topic and would only confuse the task at hand.

Conventions

The example code conforms to a couple of local conventions. The first is that it can be run in a window or full screen (arcade game) mode. By convention the application runs in a window unless the "-f" command line option is specified. Full screen mode is supported in the most recent versions of the GLUT library. The decision to use full screen mode is made with the following snippet.

   glutCreateWindow("Pulsar model");
   glutReshapeWindow(600,400);
   if (fullscreen)
      glutFullScreen();

It is also useful to be able to run the application in stereo mode or mono mode, the convention is to run in mono unless the command line switch "-s" is supplied. The full usage help information in the example presented here is available by running the application with the "-h" command line option, for example:

>pulsar -h
Usage: pulsar [-h] [-f] [-s] [-c]
          -h   this text
          -f   full screen
          -s   stereo
          -c   show construction lines
Key Strokes
  arrow keys   rotate left/right/up/down
  left mouse   rotate
middle mouse   roll
           c   toggle construction lines
           i   translate up
           k   translate down
           j   translate left
           l   translate right
           [   roll clockwise
           ]   roll anti clockwise
           q   quit

Stereo

The first thing that needs to be done to support stereo is to initialise the GLUT library for stereo operation. If your card/driver combination don't support stereo this will fail.

   glutInit(&argc,argv);
   if (!stereo)
      glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);
   else
      glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH | GLUT_STEREO);

In stereo mode this defines two buffers namely GL_BACK_LEFT and GL_BACK_RIGHT. The appropriate buffer is selected before operations that would affect it are performed, this is using the routine glDrawBuffer(). So for example to clear the two buffers:

   glDrawBuffer(GL_BACK_LEFT);
   glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
   if (stereo) {
      glDrawBuffer(GL_BACK_RIGHT);
      glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
   }

Note that some cards are optimised to clear both left and right buffers if GL_BACK is cleared, this can be significantly faster. In these cases one clears the buffers as follows.

   glDrawBuffer(GL_BACK);
   glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

Projection

All that's left now is to render the geometry into the appropriate buffer. There are many ways this can be organised depending on the way the particular application is written, in this example see the Display() handler. Essentially the idea is to select the appropriate buffer and render the scene with the appropriate projection.

Toe-in Method A common approach is the so called "toe-in" method where the camera for the left and right eye is pointed towards a single focal point and gluPerspective() is used.

   glMatrixMode(GL_PROJECTION);
   glLoadIdentity();
   gluPerspective(camera.aperture,screenwidth/(double)screenheight,0.1,10000.0);

   if (stereo) {

      CROSSPROD(camera.vd,camera.vu,right);
      Normalise(&right);
      right.x *= camera.eyesep / 2.0;
      right.y *= camera.eyesep / 2.0;
      right.z *= camera.eyesep / 2.0;

      glMatrixMode(GL_MODELVIEW);
      glDrawBuffer(GL_BACK_RIGHT);
      glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
      glLoadIdentity();
      gluLookAt(camera.vp.x + right.x,
                camera.vp.y + right.y,
                camera.vp.z + right.z,
                focus.x,focus.y,focus.z,
                camera.vu.x,camera.vu.y,camera.vu.z);
      MakeLighting();
      MakeGeometry();

      glMatrixMode(GL_MODELVIEW);
      glDrawBuffer(GL_BACK_LEFT);
      glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
      glLoadIdentity();
      gluLookAt(camera.vp.x - right.x,
                camera.vp.y - right.y,
                camera.vp.z - right.z,
                focus.x,focus.y,focus.z,
                camera.vu.x,camera.vu.y,camera.vu.z);
      MakeLighting();
      MakeGeometry();

   } else {

      glMatrixMode(GL_MODELVIEW);
      glDrawBuffer(GL_BACK);
      glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
      glLoadIdentity();
      gluLookAt(camera.vp.x,
                camera.vp.y,
                camera.vp.z,
                focus.x,focus.y,focus.z,
                camera.vu.x,camera.vu.y,camera.vu.z);
      MakeLighting();
      MakeGeometry();
   }

   /* glFlush(); This isn't necessary for double buffers */
   glutSwapBuffers();

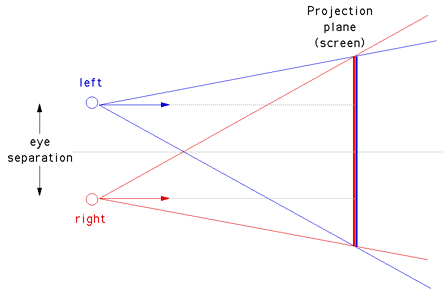
Correct method The Toe-in method while giving workable stereo pairs is not correct, it also introduces vertical parallax which is most noticeable for objects in the outer field of view. The correct method is to use what is sometimes known as the "parallel axis asymmetric frustum perspective projection". In this case the view vectors for each camera remain parallel and a glFrustum() is used to describe the perspective projection.

   /* Misc stuff */
   ratio  = camera.screenwidth / (double)camera.screenheight;
   radians = DTOR * camera.aperture / 2;
   wd2     = near * tan(radians);
   ndfl    = near / camera.focallength;

   if (stereo) {

      /* Derive the two eye positions */
      CROSSPROD(camera.vd,camera.vu,r);
      Normalise(&r);
      r.x *= camera.eyesep / 2.0;
      r.y *= camera.eyesep / 2.0;
      r.z *= camera.eyesep / 2.0;

      glMatrixMode(GL_PROJECTION);
      glLoadIdentity();
      left  = - ratio * wd2 - 0.5 * camera.eyesep * ndfl;
      right =   ratio * wd2 - 0.5 * camera.eyesep * ndfl;
      top    =   wd2;
      bottom = - wd2;
      glFrustum(left,right,bottom,top,near,far);

      glMatrixMode(GL_MODELVIEW);
      glDrawBuffer(GL_BACK_RIGHT);
      glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
      glLoadIdentity();
      gluLookAt(camera.vp.x + r.x,camera.vp.y + r.y,camera.vp.z + r.z,
                camera.vp.x + r.x + camera.vd.x,
                camera.vp.y + r.y + camera.vd.y,
                camera.vp.z + r.z + camera.vd.z,
                camera.vu.x,camera.vu.y,camera.vu.z);
      MakeLighting();
      MakeGeometry();

      glMatrixMode(GL_PROJECTION);
      glLoadIdentity();
      left  = - ratio * wd2 + 0.5 * camera.eyesep * ndfl;
      right =   ratio * wd2 + 0.5 * camera.eyesep * ndfl;
      top    =   wd2;
      bottom = - wd2;
      glFrustum(left,right,bottom,top,near,far);

      glMatrixMode(GL_MODELVIEW);
      glDrawBuffer(GL_BACK_LEFT);
      glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
      glLoadIdentity();
      gluLookAt(camera.vp.x - r.x,camera.vp.y - r.y,camera.vp.z - r.z,
                camera.vp.x - r.x + camera.vd.x,
                camera.vp.y - r.y + camera.vd.y,
                camera.vp.z - r.z + camera.vd.z,
                camera.vu.x,camera.vu.y,camera.vu.z);
      MakeLighting();
      MakeGeometry();

   } else {

      glMatrixMode(GL_PROJECTION);
      glLoadIdentity();
      left  = - ratio * wd2;
      right =   ratio * wd2;
      top    =   wd2;
      bottom = - wd2;
      glFrustum(left,right,bottom,top,near,far);

      glMatrixMode(GL_MODELVIEW);
      glDrawBuffer(GL_BACK);
      glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
      glLoadIdentity();
      gluLookAt(camera.vp.x,camera.vp.y,camera.vp.z,
                camera.vp.x + camera.vd.x,
                camera.vp.y + camera.vd.y,
                camera.vp.z + camera.vd.z,
                camera.vu.x,camera.vu.y,camera.vu.z);
      MakeLighting();
      MakeGeometry();
   }

   /* glFlush(); This isn't necessary for double buffers */
   glutSwapBuffers();

Note that sometimes it is appropriate to use the left eye position when not in stereo mode in which case the above code can be simplified. It seems more elegant and consistent when moving between mono and stereo if the point between the eyes is used when in mono.

On the off chance that you want to write the code differently and would like to test the correctness of the glFrustum() parameters, here's an explicit example.

Passive stereo

Updated in May 2002: sample code to deal with passive stereo, that is, drawing the left eye to the left half of a dual display OpenGL card and the right eye to the right half. pulsar2.c and pulsar2.h

Macintosh OS-X example

Source code and Makefile illustrating stereo under Mac OS-X using "blue line" syncing, contributed by Jamie Cate.

Demonstration stereo application for Mac OS-X from the Apple development site based upon the method and code described above: GLUTStereo. (Also uses blue line syncing)

Python Example contributed by Peter Roesch
python.zip

Cross-eye stereo modification contributed by Todd Marshall
pulsar_cross.c

Offaxis frustums - OpenGL

Written by Paul Bourke
July 2007

The following describes one (there are are a number of alternatives) system for create perspective offset frustums for stereoscopic projection using OpenGL. This is convenient for non observer tracked viewing on a single stereoscopic panel in these cases there is no clear relationship between the model dimensions and the screen. Note that for multiwall immersive displays the following is not the best approach, the appropriate method requires a knowledge of the screen geometry and the observer position and generally the model is scaled into real world coordinates.

Camera is defined by its position, view direction, up vector, eye separation, distance to zero parallax (see fo below) and the near and far cutting planes. Position, eye separation, zero parallax distance, and cutting planes are most conveniently specified in model coordinates, direction and up vector are orthonormal vectors. With regard to parameters for adjusting stereoscopic viewing I would argue that the distance to zero parallax is the most natural, not only does it relate directly to the scale of the model and the relative position of the camera, it also has a direct bearing on the stereoscopic result ... namely that objects at that distance will appear to be at the depth of the screen. In order not to burden the operators with multiple stereo controls one can usually just internally set the eye separation to 1/30 of the zero parallax distance (camera.eyesep = camera.fo / 30), this will give acceptable stereoscopic viewing in almost all situations and is independent of model scale.

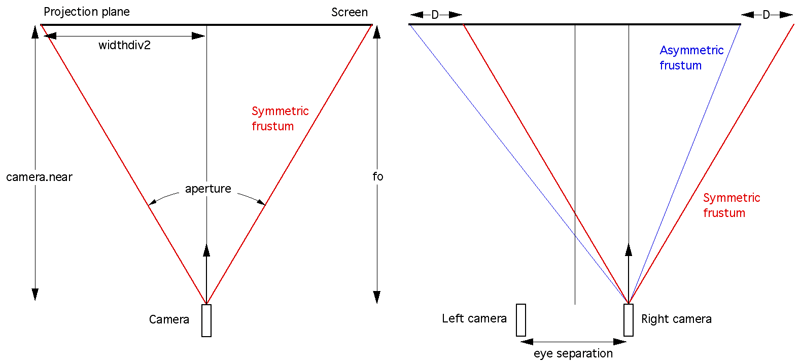
The above diagram (view from above the two cameras) is intended to illustrate how the amount by which to offset the frustums is calculated. Note there is only horizontal parallax. This is intended to be a guide for OpenGL programmers, as such there are some assumptions that relate to OpenGL that may not be appropriate to other APIs. The eye separation is exaggerated in order to make the diagram clearer.

The half width on the projection plane is given by

widthdiv2 = camera.near * tan(camera.aperture/2)

This is related to world coordinates by similar triangles, the amount D by which to offset the view frustum horizontally is given by

D = 0.5 * camera.eyesep * camera.near / camera.fo

aspectratio = windowwidth / (double)windowheight;         // Divide by 2 for side-by-side stereo
widthdiv2   = camera.near * tan(camera.aperture / 2); // aperture in radians
cameraright = crossproduct(camera.dir,camera.up);         // Each unit vectors
right.x *= camera.eyesep / 2.0;
right.y *= camera.eyesep / 2.0;
right.z *= camera.eyesep / 2.0;

Symmetric - non stereo camera

   glMatrixMode(GL_PROJECTION);
   glLoadIdentity();
   glViewport(0,0,windowwidth,windowheight);
   top    =   widthdiv2;
   bottom = - widthdiv2;
   left   = - aspectratio * widthdiv2;
   right  =   aspectratio * widthdiv2;
   glFrustum(left,right,bottom,top,camera.near,camera.far);
   glMatrixMode(GL_MODELVIEW);
   glLoadIdentity();
   gluLookAt(camera.pos.x,camera.pos.y,camera.pos.z,
             camera.pos.x + camera.dir.x,
             camera.pos.y + camera.dir.y,
             camera.pos.z + camera.dir.z,
             camera.up.x,camera.up.y,camera.up.z);
   // Create geometry here in convenient model coordinates

Asymmetric frustum - stereoscopic

   // Right eye
   glMatrixMode(GL_PROJECTION);
   glLoadIdentity();
   // For frame sequential, earlier use glDrawBuffer(GL_BACK_RIGHT);
   glViewport(0,0,windowwidth,windowheight);
   // For side by side stereo
   //glViewport(windowwidth/2,0,windowwidth/2,windowheight);
   top    =   widthdiv2;
   bottom = - widthdiv2;
   left   = - aspectratio * widthdiv2 - 0.5 * camera.eyesep * camera.near / camera.fo;
   right  =   aspectratio * widthdiv2 - 0.5 * camera.eyesep * camera.near / camera.fo;
   glFrustum(left,right,bottom,top,camera.near,camera.far);
   glMatrixMode(GL_MODELVIEW);
   glLoadIdentity();
   gluLookAt(camera.pos.x + right.x,camera.pos.y + right.y,camera.pos.z + right.z,
             camera.pos.x + right.x + camera.dir.x,
             camera.pos.y + right.y + camera.dir.y,
             camera.pos.z + right.z + camera.dir.z,
             camera.up.x,camera.up.y,camera.up.z);
   // Create geometry here in convenient model coordinates

   // Left eye
   glMatrixMode(GL_PROJECTION);
   glLoadIdentity();
   // For frame sequential, earlier use glDrawBuffer(GL_BACK_LEFT);
   glViewport(0,0,windowwidth,windowheight);
   // For side by side stereo
   //glViewport(0,0,windowidth/2,windowheight);
   top    =   widthdiv2;
   bottom = - widthdiv2;
   left   = - aspectratio * widthdiv2 + 0.5 * camera.eyesep * camera.near / camera.fo;
   right  =   aspectratio * widthdiv2 + 0.5 * camera.eyesep * camera.near / camera.fo;
   glFrustum(left,right,bottom,top,camera.near,camera.far);
   glMatrixMode(GL_MODELVIEW);
   glLoadIdentity();
   gluLookAt(camera.pos.x - right.x,camera.pos.y - right.y,camera.pos.z - right.z,
             camera.pos.x - right.x + camera.dir.x,
             camera.pos.y - right.y + camera.dir.y,
             camera.pos.z - right.z + camera.dir.z,
             camera.up.x,camera.up.y,camera.up.z);
   // Create geometry here in convenient model coordinates

Notes

• Due to the possibility of extreme negative parallax separation as objects come closer to the camera than the zero parallax distance, it is common practice to link the near cutting plane to the zero parallax distance. The exact relationship depends on the degree of ghosting of the projection system but camera.near = camera.fo / 5 is usually appropriate.

• When the camera is adjusted, for example during a flight path, it is important to ensure the direction and up vectors remain orthonormal. This follows naturally when using quaternions and there are ways of ensuring this when using other systems for camera navigation.

• Developers are encouraged to support both side-by-side stereo as well as frame sequential (also called quad buffer stereo). The only difference is the viewport parameters, setting the drawing buffer to either the back buffer or the left/right back buffers, and when to clear the back buffer(s).

• The camera aperture above is the horizontal field of view not the more usual vertical field of view that is more conventional in OpenGL. Most end users think in terms of horizontal FOV than vertical FOV.