【NLP】蓦然回首：谈谈学习模型的评估系列文章（一）

统计角度窥视模型概念

作者：白宁超

2016年7月18日17:18:43

摘要：写本文的初衷源于基于HMM模型序列标注的一个实验，实验完成之后，迫切想知道采用的序列标注模型的好坏，有哪些指标可以度量。于是，就产生了对这一专题进度学习总结，这样也便于其他人参考，节约大家的时间。本文依旧旨在简明扼要梳理出模型评估核心指标，重点达到实用。本文布局如下：第一章采用统计学习角度介绍什么是学习模型以及如何选择，因为现今的自然语言处理方面大都采用概率统计完成的，事实证明这也比规则的方法好。第二章采用基于数据挖掘的角度探讨模型评估指标和选择。第三章采用统计自然语言处理的方法看看模型评价方法。第四章以R语言为实例，进行实战操作，更深入了解模型的相关问题。（本文原创，转载请注明出处：统计角度窥视模型概念。)

目录

---

【自然语言处理：谈谈学习模型的评估（一）】：统计角度窥视模型概念

【自然语言处理：谈谈学习模型的评估（二）】：基于Data Mining角度的模型评估与选择

【自然语言处理：谈谈学习模型的评估（三）】：基于NLP角度的模型评价方法

【自然语言处理：谈谈学习模型的评估（四）】：基于R语言的模型案例实战

1 什么是模型？

---

1.1  概念简述

李航《统计学习方法》一书：统计学习方法是由模型、策略和算法构成的，即统计学习方法的三要素构成，简化：方法=模型+策略+算法

维基百科对数学模型描述：数学模型是对所描述的对象用数学语言所作出的描述和处理。

百度百科对策略描述：策略是学习是一项复杂的智能活动，学习过程与推理过程是紧密相连的，按照学习中使用推理的多少，机器学习所采用的策略大体上可分为4种——机械学习、通过传授学习、类比学习和通过事例学习。学习中所用的推理越多，系统的能力越强。

单纯定义看，不免让人一头雾水，究竟何为模型？还是没有明确的概念，下文将以数学描述+形式化阐述这个问题。首先解决了什么是模型，咱们才能进行模型好坏指标的评价，进而选择适合的学习模型。

模型：所有学习的条件概率分布或者决策函数。

模型的假设空间：包含所有有可能的条件概率分布或者决策函数。

1.2 实例解析

假设决策函数是输入变量的线性函数，模型的假设空间就是这些线性函数构成的函数集合，假设空间中的模型一般为无穷多个。【现实应用：假设解决序列词性标注的的函数模型M，模型的假设空间的由不同参数构成的M模型。（不是很严谨，辅助理解。）】

形式化表示：假设空间F表示，假设空间可以为决策函数的集合：

x，y在输入空间X和输出空间Y上的变量，这时F通常由一个参数向量决定的函数族：

参数向量θ取值于n维欧氏空间 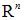，称为参数空间。

假设空间也可以定义为条件概率集合：

其中x和y是定义在输入空间X和Y上的随机变量，这时F通常是一个参数向量的决定的条件概率分布族：

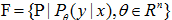
参数向量θ取值于n维欧氏空间，称为参数空间。

注意：由决策函数表示的模型为非概率模型（如上述F函数），由条件概率表示的模型为概率模型（如上述y=f(x)函数）。

2 如何进行模型评估和模型选择？

2.1  训练误差和测试误差

好的模型的特征：对已知数据和未知数据都有很好的预测能力。

学习方法评估标准：基于损失函数的模型的训练误差和测试误差为指标。

假设学习到的模型 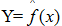 ,训练误差是模型 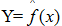关于训练数据集的平均损失：

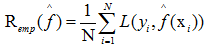
其中N是训练样本容量。

测试误差是模型 关于测试数据集的平均损失：

其中N’是训练样本容量。

2.2 实例

若损失函数是0-1损失时候（0-1损失参考具体相关知识），测试误差就变成了常见的测试数据集上的误差率。

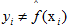，这里的I是指示函数，即 时为1，否则为0。

相应的，常见的测试数据集上的准确率是：

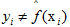，这里的I是指示函数，即 时为1，否则为0。

显然：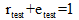

2.3 实例解析

根据误差率和准确率可知，测试误差反映了学习方法对未知情况的测试数据集的预测能力，测试误差小的方法具有很好的预测能力，更有效的预测。通常将学习方法对未知数据的预测能力称为泛化能力。

由此我们可以应用到现实想NLP模型中，诸如分类模型，当测试误差更小的时候，分类更加准确。聚类模型中，当测试误差较小时候，聚类效果更好等等。那么，在追去测试误差较小时候，就要在训练上下功夫。一味苛求训练效果好，训练误差小，以至于所选择的模型复杂度非常高，这样的低训练误差，能换回好的预测？其实这就容易出现过拟合，如何避免过拟合选择更好的模型？下节继续。

3   过拟合与模型选择

3.1 何时进行模型选择？

当假设空间含有不同的复杂度（如，不同的参数个数）的模型时，就要面临模型选择问题，以期我们所表达的模型与真实的模型（参数个数）相同或相近。

过拟合：一味追求提高对训练数据的预测能力，所选择模型的复杂度往往比真实模型高，此现象就是过拟合。

过拟合指学习时选择的模型包含的参数过多，以至于出现模型对已经数据预测的好，但是对未知数据预测能力较差。模型选择准则是避免过拟合并且去提高模型预测的能力。

3.2 实例

给出一个训练数据集 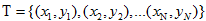 和一个M次多项式的模型

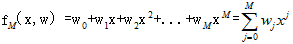
完成下面10个数据点的拟合。

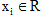是输入序列集x的观察值

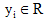是输出序列集y的观察值

M 次项式是解决问题的模型

W为参数

解决如上问题按照经验风险最小化策略求解参数即可，即数学表达：

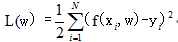
损失函数为平方损失，1/2是便于计算。然后将模型公式和训练数据代入风险最小化公式：

，最后采用最小二乘法（过程略）求解。

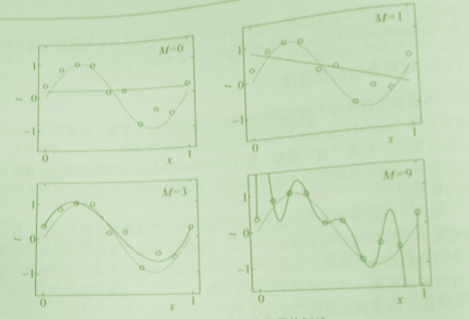
3.3 实例分析

如上图给出M=0,1,3,9的多项式函数的拟合情况，当M=0时，多项式为一个常数，数据拟合很差，当M=1时，多项式曲线为一条直线，拟合依旧差；当M=9时，多项式通过每一个点，训练误差0，从训练数据拟合角度分析，效果最好，但是训练数据本身很多噪音，对未来数据预测能力差，达不到预期的效果。这就是过拟合，虽然训练数据好但是未知数据差。当M=3时，多项式曲线对训练数据拟合效果比较好，对未知数据拟合也很好，其模型也简单，可以选择。总结：模型选择时，不仅仅考虑对已知数据的预测能力，还有考虑对未知数据的预测能力。

训练误差和测试误差与模型复杂度的关系如下图：

可知，当模型复杂度增大时候，训练误差会逐渐减少趋近于0，而测试误差会先减小到最小值后又增大。当选择模型复杂度过大时，过拟合问题就会出现。

3.4 补充

NLP序列句子识别标注实例更好理解本节。（以下实例便于理解假设的，不是特别严谨）

训练数据集T={(南 B),(海 I),(是 I), (中 I),(国 I),(领 I), (土 I),(。 O) }未知数据P={(不 B), (容 I),(争I),( 议 I),（。 O）}采用BIO标注，B代表句子开始，I代表中间连续词，O代表句子。结束。假设采用模型M识别, M次多项式的模型

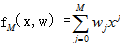
完成下面句子识别。

结果分析：

M=0时候，模型一个常数效果很差，识别如下：

M=1时候，模型一条直线效果很差，识别如下：

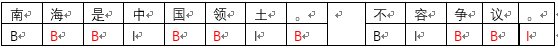
M=3时候，模型曲线拟合基本合理，且未知数据预测较好，识别如下：

M=9时候，模型一条直线效果很差，识别如下：

训练数据集：

实验可知：左侧为训练模型的数据，右侧为测试模型的数据。当M=0时，训练误差和测试误差都很大；当M=1时，训练误差和测试误差较大；当M=3时，训练误差比M=9的训练误差大，总体训练误差还好，但是，预测误差却小于M=9时的预测误差。综合比较，选择M=3的模型效果会更好。综上，旨在让大家更好理解概念理论知识。

4 参考文献

---

【1】 数据挖掘概念与技术（364--386） 韩家炜

【2】 数据挖掘：R语言实战（274--292） 黄文、王正林

【3】 统计自然语言处理基础 （166—169） 宛春法等译

【4】 统计学习方法（10---13） 李航

5 自然语言相关系列文章

---

【自然语言处理：马尔可夫模型（一）】：初识马尔可夫和马尔可夫链

【自然语言处理：马尔可夫模型（二）】：马尔可夫模型与隐马尔可夫模型

【自然语言处理：马尔可夫模型（三）】：向前算法解决隐马尔可夫模型似然度问题

【自然语言处理：马尔可夫模型（四）】：维特比算法解决隐马尔可夫模型解码问题（中文句法标注）

【自然语言处理：马尔可夫模型（五）】：向前向后算法解决隐马尔可夫模型机器学习问题

声明：关于此文各个篇章，本人采取梳理扼要，顺畅通明的写作手法。系统阅读相关书目和资料总结梳理而成，旨在技术分享，知识沉淀。在此感谢原著无私的将其汇聚成书，才得以引荐学习之用。其次，本人水平有限，权作知识理解积累之用，难免主观理解不当，造成读者不便，基于此类情况，望读者留言反馈，便于及时更正。本文原创，转载请注明出处：谈谈学习器模型的评估指标。