codeforces 85D D. Sum of Medians 线段树

D. Sum of Medians

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In one well-known algorithm of finding the k-th order statistics we should divide all elements into groups of five consecutive elements and find the median of each five. A median is called the middle element of a sorted array (it's the third largest element for a group of five). To increase the algorithm's performance speed on a modern video card, you should be able to find a sum of medians in each five of the array.

A sum of medians of a sorted k-element set S = {a₁, a₂, ..., a_k}, where a₁ < a₂ < a₃ < ... < a_k, will be understood by as

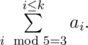
The 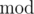operator stands for taking the remainder, that is 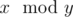stands for the remainder of dividing x by y.

To organize exercise testing quickly calculating the sum of medians for a changing set was needed.

Input

The first line contains number n (1 ≤ n ≤ 10⁵), the number of operations performed.

Then each of n lines contains the description of one of the three operations:

• add x — add the element x to the set;
• del x — delete the element x from the set;
• sum — find the sum of medians of the set.

For any add x operation it is true that the element x is not included in the set directly before the operation.

For any del x operation it is true that the element x is included in the set directly before the operation.

All the numbers in the input are positive integers, not exceeding 10⁹.

Output

For each operation sum print on the single line the sum of medians of the current set. If the set is empty, print 0.

Please, do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams (also you may use the %I64d specificator).

Examples

Input

6
add 4
add 5
add 1
add 2
add 3
sum

Output

3

Input

14
add 1
add 7
add 2
add 5
sum
add 6
add 8
add 9
add 3
add 4
add 10
sum
del 1
sum

Output

5
11
13

#include<bits/stdc++.h>
using namespace std;
#define ll unsigned long long
#define pi (4*atan(1.0))
#define eps 1e-14
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=2e5+,M=1e6+,inf=1e9+;
const ll INF=1e18+,mod=;
int n,tree[N];
int lowbit(int x)
{
    return x&-x;
}
void update(int x,int c)
{
    while(x<1e5+)
    {
        tree[x]+=c;
        x+=lowbit(x);
    }
}
int getsum(int x)
{
    int sum=;
    while(x>)
    {
        sum+=tree[x];
        x-=lowbit(x);
    }
    return sum;
}
struct is
{
    int lazy;
    ll ans[];
}a[N<<];
ll temp[];
void pushup(int pos)
{
    for(int i=;i<;i++)
        a[pos].ans[i]=a[pos<<].ans[i]+a[pos<<|].ans[i];
}
void change(int pos,int x)
{
    x=(x%+)%;
    int ji=;
    for(int i=;i<;i++)
        temp[i]=a[pos].ans[i];
    for(int i=x;i<;i++)
        a[pos].ans[i]=temp[ji++];
    for(int i=;i<x;i++)
        a[pos].ans[i]=temp[ji++];
}
void pushdown(int pos)
{
    if(a[pos].lazy)
    {
        a[pos<<].lazy+=a[pos].lazy;
        a[pos<<|].lazy+=a[pos].lazy;
        change(pos<<,a[pos].lazy);
        change(pos<<|,a[pos].lazy);
        a[pos].lazy=;
    }
}
void build(int l,int r,int pos)
{
    a[pos].lazy=;
    memset(a[pos].ans,,sizeof(a[pos].ans));
    if(l==r)return;
    int mid=(l+r)>>;
    build(l,mid,pos<<);
    build(mid+,r,pos<<|);
}
void update(int L,int R,int c,int l,int r,int pos)
{
    if(L<=l&&r<=R)
    {
        a[pos].lazy+=c;
        change(pos,c);
        return;
    }
    pushdown(pos);
    int mid=(l+r)>>;
    if(L<=mid)
        update(L,R,c,l,mid,pos<<);
    if(R>mid)
        update(L,R,c,mid+,r,pos<<|);
    pushup(pos);
}
void point(int p,int k,int c,int l,int r,int pos)
{
    if(l==r)
    {
        a[pos].ans[k]+=c;
        return;
    }
    pushdown(pos);
    int mid=(l+r)>>;
    if(p<=mid)
        point(p,k,c,l,mid,pos<<);
    else
        point(p,k,c,mid+,r,pos<<|);
    pushup(pos);
}
char str[N][];
int b[N];
int s[N],cnt;
int getpos(int x)
{
    int pos=lower_bound(s+,s++cnt,x)-s;
    return pos;
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%s",str[i]);
        if(str[i][]=='a'||str[i][]=='d')
        {
            scanf("%d",&b[i]);
            s[++cnt]=b[i];
        }
    }
    sort(s+,s++cnt);
    cnt=max(,cnt);
    build(,cnt,);
    for(int i=;i<=n;i++)
    {
        //cout<<str[i]<<endl;
        if(str[i][]=='a')
        {
            int x=getpos(b[i]);
            int now=getsum(x-);
            now%=;
            //cout<<x<<" "<<now<<" "<<b[i]<<endl;
            update(x,);
            update(x+,cnt,,,cnt,);
            point(x,now,b[i],,cnt,);
        }
        else if(str[i][]=='d')
        {
            int x=getpos(b[i]);
            int now=getsum(x-);
            now%=;
            update(x,-);
            point(x,now,-b[i],,cnt,);
            update(x+,cnt,-,,cnt,);
        }
        else
            printf("%lld\n",a[].ans[]);
        //printf("%lld\n",a[1].ans[2]);
    }
    return ;
}