NOIp 2011 mayan游戏搜索

题目描述

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个 7 行5 列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1 、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图6 到图7 ）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图1 和图2）；

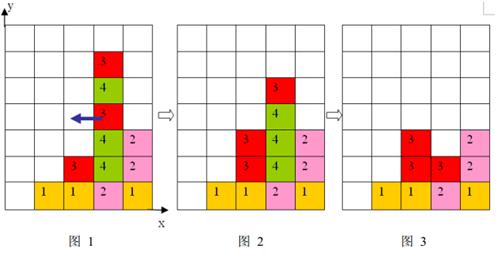
2 、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：

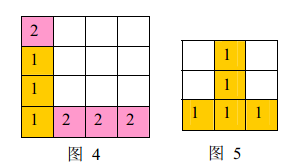
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图4 ，三个颜色为1 的方块和三个颜色为 2 的方块会同时被消除，最后剩下一个颜色为 2 的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形，5 个方块会同时被消除）。

3 、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0 ），将位于（3, 3 ）的方块向左移动之后，游戏界面从图 1 变成图 2 所示的状态，此时在一竖列上有连续三块颜色为4 的方块，满足消除条件，消除连续3 块颜色为4 的方块后，上方的颜色为3 的方块掉落，形成图 3 所示的局面。

输入输出格式

输入格式：

输入文件mayan.in，共 6 行。

第一行为一个正整数n ，表示要求游戏通关的步数。

接下来的5 行，描述 7*5 的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个0 结束，自下向上表示每竖列方块的颜色编号（颜色不多于10种，从1 开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式：

输出文件名为mayan.out。

如果有解决方案，输出 n 行，每行包含 3 个整数x，y，g ，表示一次移动，每两个整数之间用一个空格隔开，其中（x ，y）表示要移动的方块的坐标，g 表示移动的方向，1 表示向右移动，-1表示向左移动。注意：多组解时，按照 x 为第一关健字，y 为第二关健字，1优先于-1 ，给出一组字典序最小的解。游戏界面左下角的坐标为（0 ，0 ）。

如果没有解决方案，输出一行，包含一个整数-1。

输入输出样例

输入样例#1：

输出样例#1：

2 1 1
3 1 1
3 0 1

说明

【输入输出样例说明】

按箭头方向的顺序分别为图6 到图11

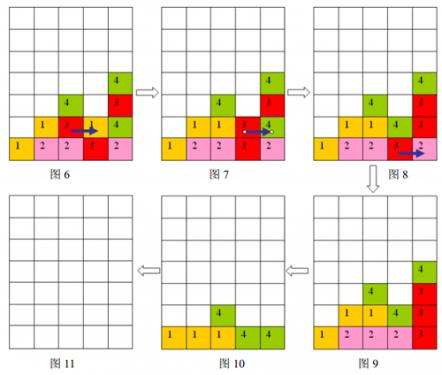
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是：（2 ，1 ）处的方格向右移动，（3，1 ）处的方格向右移动，（3 ，0）处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】

对于30% 的数据，初始棋盘上的方块都在棋盘的最下面一行；

对于100%的数据，0 < n≤5 。

点击此处提交

搜索。

因为要求字典序最小所以都右移除非那个方格为空。

代码如下：

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #define For(i,x,y) for(int i=x;i<=y;++i)
 using namespace std;
 int a[][];
 int cnt[];int n;    int ncnt[];
 int qx[],qy[],qg[];
 inline bool check()
 {
     int v[][];memset(v,,sizeof(v));
     memset(ncnt,,sizeof(ncnt));
     For(i,,)
     {
         For(j,,)
         {
             if(a[i][j])a[i][ncnt[i]++]=a[i][j];
         }
         For(j,ncnt[i],)a[i][j]=;
     }
     bool flag=false;
     For(i,,)
     {
         For(j,,)
         {
             if(!a[i][j])continue;
             int k=;int u=a[i][j];
             for(k=j+;a[i][k]==u;++k);
             if(k-j>=){flag=;For(p,j,k-)v[i][p]=;}
             for(k=i+;a[k][j]==u;++k);
             if(k-i>=){flag=;For(p,i,k-)v[p][j]=;}
         }
     }
     if(flag)For(i,,)For(j,,)if(v[i][j]==)a[i][j]=;
     For(i,,)cnt[i]=ncnt[i];
     return flag;
 }
 inline bool done()
 {
     For(i,,)For(j,,)if(a[i][j])return ;return ;
 }
 void dfs(int step)
 {
     int tmp[][],tcnt[];
     while(check());
     if(done())
     {
         For(i,,step-)
             printf("%d %d %d\n",qx[i],qy[i],qg[i]);
         exit();
     }
     if(step==n+)return;
     For(i,,)For(j,,)tmp[i][j]=a[i][j];
     For(i,,)tcnt[i]=cnt[i];
     For(i,,)
     {
         For(j,,cnt[i])
         {
             if(i!=&&a[i][j]!=a[i+][j]&&a[i][j])
             {
                 swap(a[i][j],a[i+][j]);qx[step]=i;qy[step]=j;qg[step]=;
                 dfs(step+);
                 For(i,,)For(j,,)a[i][j]=tmp[i][j];
                 For(i,,)cnt[i]=tcnt[i];
             }
             if(i!=&&!a[i-][j])
             {
                 swap(a[i-][j],a[i][j]);
                 qx[step]=i;qy[step]=j;qg[step]=-;
                 dfs(step+);
                 swap(a[i-][j],a[i][j]);
                 For(i,,)For(j,,)a[i][j]=tmp[i][j];
                 For(i,,)cnt[i]=tcnt[i];
             }
         }
     }
 }
 int main()
 {
     cin>>n;
     For(i,,)
     {
         int x;cin>>x;
         while(x)
         {
             a[i][cnt[i]++]=x;
             cin>>x;
         }
     }
     dfs();
     cout<<-;
 }