Day 4 上午

内容提要

进制转换

高精度

数论：筛法，gcd/exgcd，逆元

---

进制转换

10=2^3+2^0=1010（2）
10=3^2+3^0=101（3）

10进制x-->k进制：短除法

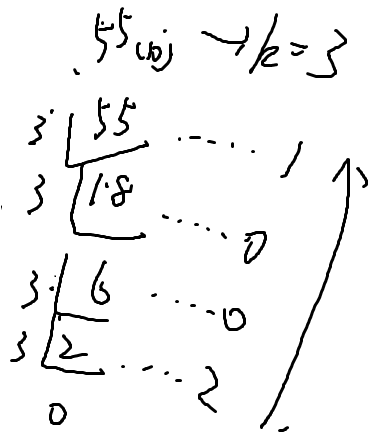
k进制x-->10进制：根据定义转换
XnXn-1Xn-2....X0(k)
=Xn*k^n+Xn-1*k^(n-1)+....+X0*k^0

计算机中常用的进制：2,8,10,16

c++中给变量赋一个二进制值：加一个前导0
int a=01001---a=9

十六进制int a=0x1001=16^3+16^0=4097
十六进制中：a--10,b--11,c--12,d--13,e--14,f--15
0x3f3f3f3f=3*16^7+15*16^6+3*16^5+...

高精度：竖式加减乘除法
存储：用一个数组存他的每一位（反着存）
因为如果正着存的话数位就不能对齐了

先写一个int的版本，然后把int全部替换为高精
我们希望写一个好的高精模板，使得这个东西可以直接用
面向对象的编程方法（其实就是模块化，用很多函数）

我们先设一个结构体

struct gaojing
{
    int z[];//用来存这个数的数组
    int l;//这个高精度是个l位的数
};

这里很坑的点就是对不同的编译器版本，结构体里的数会不一样
比如dev本地的版本会全都赋值0,
但是这显然是不对的，因为0是个n位的数
怎么初始化？
结构体的构造函数，就是每一次声明一个变量的时候调用一次

struct gaojing
{
    int z[];//用来存这个数的数组
    int l;//这个高精度是个l位的数
    gaojing()
    {
        l=;
        memset(z,,sizeof(z));//构造函数
     }
};

已经非常接近线性筛了
要实现什么运算？+-*/%
<,<=,>,>=,==,!=
cin>>,cout<<
重载运算符
两个高精计算，返回高精值

gaojing operator + (gaojing a,gaojing b)
{
    bulabula
    return ans;
}

但是这样写会有问题

(惊不惊喜，意不意外，刺不刺激

c++再调用函数时，如果没有取地址符&
做了一个备份再调用
比如你设了一个x
调用f(x)时先给x做一个备份x'，然后把x'传给x
如果加上&，就是直接把x传给它
这里如果拷贝一个超大的高精度的数组，就有可能会tle
所以我们加上取地址符&

gaojing operator + (gaojing &a,gaojing &b)
{
    bulabulabula
    return ans;
}

但其实这样还有问题

(惊不惊喜，意不意外，刺不刺激

因为比如你手抖把a改了，那么a原本的值就会变
所以我们再加上一个const
而且如果你想要调用stl，就必须要加上const

 gaojing operator + (const gaojing &a,const gaojing &b)
{
    bulabulabula

    return c;
}

这样就好了

完整的重载

gaojing operator + (const gaojing &a,const gaojing &b)
{
    gaojing c;
    int l=max(a.l,b.l);
    for(int i=;i<l;i++)
    {
        c.z[i]+=a.z[i]+b.z[i];
        c.z[i+]+=c.z[i]/;
        c.z[i]=c.z[i]%;
    }//模拟竖式的运算过程
    if(c.z[l]!=)l++;//看看是否还有进位
    c.l=l;

    return c;
}

接下来是cin和cout的重载

cin：

friend istream& operator>>(istream&cin,gaojing &a)

    {
        static char s[];//static静态变量
        cin>>s;
        int l=strlen(s);//算长度
        for(int i=;i<l;i++)
            a.z[i]=s[l-i-]-'';
        //把读进来的字符串存储
        a.l=l;
        return cin;//要求返回cin
    }

其中static类似于全局变量

不能在函数里边开数组的局部变量

如果要开的话就要加static

friend:友元函数 istream:读入流 ，用cin这个读入函数把它读入到a中

用字符串读入

第一行和最后一行当做模板记就可以

cout:

friend ostream& operator<<(ostream&cin,const gaojing &a)
{
    for(int i=a.l-;i>=;i--)
        cout<<a.z[i];

    return cout;
}

注：这个东西要放到结构体内，因为有友元函数（虽然我不知道为什么，但是记住就好了）

完整的就是这样：

struct gaojing
{
    int z[];
    int l;
    gaojing()
    {
        l=;
        memset(z,,sizeof(z));
    }
    friend istream& operator>>(istream&cin,gaojing &a)

    {
        static char s[];
        cin>>s;
        int l=strlen(s);
        for(int i=;i<l;i++)
            a.z[i]=s[l-i-]-'';
        a.l=l;

        return cin;
    }

    friend ostream& operator<<(ostream&cin,const gaojing &a)
    {
        for(int i=a.l-;i>=;i--)
            cout<<a.z[i];

        return cout;
    }
};

下面是高精度乘法

同样是模拟竖式计算

gaojing operator * (const gaojing &a,const gaojing &b)
{
    gaojing c;
    for(int i=;i<a.l;i++)
        for(int j=;j<b.l;j++)
            c.z[i+j]+=a.z[i]*b.z[j];
            //第i位和第j位相乘贡献第i+j位 

    c.l=a.l+b.l;//位数最多是这些
    for(int i=;i<c.l;i++)
    {
        c.z[i+]+=c.z[i]/;
        c.z[i]=c.z[i]%;
    }//处理进位
    while(c.l>&&c.z[c.l]==)
        c.l--;
    c.l++;//找到第一个不等于0的位置，就是他的最高位
    //因为从0开始，所以位数+1

    return c;
}

数论：
π(x)≈x/log x

质数
只有1和自身作为因子的数叫做质数
以π(x)表示不超过 x 的素数的个数，可以证
lim π(x) ln x ÷ x = 1

最常见的判断素数的方法：

bool is_prime(int x)
{
    if(x<=)return false;
    for(int a=;a<x;a++)
        if(x%a==) return false;
    return true;
}

复杂度O（x）

可以做一些优化

x=a*b>=a*a,a<=b,x>=a^2,a<=√x

bool is_prime(int x)
{
    if(x<=)return false;
    for(int a=;a*a<x;a++)
        if(x%a==) return false;
    return true;
}

复杂度降到O（√n）

但是如果我们想要求一个区间之内的所有质数呢？
一个一个代进去显然会tle
复杂度O(n√n)

所以我们需要一种更快的方法
筛法

两种非线性的算法:

1.
我们枚举所有数，并把它的所有倍数标记成合数
复杂度O(n logn)
n/2+n/3+n/4+....+n/n
≈n(1+1/2+1/3+...+1/n)
≈n log n

for(a=;a<=n;a++)
    for(int b=+;b<=n;b+=a)
        not_prime[b]=true; 

2.
实际上，我们只需要筛掉质数的倍数，因为一个合数的倍数一定是它的质因子的倍数

for(a=;a<=n;a++)
    if(not_prime[a]=false)
        for(int b=+;b<=n;b+=a)
            not_prime[b]=true; 

复杂度O(n loglog n)

已经非常接近线性筛了

线性筛就是保证每个数只被他最小的质因子筛掉
这样复杂度就降到O(n)了

代码：

memset(not_prime,,sizeof(not_prime));//初始化为都是质数
not_prime[]=true;//1不是质数
for(int i=;i<=n;i++)
{
    if(!not_prime[i])    prime[++prime_count]=i;
    //如果i还没有被标记为不是质数 ，就把i加到质数表里面
    for(int j=;j<=prime_count;j++)
    {
        if(prime[j]*i>n) break;//枚举i的质数倍
        not_prime[prime[j]*i]=true;
        if(i%prime[j]==) break;
        //如果i是第j个质数的倍数，就跳出循环
        //因为i有prime[j]这个因子，再枚举prime[j]就会变大
        //break掉就可以保证一定是被它的最小质因子筛掉
     }
}

用来处理积性函数

最大公因子
gcd(a,b)=max (x|a,x|b)

gcd(121,1001)=11

辗转相除法
gcd(a,b)=gcd(b,a%b)

int gcd(int a,int b)
{
    if(b==) return a;//gcd(a,0)=a
    else return gcd(b,a%b);
}

c++自带的求最大公因数的__gcd（双下划綫），但是最好不要用

gcd(a,b)=g
==>ax+by=g(x,y∈Z)

如：
gcd(30,12)=6
==>1*30-2*12=6
==>-1*30+3*12=6
显然结果有无数组

已经知道gcd(a,b)=g
求一组ax+by=g解

拓展欧几里得算法：

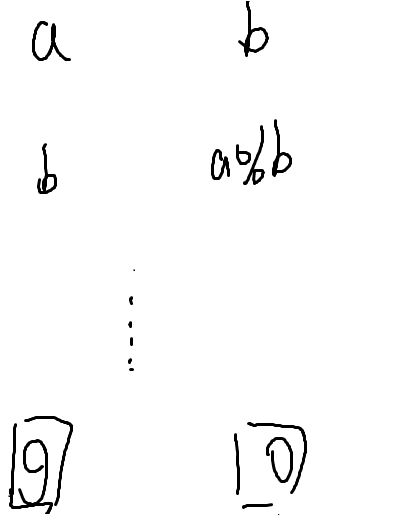
不管进行到那一层，最大公约数都是g
也就是在每一层都可以找到这样的x，y

显然最后一层是最好找的
一定有1*g+0*0=g
然后考虑一层一层的推上去
我们把a%b换一种写法，写成带余除法的形式
余数=被除数-除数*商
xb+y(a-a/b*b)=g(/是下取整)
拆开括号合并同类项
ya+(x-y*(a/b))b=g
而上一层是x'a+y'b=g
所以x'=y,y'=x-y*(a/b)

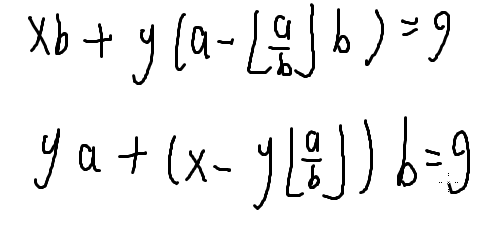
int exgcd(int a,int b,int &x,int &y)
{
    if(b==)//到了最底层
    {
        x=,y=;//这是一组解
        return a;//最大公因数
    }
    else
    {
        int g=exgcd(b,a%b,x,y);
        int t=x;
        x=y,y=t-a/b*x;//x'=y,y'=x-y*(a/b)
        return g;
    }
}

逆元
希望能边乘边除边取模得到模运算的正确结果

费马小定理：
对于质数p，任取一个1~p-1的数
x^(p-1)%p=1
两边同时除以x
x^(p-2)%p=(1/x)%p
也就是在取模意义下,a/b=a*(1/b)=a*b^(p-2)(mod p)（改符号）
b^(p-2)就是b的逆元

当p不是质数时，需要用到欧拉定理

x^(φ(m))=1(mod m)改符号
φ(m)表示1~m中有多少个数和m互质
求φ的公式
将m分解质因数
m=p1^k1*p2^k2......*pn^kn
φ(m)=m*(1-1/p1)(1-1/p2)....(1-1/pn)

当p为质数时，φ(p)=p-1
所以费马小定理就是欧拉定理的拓展
当m不是质数时，除以x等于乘x^(φ(m)-1)