洛谷 P2096 最佳旅游线路

某旅游区的街道成网格状。其中东西向的街道都是旅游街，南北向的街道都是林阴道。由于游客众多，旅游街被规定为单行道，游客在旅游街上只能从西向东走，在林阴道上则既可从南向北走，也可以从北向南走。

阿龙想到这个旅游街游玩，他的好友阿福给了他一些建议，用分值表示所有旅游街相邻两个路口之见的街道值得游览的程度，分值是从-100到100的整数，所有林阴道不打分。所有分值不可能全是负分。如图：

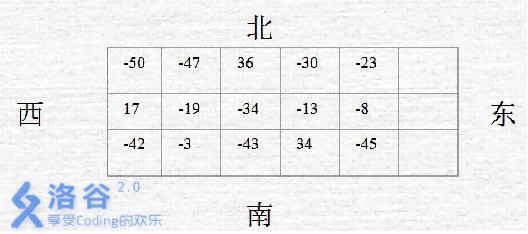
输入输出格式

输入格式：

输入文件的第一行是两个整数m和n,之间用一个空格隔开，m表示有m条旅游街（1≤m≤100 ），n 表示有(n+1)条林阴道（1≤n≤20001 ）。接下来的m行依次给出了由北向南每条旅游街的分值信息。每行有n个整数，依次表示了自西向东旅游街每一小段的分值。同一行相邻两个数之间用一个空格隔开。

输出格式：

输出文件只有一行，是一个整数，表示你的程序找到的最佳游览线路的总分值。

输入输出样例

输入样例#1：

3 5
-50 -47 36 -30 -23
17 -19 -34 -13 -8
-42 -3 -43 34 -45

输出样例#1：

84

e，边做题，边写题解，大致读了遍题，是道 贪心，
那么我们分析一下题，图大概是下面这个样子：

------------

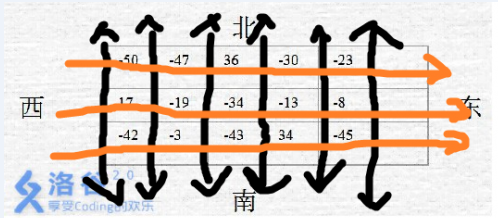
竖直方向可以随便走嘛，所以求出每一列
的最大值，再做比较就可以了。

------------
but，命运多舛，交了一遍，80分，有两个点过不了，重读遍题发现：对了，不一定要在最右边结束，也不一定在最左边开始，这点很重要，这才AC了此题。
先上代码

------------

八十分版

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 #define ll long long
 #define R register
 #define mmax 20002
 ll n,m,maxx=-0x7fffffff,ans;
 ll tu[][mmax],da[mmax];
 int main()
 {
     /*freopen(".in","r",stdin);
     freopen(".out","w",stdout);*/
     cin>>m>>n;
     for(int i=;i<=m;i++)
     for(int j=;j<=n;j++)
     {
     cin>>tu[i][j]; //输入
     }
     /*for(int i=1;i<=m;i++)
         for(int j=1;j<=n;j++)
     {
     cout<<tu[i][j]<<" ";
     }*/

     for(int i=;i<=n;i++)
     {
         maxx=-0x7ffffff;
         for(int j=;j<=m;j++)
             {
                if(tu[j][i]>maxx)//注意i和j的顺序
                {
                da[i]=tu[j][i];
                maxx=tu[j][i];//
                }

             }
         }
         /*for(int i=1;i<=n;i++)
         {
             cout<<da[i]<<" ";//最大值
         }*/
         ll qzh1=,qzh2=;
         for(int i=;i<=n;i++)
         {
             qzh1=qzh2+da[i];
             qzh2=qzh1;
             if(ans<qzh1) ans=qzh1;
         }
         cout<<ans<<endl;
     /*fclose(stdin);
     fclose(stdout);*/
     return ;
 }

------------
一百分版

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 #define ll long long
 #define II int
 #define R register
 #define mmax 20002
 #define inf 0x7ffffff
 II n,m,ans;
 II tu[][mmax],da[mmax];
 II mxsum(II *x){   //最大子串和
     II th=;
     II mx=;
     for(R II i=;i<=n;++i){
         th+=x[i];
         if(th<)th=;
         else if(th>mx)mx=th;
     }
     return mx;
 }
 int main()
 {
     /*freopen(".in","r",stdin);
     freopen(".out","w",stdout);*/
     cin>>m>>n;
     for(int i=;i<=m;i++)
     for(int j=;j<=n;j++)
     {
         cin>>tu[i][j]; //输入
     }
     for(int i=;i<=n;i++)
     {
         da[i]=-inf;
         for(int j=;j<=m;j++)
            if(tu[j][i]>da[i])//注意i和j的顺序
            {
                    da[i]=tu[j][i];、、每列最大值
            }
     }
     cout<<mxsum(da)<<endl;
     /*fclose(stdin);
     fclose(stdout);*/
     return ;
 }

就这样了，好好打，别变棕哟QWQ。