URAL —— 1255 & HDU 5100——Chessboard ——————【数学规律】

用 k × 1 的矩形覆盖 n × n 的正方形棋盘

用 k × 1 的小矩形覆盖一个 n × n 的正方形棋盘，往往不能实现完全覆盖（比如，有时候 n × n 甚至根本就不是 k 的整倍数）。

解题思路：

转自：http://www.matrix67.com/blog/archives/5900

用 k × 1 的矩形覆盖 n × n 的正方形棋盘

用 k × 1 的小矩形覆盖一个 n × n 的正方形棋盘，往往不能实现完全覆盖（比如，有时候 n × n 甚至根本就不是 k 的整倍数）。不过，在众多覆盖方案中，总有一种覆盖方案会让没有覆盖到的方格个数达到最少，我们就用 m(n, k) 来表示这个数目。求证：不管 n 和 k 是多少， m(n, k) 一定是一个完全平方数。

如果 n < k ，那么很明显，棋盘里一个小矩形也放不下，因而 m(n, k) = n2 ，这是一个完全平方数。下面我们就只考虑 n ≥ k 了。

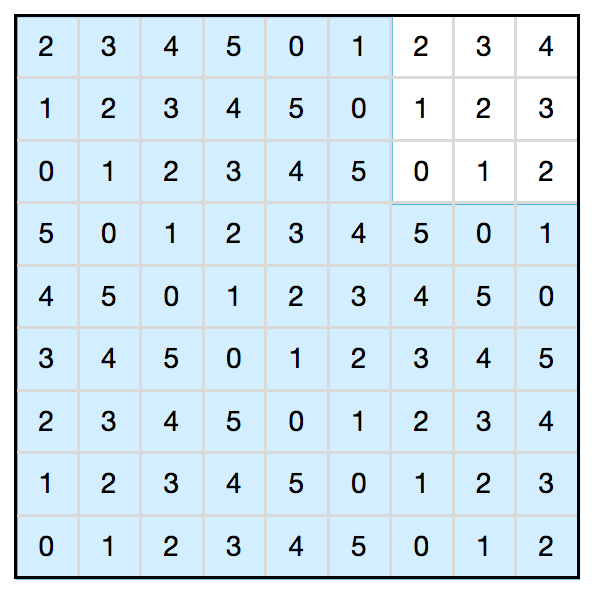
我们先来证明这样一个事实：如果某个覆盖方案当中，仅剩下一个 s × s 的小正方形区域没有覆盖到，其中 s ≤ k / 2 ，那么这样的方案一定是最优的。首先，在棋盘中的每个格子里都填上一个数，使得从最左下角出发，各个对角线上的数依次为 0, 1, 2, …, k – 1, 0, 1, 2, …, k – 1, … （上图所示的是 k = 6 的情况）。那么，把一个 k × 1 的小矩形放在棋盘中的任意位置，它总会覆盖每种数字各一个。假设某个覆盖方案当中，仅剩下一个 s × s 的小正方形区域没有覆盖到。注意到，任意一个 s × s 的小正方形区域里最多只会出现 2s – 1 种不同的数，因此如果 s ≤ k / 2 ，那么这个 s × s 的小正方形区域里一定会缺失至少一种数，比方说 x （在上图中，右上角的那个 3 × 3 的空白区域里就缺数字 5 ，因而我们可以取 x = 5 ）。由此可以推出，此时小矩形的数目已经达到了最大值，任何其他覆盖方案都不可能包含更多的小矩形，因为每个小矩形都必然会覆盖到一个 x ，然而在刚才的覆盖方案中，所有的 x 都已经被覆盖到了。

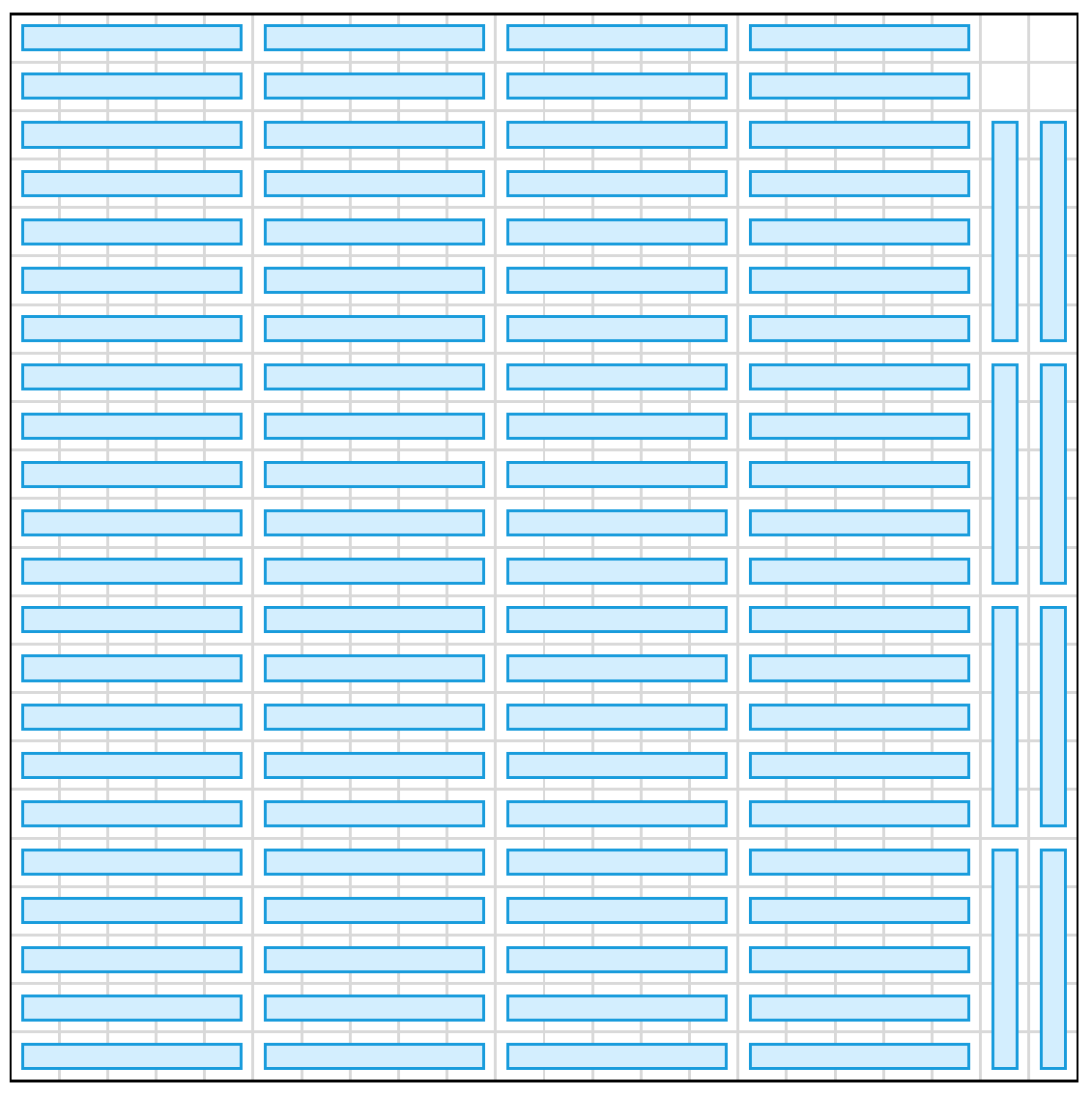
有趣的是，当 n ≥ k 时，让整个棋盘仅剩一个边长不超过 k / 2 的小正方形区域没有覆盖到，这是一定能做到的。不妨把 n 除以 k 的余数记作 r 。如果 r ≤ k / 2 ，那么我们可以直接用横着的小矩形从左向右填充棋盘，再用竖着的小矩形填充余下的部分，最终会剩下 r × r 的小正方形区域。上图所示的就是 n = 22 并且 k = 5 的情况，注意到 22 除以 5 的余数为 2 ，确实小于等于除数 5 的一半。可见，对于这类情况，我们都有 m(n, k) = r2 ，这是一个完全平方数。

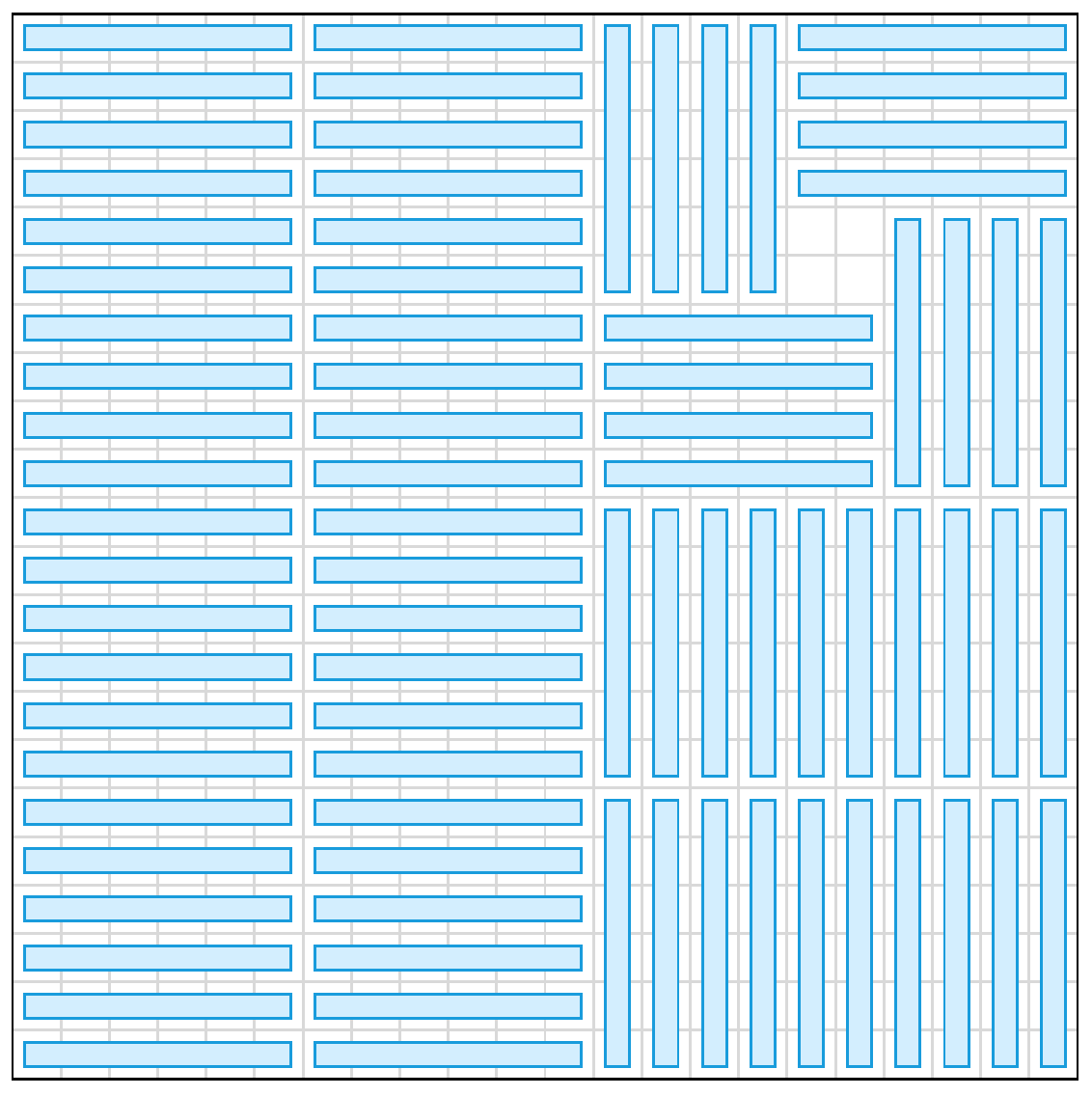
如果 r > k / 2 呢？我们可以用和刚才类似的方法填充棋盘，使得棋盘右上角仅剩一个 (r + k) × (r + k) 的正方形区域。然后再用 4r 个小矩形像风车一样填充这个 (r + k) × (r + k) 的区域，使得正中间只剩下一个边长为 k – r 的小正方形区域。由于 k – r < k / 2 ，因而此时的覆盖方案再次达到最优。上图所示的就是 n = 22 并且 k = 6 的情况，注意到 22 除以 6 的余数为 4 ，确实大于除数 6 的一半。可见，对于这类情况，我们有 m(n, k) = (k – r)2 ，这仍然是一个完全平方数。

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<bitset>
/*
solution: http://www.matrix67.com/blog/archives/5900
*/
#include<iostream>
using namespace std;
int main(){
    int n,k;
    while(scanf("%d%d",&n,&k)!=EOF){
        if(n < k){
            puts("0");
            continue;
        }
        int r = n%k;
        if(r <= k/2){
            printf("%d\n",(n*n - r*r)/k );
        }else{
            printf("%d\n",(n*n - (k-r)*(k-r))/k );
        }
    }
    return 0;
}