[学习笔记]动态dp
其实就过了模板。
感觉就是带修改的dp
【模板】动态dp
给定一棵n个点的树，点带点权。
有m次操作，每次操作给定x,y表示修改点x的权值为y。
你需要在每次操作之后求出这棵树的最大权独立集的权值大小。
n,m<=1e5
参考题解：shadowice1984
n^2 DP简单又自然。
但是对于1e5次修改就不行了。
每一次修改会影响整个到根的链上的值。
采用树剖。
ldp[i][0/1]表示i选不选，对于所有的轻儿子dp值。
dp[i][0/1]表示i选不选，对于总共的所有儿子的dp值。
ldp[i][0]=∑max(ldp[lightson][1],ldp[lightson][0])
ldp[i][1]=∑ldp[lightson][0]
dp[i][0]=ldp[i][0]+max(dp[heavyson][1],dp[heavyson][0])
dp[i][1]=ldp[i][1]+dp[heavyson][0]
可以先把这个dp都求出来。
然后怎么维护？自然要用线段树维护dfs序。
采用矩阵。
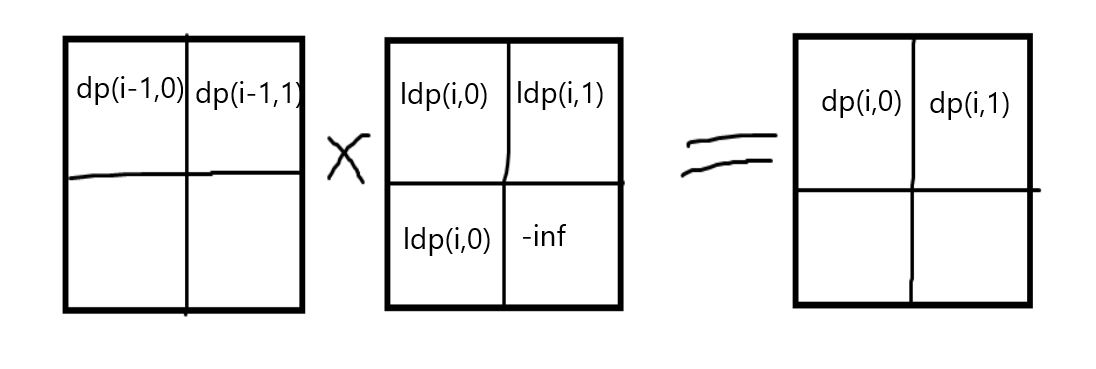
a*b定义为：
c[i][j]=max(a[i][k]+b[k][j])
有结合律。
线段树维护区间矩阵乘积。（注意从右往左乘，自下而上）
只要在最前面乘上一个初始矩阵
第一行是0，第二行是-inf的矩阵。
就可以求出某个点的最终dp值了。
修改的时候，暴力修改这个 点的ldp0，ldp1
但是还会影响这个fa[top[x]]的ldp0,ldp1
所以要求出dp[top[x]],dp[top[y]]为了避免常数过大，
用一个数组记录dp值，然后把前后两次最大值的差值来修改fa[top[x]]的ldp0,ldp1
然后跳一条链，到fa[top[x]]
这样单次修改log^2n
每次返回max(dp[1][0],dp[1][1])
普通线段树版：（3000ms）
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define mid ((l+r)>>1)
using namespace std;
typedef long long ll;
il void rd(int &x){
char ch;x=;bool fl=false;
while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
for(x=numb;isdigit(ch=getchar());x=x*+numb);
(fl==true)&&(x=-x);
}
namespace Miracle{
const int N=1e5+;
const int inf=0x3f3f3f3f;
int n,m;
struct node{
int nxt,to;
}e[*N];
int hd[N],cnt;
void add(int x,int y){
e[++cnt].nxt=hd[x];
e[cnt].to=y;
hd[x]=cnt;
}
struct tr{
int a[][];
void init(int x,int y){//x:ldp0 y:ldp1
a[][]=x,a[][]=x;
a[][]=y,a[][]=-inf;
}
void pre(){
memset(a,-inf,sizeof a);
}
void st(){
a[][]=,a[][]=-inf,a[][]=-inf,a[][]=;
}
tr operator *(const tr& b){
tr c;c.pre();
for(reg i=;i<=;++i){
for(reg k=;k<=;++k){
for(reg j=;j<=;++j){
c.a[i][j]=max(c.a[i][j],a[i][k]+b.a[k][j]);
}
}
}return c;
}
void op(){
cout<<left<<setw()<<a[][]<<" "<<left<<setw()<<a[][]<<endl;
cout<<left<<setw()<<a[][]<<" "<<left<<setw()<<a[][]<<endl;
cout<<endl;
}
}s[N],t[*N],A;
int dfn[N],top[N],dfn2[N],fdfn[N],sz[N],dep[N],son[N];
int nd[N];//tot;//num of heavy chain
int fa[N];
int df;
int ldp[N][],dp[N][];
int w[N];
void dfs1(int x,int d){
dep[x]=d;
sz[x]=;
for(reg i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa[x]) continue;
fa[y]=x;
dfs1(y,d+);
if(sz[y]>sz[son[x]]){
son[x]=y;
}
}
}
void dfs2(int x){
dfn[x]=++df;fdfn[df]=x;
if(!top[x]) {
top[x]=x;nd[top[x]]=x;
}
if(son[x]) top[son[x]]=top[x],nd[top[x]]=son[x],dfs2(son[x]); dp[x][]=w[x];
ldp[x][]=w[x];
for(reg i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==son[x]||y==fa[x]) continue;
dfs2(y);
ldp[x][]+=max(dp[y][],dp[y][]);
ldp[x][]+=dp[y][];
}
if(son[x]){
dp[x][]=ldp[x][]+dp[son[x]][];
dp[x][]=ldp[x][]+max(dp[son[x]][],dp[son[x]][]);
}
s[x].init(ldp[x][],ldp[x][]);
}
void pushup(int x){
t[x]=t[x<<|]*t[x<<];
}
void build(int x,int l,int r){
if(l==r){
t[x]=s[fdfn[l]];return;
}
build(x<<,l,mid);build(x<<|,mid+,r);
pushup(x);
}
tr query(int x,int l,int r,int L,int R){
if(L<=l&&r<=R){
return t[x];
}
tr ret;ret.st();
if(mid<R) ret=ret*query(x<<|,mid+,r,L,R);
if(L<=mid) ret=ret*query(x<<,l,mid,L,R);
return ret;
}
void add(int x,int l,int r,int to,int p,int c){
if(l==r){
if(p) t[x].a[][]+=c;
else t[x].a[][]+=c,t[x].a[][]+=c;
return;
}
if(to<=mid) add(x<<,l,mid,to,p,c);
else if(mid<to) add(x<<|,mid+,r,to,p,c);
pushup(x);
}
int tmp[];
int to[];
int upda(int x,int y){
tmp[]=tmp[]=;
to[]=to[]=;
tmp[]=y-w[x];
w[x]=y;
while(x){
tr anc=A*query(,,n,dfn[top[x]],dfn[nd[top[x]]]);
to[]=anc.a[][],to[]=anc.a[][];
add(,,n,dfn[x],,tmp[]);
add(,,n,dfn[x],,tmp[]);
anc=A*query(,,n,dfn[top[x]],dfn[nd[top[x]]]);
tmp[]=max(anc.a[][],anc.a[][])-max(to[],to[]);
tmp[]=anc.a[][]-to[];
x=fa[top[x]];
}
tr ans=A*query(,,n,dfn[top[]],dfn[nd[top[]]]);
return max(ans.a[][],ans.a[][]);
}
int main(){
scanf("%d%d",&n,&m);
for(reg i=;i<=n;++i)rd(w[i]);
int x,y;
for(reg i=;i<=n-;++i){
rd(x);rd(y);add(x,y);add(y,x);
}
dfs1(,);
dfs2();
build(,,n);
A.a[][]=,A.a[][]=;
A.a[][]=-inf,A.a[][]=-inf;
while(m--){
rd(x);rd(y);
printf("%d\n",upda(x,y));
}
return ;
} }
int main(){
Miracle::main();
return ;
} /*
Author: *Miracle*
Date: 2018/11/12 16:29:49
*/
zkw线段树版：（1500ms）
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define mid ((l+r)>>1)
using namespace std;
typedef long long ll;
il void rd(int &x){
char ch;x=;bool fl=false;
while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
for(x=numb;isdigit(ch=getchar());x=x*+numb);
(fl==true)&&(x=-x);
}
namespace Miracle{
const int N=1e5+;
const int inf=0x3f3f3f3f;
int n,m;
struct node{
int nxt,to;
}e[*N];
int hd[N],cnt;
il void add(int x,int y){
e[++cnt].nxt=hd[x];
e[cnt].to=y;
hd[x]=cnt;
}
struct tr{
int a[][];
void init(int x,int y){//x:ldp0 y:ldp1
a[][]=x,a[][]=x;
a[][]=y,a[][]=-inf;
}
void pre(){
memset(a,-inf,sizeof a);
}
void st(){
a[][]=,a[][]=-inf,a[][]=-inf,a[][]=;
}
tr operator *(const tr& b) const{
tr c;c.pre();
for(reg i=;i<=;++i){
for(reg k=;k<=;++k){
for(reg j=;j<=;++j){
c.a[i][j]=max(c.a[i][j],a[i][k]+b.a[k][j]);
}
}
}return c;
}
void op(){
cout<<left<<setw()<<a[][]<<" "<<left<<setw()<<a[][]<<endl;
cout<<left<<setw()<<a[][]<<" "<<left<<setw()<<a[][]<<endl;
cout<<endl;
}
}s[N],t[*N],A;
int dfn[N],top[N],dfn2[N],fdfn[N],sz[N],dep[N],son[N];
int nd[N];//tot;//num of heavy chain
int fa[N];
int df;
int ldp[N][],dp[N][];
int w[N];
il void dfs1(int x,int d){
dep[x]=d;
sz[x]=;
for(reg i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa[x]) continue;
fa[y]=x;
dfs1(y,d+);
if(sz[y]>sz[son[x]]){
son[x]=y;
}
}
}
il void dfs2(int x){
dfn[x]=++df;fdfn[df]=x;
if(!top[x]) {
top[x]=x;nd[top[x]]=x;
}
if(son[x]) top[son[x]]=top[x],nd[top[x]]=son[x],dfs2(son[x]); dp[x][]=w[x];
ldp[x][]=w[x];
for(reg i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==son[x]||y==fa[x]) continue;
dfs2(y);
ldp[x][]+=max(dp[y][],dp[y][]);
ldp[x][]+=dp[y][];
}
if(son[x]){
dp[x][]=ldp[x][]+dp[son[x]][];
dp[x][]=ldp[x][]+max(dp[son[x]][],dp[son[x]][]);
}
s[x].init(ldp[x][],ldp[x][]);
}
int up;
il void build(){
up=;
for(;up<=n+;up<<=);
for(reg i=up;i<=up+up-;++i){
if(i>=up+&&i<=up+n) t[i]=s[fdfn[i-up]];
else t[i]=A;
}
for(reg i=up-;i;--i) t[i]=t[i<<|]*t[i<<];
}
il void chan(int to,int c0,int c1){
reg i=up+to;
t[i].a[][]+=c0;t[i].a[][]+=c0;
t[i].a[][]+=c1;
for(i>>=;i;i>>=){
t[i]=t[i<<|]*t[i<<];
}
// cout<<" after chan "<<endl;
}
il tr query(int l,int r){
tr le,ri;le.st();ri.st();
for(reg s=up+l-,e=up+r+;s^e^;s>>=,e>>=){
// cout<<s<<" "<<e<<endl;
if(!(s&)) le=t[s^]*le;
if(e&) ri=ri*t[e^];
}
return ri*le;
}
int tmp[];
int to[];
il int upda(int x,int y){
tmp[]=tmp[]=;
to[]=to[]=;
tmp[]=y-w[x];
w[x]=y;
while(x){
//tr anc=A*query(1,1,n,dfn[top[x]],dfn[nd[top[x]]]);
to[]=dp[top[x]][],to[]=dp[top[x]][];
chan(dfn[x],tmp[],tmp[]);
tr anc=A*query(dfn[top[x]],dfn[nd[top[x]]]);
tmp[]=max(anc.a[][],anc.a[][])-max(to[],to[]);
tmp[]=anc.a[][]-to[];
dp[top[x]][]=anc.a[][],dp[top[x]][]=anc.a[][];
x=fa[top[x]];
}
return max(dp[][],dp[][]);
}
int main(){
scanf("%d%d",&n,&m);
for(reg i=;i<=n;++i)rd(w[i]);
int x,y;
for(reg i=;i<=n-;++i){
rd(x);rd(y);add(x,y);add(y,x);
}
dfs1(,);
dfs2();
A.a[][]=,A.a[][]=;
A.a[][]=-inf,A.a[][]=-inf;
build();
while(m--){
rd(x);rd(y);
printf("%d\n",upda(x,y));
}
return ;
} }
int main(){
// freopen("data.in","r",stdin);
// freopen("my.out","w",stdout);
Miracle::main();
return ;
} /*
Author: *Miracle*
Date: 2018/11/12 16:29:49
*/
[学习笔记]动态dp的更多相关文章
- WPF－学习笔记 动态修改控件Margin的值
原文:WPF-学习笔记 动态修改控件Margin的值 举例说明:动态添加一个TextBox到Grid中,并设置它的Margin: TextBox text = new TextBox(); t_gri ...
- Java学习笔记——动态代理
所谓动态,也就是说这个东西是可变的,或者说不是一生下来就有的.提到动态就不得不说静态,静态代理,个人觉得是指一个代理在程序中是事先写好的,不能变的,就像上一篇"Java学习笔记——RMI&q ...
- Angular 学习笔记 (动态组件 & Material Overlay & Dialog 分析)
更新: 2019-11-24 dialog vs router link refer : https://stackoverflow.com/questions/51821766/angular-m ...
- [学习笔记]整体DP
问题: 有一些问题,通常见于二维的DP,另一维记录当前x的信息,但是这一维过大无法开下,O(nm)也无法通过. 但是如果发现,对于x,在第二维的一些区间内,取值都是相同的,并且这样的区间是有限个,就可 ...
- [学习笔记] 数位DP的dfs写法
跟着洛谷日报走,算法习题全都有! 嗯,没错,这次我也是看了洛谷日报的第84期才学会这种算法的,也感谢Mathison大佬,素不相识,却写了一长篇文章来帮助我学习这个算法. 算法思路: 感觉dfs版的数 ...
- 学习笔记-动态树Link-Cut-Tree
--少年你有梦想吗? --少年你听说过安利吗? 安利一个集训队讲解:http://wenku.baidu.com/view/75906f160b4e767f5acfcedb 关于动态树问题,有多种方法 ...
- [WPF学习笔记]动态加载XAML
好久没写Blogs了,现在在看[WPF编程宝典],决定开始重新写博客,和大家一起分享技术. 在编程时我们常希望界面是动态的,可以随时变换而不需要重新编译自己的代码. 以下是动态加载XAML的一个事例代 ...
- 单片机C语言开发学习笔记---动态的数码管
在郭天祥的那本书中,有一个通过按键控制数码管的例子,在运行这个例子的时候,我发现当按键按下的时候,第一位数码管会熄掉,这是为什么呢? 后来在网上找到了原因,当我按下按键不松开的时候,接下来要运行的代码 ...
- EXCEL 2010学习笔记—— 动态图表
今天梳理一下动态图表的相关内容,做一个简单的整理 关键的操作点: 1.插入动态控制器:开发工具->插入->表单控件 对控件进行修改 右键 设置控件格式->单元格链接 用来作为if ...
随机推荐
- 强化记忆之php
php 输出的区分 新手摸索道路,有说不对的地方,还请多多包涵. echo 能够输出一个以上的字符串,也能输出html标签 print 一次只能接受一个字符串(区分与echo),也能输出html标签 ...
- Spring-Boot ☞ ShapeFile文件读写工具类+接口调用
一.项目目录结构树 二.项目启动 三.往指定的shp文件里写内容 (1) json数据[Post] { "name":"test", "path&qu ...
- libpng的使用
zlib 适用于数据压缩的函式库,由Jean-loup Gailly (负责compression)和 Mark Adler (负责decompression)开发. zlib被设计成一个免费的.通用 ...
- 算法竞赛入门经典-1.5.4 Q&A
这小节考察实践能力,要求在不要查书.不要网上找答案,自己用实验的方法解决以下五个问题: 做这五道题时,好几道都没思路,违反了规则到网上找了一圈,居然没找到答案,于是打算写这篇博客.不知是否有更好的实践 ...
- Python3爬虫（十二） 爬虫性能
Infi-chu: http://www.cnblogs.com/Infi-chu/ 一.简单的循环串行一个一个循环,耗时是最长的,是所有的时间综合 import requests url_list ...
- SKIP(插入空行)
WRITE 'This is the 1st line'. SKIP. WRITE 'This is the 2nd line'. 跳转至某一行 SKIP TO LINE line_number. 插 ...
- Java线程和多线程（九）——死锁
Java中的死锁指的就是一种多于两个线程永远阻塞的特殊状况.Java中的死锁状态至少需要多于两个线程以及资源的时候才会产生.这里,我写了一个产生死锁的程序,并且讲下如何分析死锁. 首先来看一下产生死锁 ...
- 初步学习pg_control文件之九
接前文,初步学习pg_control文件之八 来看这个: pg_time_t time; /* time stamp of last pg_control update */ 当初初始化的时候,是这样 ...
- 雷哥带你走进Javascript
javascript复习笔记--------------------------------------------1.概念2.面向对象思想3.作用认识4.引入方式5.执行顺序 变量 1)声明方式 x ...
- 利尔达NB-IOT的PSM和eDRX低功耗模式笔记
1. NB-IOT的技术优势,广覆盖,NB-IOT与GPRS和LTE相比较,最大链路预算提升了20dB,相当于提升了100倍,即使在地车车库.地下室.地下管道等普通无线网络信号难以到达的地方也容易覆盖 ...